トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

有効次元数

データサイエンス では、 変数の数（表データの列の数）と、次元の数を同じように考えることが多いです。 例えば、変数がたくさんある表データは、「 高次元のデータ 」と呼んでいることがあります。

ところで、現実のデータでは、一見すると、変数がたくさんあっても、分析の中で注意しなければいけない変数の特徴は少ししかないことがあります。

「たくさん」が「少し」になる主な理由は、下記の２つです。

このページのタイトルの「有効次元数」というのは、分析の中で意味のある次元の数です。 これがわかると、データ分析の見通しが良くなりますし、計算時間を短くすることができます。

なお、「有効次元数」は、筆者の造語です。 世の中に同じ意味の言葉がすでにあれば、差し替えますが、ないようなので、さしあたって付けました。

表データの有効次元数

主成分分析 を使うと、複数の変数が整理されて、主成分という変数に変換されます。 この時、元の変数が10個あると、主成分も10個まで作ることができますが、 第１主成分、第２主成分、という順に、データの特徴が優先順位をつけてまとめられています。 例えば、多重共線性があると、第３主成分まででデータの特徴がほぼ表現できていて、第４主成分以降は非常に小さな数値になります。 この時は有効次元数は３と考えることができます。

有効次元数がいくつになるのかの判断は、累積寄与率が1に近くなっているかをみるか、主成分の標準偏差が非常に小さな数値かをみるか、の２種類の方法があります。

特徴量エンジニアリング としては、新しい変数を作る時に、有効次元数を使います。 中間層を使った解析 でも使います。

なお、有効次元数というのは、データの大きな変化が何次元で表されるかという指標です。 小さな変化の方が重要な分析では、有効次元数の範囲だけで主成分を見ていれば良いわけではないです。

例

下の ヒートマップ は、longleyというRのサンプルデータを 標準化 して作ったものになります。 上から下にかけて、値が大きくなっている変数が５つあって、それとは様子の違う変数が２種類、１つずつあります。 そのため、変化の仕方としては３種類あります。
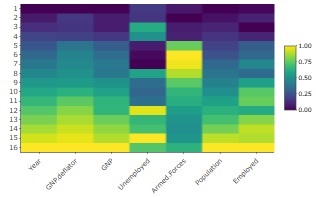
R-EDA1

これの主成分分析の結果が下記になります。 累積寄与率（Cumulative Proportion）が第３主成分で99%を超えていることから、上記の「３種類」というヒートマップの結果と一致します。
R-EDA1

この例の場合は、有効次元数は３と考えます。

作られた主成分の ヒートマップ が下になります。
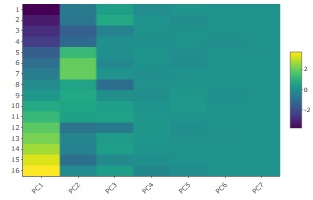
R-EDA1

PC1の値の幅が一番大きく、PC2、PC3までは、濃淡がわかりやすいですが、PC4からPC7は濃淡がわかりにくいです。 このグラフからも、有効次元数は３と考えられます。

距離行列のデータの有効次元数

距離行列のデータがスタートになっている場合も、有効次元数はあります。 距離行列自体は、多次元を２次元の形で表していますが、その背後にあるデータの特徴は３次元以上である場合があります。

多次元尺度構成法 を使うと、距離行列が座標データに変換できるのですが、無理なくサンプルが多次元空間に配置される次元数が、有効次元数と考えられます。

この方法は、 一対評価 で得たデータがA-A型の時に、 A-A型の分析 方法として使えます。 類似度（近いほど大きい）のデータの場合は、距離（近いほど小さい）のデータに変換すると使えます。

例１（longley)

上記のlongleyについて、標準化をしてから距離行列を作り、最大７次元で 多次元尺度構成法 をした結果の ヒートマップ が下になります。
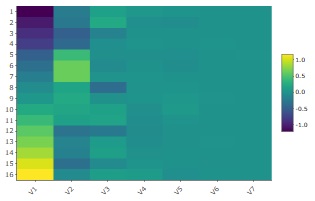
R-EDA1

V1の値の幅が一番大きく、V2、V3までは、濃淡がわかりやすいですが、V4からV7は濃淡がわかりにくいです。 そのため、この例の場合は、有効次元数は３と考えられます。

ちなみに、このヒートマップは主成分分析の結果と見た目がとても似ていますが、例えば、色分けの範囲が違っています。

例２（UScitiesD)

UScitiesDというRのサンプルデータは、米国の都市間の距離行列のデータです。
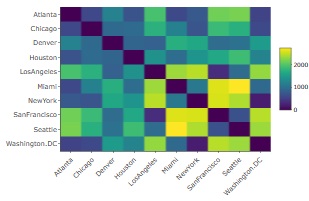
R-EDA1

最大５次元で 多次元尺度構成法 をした結果の ヒートマップ が下になります。
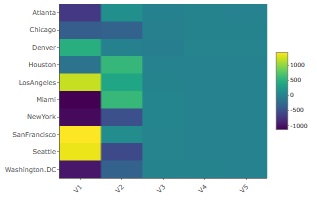
R-EDA1

V1、V2までは、濃淡がわかりやすいですが、V3からV5はほぼ一定値です。 そのため、この例の場合は、有効次元数は２と考えられます。 米国の都市だけなら、２次元（平面）で配置を表現できるという意味なので、一般的な認識と合っている結果が出ました。

例３（野菜の分類）

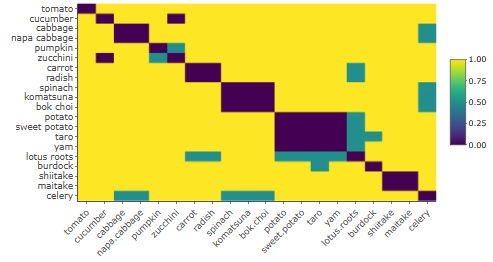
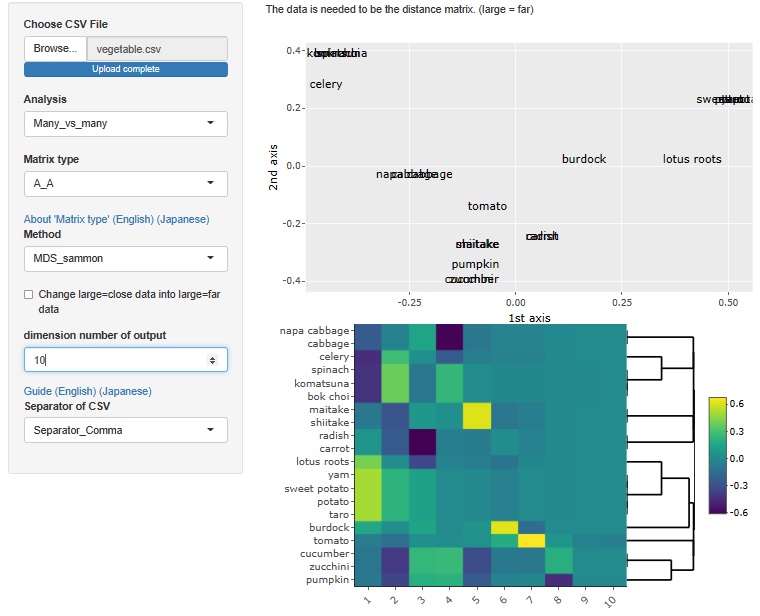
野菜を「似ている＝0、似ていない＝1、判断迷う=0.5」で、筆者が作った距離行列のデータです。 正確には、距離０のサンプル同士があると多次元尺度構成法でエラーになるため、少し乱数を足して、距離がピッタリ０にならないようにしています。
R-EDA1

最大10次元で 多次元尺度構成法 をした結果の ヒートマップ が下になります。
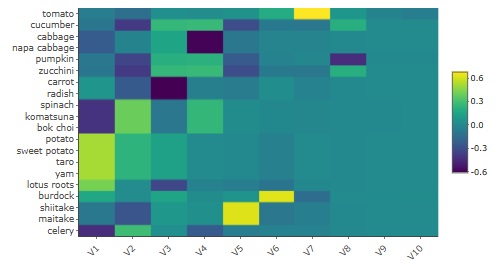
R-EDA1

V1、V8までは、濃淡がわかりやすいですが、V9、V10はほぼ一定値です。 そのため、この例の場合は、有効次元数は８と考えられます。 大きく分けると８種類の野菜があると、筆者が認識していることがわかります。

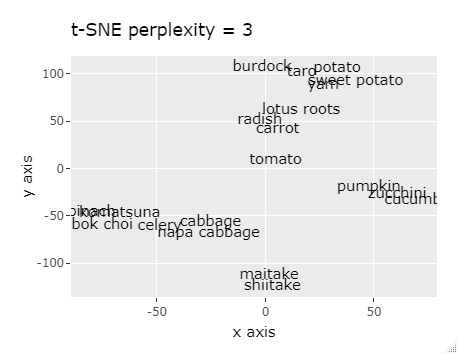
ちなみに、上記の距離行列のデータを t-SNE の入力データにすると、２次元マップ上に似ているものが集まるように配置されるのですが、 あまりはっきりと分かれません。　下記以外に、perplexityを変えても似たり寄ったりの結果でした。 このデータではt-SNEは良くないです。
R-EDA1

ソフトウェア

R-EDA1 では、上記の分析ができるようになっています。

R-EDA1



順路 次は 予測とシミュレーション

データサイエンス教室