「高次元」というのは相対的な言い方なので、「〇次元以上は高次元」と言うことはないのですが、
データの列が比較的多い場合を、このサイトでは「高次元」と呼んでいます。
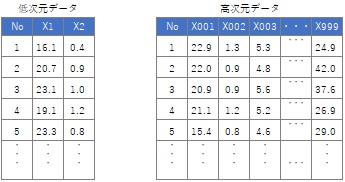
ちなみに、「高次元」は「多次元」と呼ばれることはありますが、「低次元」を「少次元」と呼ぶことはないようです。 また、「高次元」は「多変量」や「多変数」と呼ばれることもあります。
高次元のデータであることと、データの列が多いことは、必ずしも同じではないのですが、混同されることがあります。 区別して意識していると、 データサイエンス の幅が広がります。
この部分の内容は、 時空間のデータ のページとかぶるところがあります。
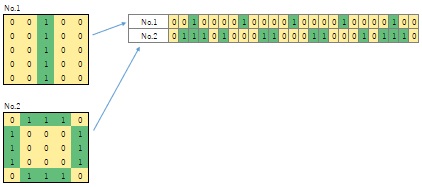
平面の情報をデータにする時には、まず、下図のNo.1やNo.2のようになります。 それぞれが冒頭の高次元データのような形になっています。 しかし、このままでは、平面同士の違いを調べたり分類をするための 多変量解析 などの手法が使えません。
そこで、縦方向や横方向で短冊状にしてそれを１本につなげた形にすると、様々な手法が使えるようになります。
この場合の次元とは、それぞれの格子の座標になります。
列の順番には意味がある点がポイントです。
一般的な
多変量解析
の手法では、列の順番は気にしないアルゴリズムになっていますので、近い格子の関係が考慮されません。
平面のデータの代表的なものは、画像と思います。 筆者の場合は、シリコンウェハーを格子状に区分けして検査したデータを扱っていた時期がありますが、そういった平面のデータもあります。
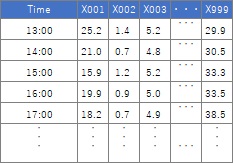
時系列データの場合は、高次元データの形が２種類あります。
１つ目は、冒頭の高次元データの形に最初からなっているデータです。
同じ行のデータは、同じ時刻のデータになっています。
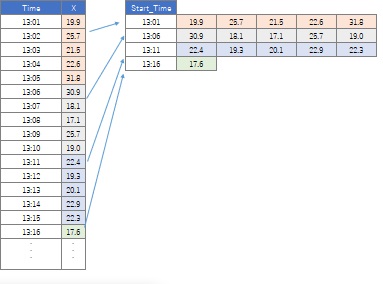
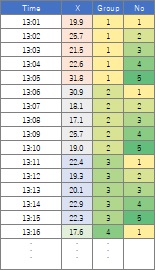
２つ目は、元のデータは１次元のデータになっている場合です。
時系列のデータを区間で区切って、並べなおすと、高次元データの形になります。 ひとつの区間が冒頭のデータの１行になります。 この場合の次元とは、区切りの最初からの順番になります。 列の順番には意味があります。
２つ目の形ですが、工場のデータでは、区間が決まった長さにならないことがよくあります。
そのため、高次元であるだけでなく、次元数が行ごとに異なることになり、扱いが難しいデータになります。
2つ目のデータの形の行と列を入れ替えたタイプのデータを、
このサイトでは、
1.5次データ
と呼んでいます。
折れ線グラフで分析したい時は、1.5次データの形にする必要があります。
なお、
1.5次データの形では高次元のデータとして扱えません。
高次元のデータになる前の状態でもあるのですが、
メタ知識のデータの作成
の方法を使って、３次元のデータを作ることができます。
この形式にすると、次元数が行ごとに異なることはないので便利です。
順路
次は
お金のデータ
