個々のサンプルの因果推論 をRで実施する時の例です。
変数間の因果推論の方法の応用としては、 Rによる変数の類似度の分析 や Rによる決定木 で調べる方法があります。
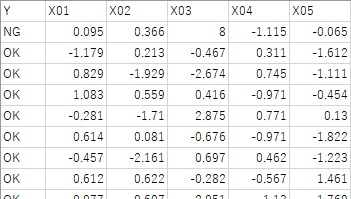
以下の例で使っているサンプルデータでは、X01からX05まであります。
１行目が因果推論をしたいサンプルになっていて、Yの値は「NG」となっています。X03に比較的大きな値が入っています。
１行目以外は、Yの値は「OK」となっています。
調べたいサンプルが複数あり、それらのサンプルは特徴が共通していると考えている想定している場合は、 例えば、異常のサンプルのグループのYを「NG」として、その他を「OK」とすれば、複数のサンプルをまとめて分析できます。
Rによる決定木 のページは、決定木の一般的なデータ分析での使い方になっているのですが、 個々のサンプルの因果推論に使う時は、少しアレンジする必要があります。
まず、個々のサンプルの因果推論では、調べたいサンプルは、１個から数個の事が多いので、葉に含まれる最小サンプル数がデフォルトのままだと、 木が分岐せずに調べられないです。そこで、最小サンプル数を変更します。 また、ランダムフォレストでは多数の木を作りますが、その木の中に調べたいサンプルが含まれない可能性があるので、一般的なランダムフォレストは向かないです。 ランダムフォレストにするなら、変数のランダムサンプリングのみにして、サンプルのランダムサンプリングはしない方が良いです。
以下は、rpartの実施例になります。
setwd("C:/Rtest") # 作業用ディレクトリを変更
library(partykit) # ライブラリを読み込み
library(rpart) # ライブラリを読み込み
Data <- read.csv("Data.csv", header=T) # データを読み込み
treeModel <- rpart(Y ~ ., data = Data,control = rpart.control(minsplit = 1))# rpartを実行。最小サンプル数は1
plot(as.party(treeModel)) # グラフにする。
X03がこのサンプルの特徴になっていることが、導き出せました。
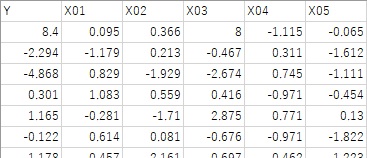
以下の例で使っているサンプルデータでは、X01からX05まであり、Yは、X01、X02、X03の線形和になっていて、X04とX05はYに無関係なデータになっています。
１行目が因果推論をしたいサンプルになっていて、X03に比較的大きな値が入っています。
SHAPを計算する方法は、１個のサンプルだけを調べる方法になっています。 複数を調べたい場合は、同じ作業を繰り返して、出てきた結果を集計することになります。
library(iml) # ライブラリを読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- Data
Data1$Y <- NULL # Yの列を消す
library(randomForest)# ライブラリを読み込み
DataModel = randomForest(Y ~ ., data = Data)# モデルを作成
predictor = Predictor$new(DataModel, data = Data1, y = Data$Y)# モデルを作成
shapley = Shapley$new(predictor, x.interest = Data1[1,])# Shap値を計算（１行目のサンプルの場合）
shapley$plot()# グラフにする
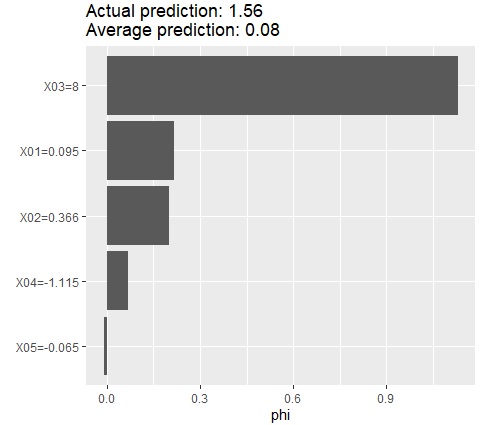
X03がこのサンプルの特徴になっていることが、導き出せました。
上記の方法について、モデルを変えたい場合は、真ん中あたりの２行を書き換えます。 例えば、重回帰分析（一般化線形モデル）の場合は以下の２行を入れます。
library(MASS)# ライブラリを読み込み
DataModel = glm(Y ~ ., data=Data, family= gaussian(link = "identity"))# モデルを作成
