 Rによるデータ分析
Rによるデータ分析
 Rによるデータ分析
Rによるデータ分析
LiNGAM のRによる実施例です。
モデル式の係数を調べる方法です。
pcalgは、LiNGAMのためのパッケージです。
ここでは、以下の式で作ったデータを使っています。
eのところは、一様分布の乱数を使っています。
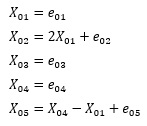
library(pcalg) #ライブラリの読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
Str <- lingam(Data)$Bpruned # LiNGAM
rownames(Str) <- colnames(Data) # 行名を追記
colnames(Str) <- colnames(Data) # 列名を追記
Str
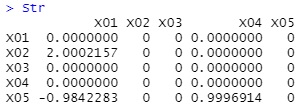
データを作った時の係数とほぼ同じ値が求まりました。
参考文献のところにありますが、pcalgを使うには、CRANにはないライブラリが先にインストールされている必要があります。 それが原因で、pcalgが使えないことがあります。
そこで、pcalgを使わずにLiNGAMを実行するためのコードが、下記になります。 メインのところは、ChatGPTで作っています。DirectLiNGAMを、Shimizu氏の2011年の論文に沿って作っているそうです。
R-EDA1 でも、このコードを使っています。
下記の実施例のように、pcalgと、ほぼ同じ結果になることは、確認しています。
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
### ここからpcalgと異なる部分 ###
independence_score <- function(x, r) {
abs(cor(tanh(x), r))
}
direct_lingam <- function(X) {# ここからpcalgのlingam関数に相当する関数を作成
n <- nrow(X)
p <- ncol(X)
vars <- colnames(X)
causal_order <- c()
B <- matrix(0, p, p)
colnames(B) <- rownames(B) <- vars
X_work <- X
var_index <- 1:p
while (ncol(X_work) > 1) {
scores <- rep(0, ncol(X_work))
for (j in 1:ncol(X_work)) {
xj <- X_work[, j]
others <- X_work[, -j, drop = FALSE]
sc <- 0
for (k in 1:ncol(others)) {
fit <- lm(others[, k] ~ xj)
r <- resid(fit)
sc <- sc + independence_score(xj, r)
}
scores[j] <- sc
}
root <- which.min(scores)
root_name <- colnames(X_work)[root]
if (ncol(X_work) > 1) {
for (k in 1:ncol(X_work)) {
if (k != root) {
fit <- lm(X_work[, k] ~ X_work[, root])
B[var_index[k], var_index[root]] <- coef(fit)[2]
X_work[, k] <- resid(fit)
}
}
}
X_work <- X_work[, -root, drop = FALSE]
var_index <- var_index[-root]
}
list(
adjacency_matrix = B
)
}
Str <- direct_lingam(Data)$adjacency_matrix# ここはpcalgのlingam関数を使う部分に相当
### ここまでpcalgと異なる部分 ###
Str

重回帰分析 で、各変数の影響の大きさを調べたい時は、単純に回帰式の各変数の係数を比べることは間違いで、偏回帰係数を比べます。 偏回帰係数は、各変数を 標準化 してから、重回帰分析をして求まる係数になります。
因果関係の分析にLiNGAMを使う場合も、単純にLiNGAMの出力を使おうとすると、同じ間違いが起きます。 ここでも標準化をしてから、LiNGAMを実行することにします。
そして、この係数を影響の大きさを表す数値として、ネットワーク構造の太さに使います。
#のついた3行は、#を消せば、データの前処理に標準化をします。 筆者の経験上、標準化をすると、矢印の方向が間違った結果になることが多いです。
library(pcalg) #ライブラリの読み込み
library(igraph) #ライブラリの読み込み
setwd("C:/Rtest") # 作業用ディレクトリを変更
Data <- read.csv("Data.csv", header=T) # データを読み込み
#for (i in 1:ncol(Data)) {
# Data[,i] <- (Data[,i] - mean(Data[,i]))/sd(Data[,i]) #データを標準化
#}
Str <- lingam(Data)$Bpruned # LiNGAM
rownames(Str) <- colnames(Data) # 行名を追記
colnames(Str) <- colnames(Data) # 列名を追記
GM2 <- t(abs(Str)) # 絶対値にして転置する
GM3 <- GM2*5/max(GM2) # 値を適度な大きさにする
GM4 <- graph.adjacency(GM3,weighted=T, mode = "directed") # グラフ用のデータを作成
plot(GM4, edge.width=E(GM4)$weight) # グラフを作成
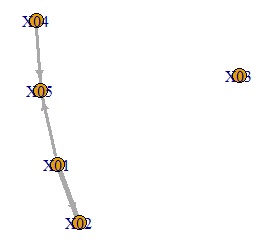
矢印の元側の変数に誤差が加わって、矢印の先の変数になっていることを表しているグラフができます。
行列の分解 の一種に、「シュール分解」と呼ばれるものがあります。
シュール分解では、上三角行列が求まります。
LiNGAMでは、非巡回有向グラフを、三角行列で表せるところがポイントになっているので、 シュール分解を使うLiNGAMのアルゴリズムができるのではないかと思ったのですが、 筆者は、うまく行きませんでした。
ちなみに、Rでは、分解したい行列がAの時に、以下のようにして、上三角行列が求まります。
library(expm)
Schur(A)$T
筆者が試したところ、上三角行列に近い行列が求まるのですが、完ぺきな上三角行列にはなりませんでした。
「つくりながら学ぶ! Pythonによる因果分析 因果推論・因果探索の実践入門」 小川雄太郎 著 マイナビ出版 2020
LiNGAMの実装は、この本を参考にさせていただきました。
「「統計的因果探索」の一部を動かしてみた」
山川信之氏のブログです。
pcalgをインストールする前に、別のライブラリのインストールが必要なことが書かれています。
また、LiNGAMの簡単な実施例もあります。
https://techblog.nhn-techorus.com/archives/13805
の3つを紹介しています

