LiNGAM は、「非正規分布ならできる」という説明がされる手法です。 そこで、それを確かめてみたのがこのページです。
始めに結論を書きます。
筆者としては、意外な結論になっています。 実務で使うことを考えると、うれしい結論です。
検証するモデルの式は下記です。
LiNGAMの出力の行列の中に、「2」、「1」、「-1」が１回ずつ出て来て、それ以外が全部「0」だったら、正解になります。
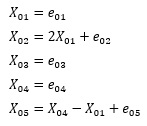
eのところに、指定した分布になる乱数が入ります。 5つのeは、それぞれが独立しています。
今回試した分布は、正規分布、ロジスティック分布、コーシー分布、一様分布、指数分布、対数正規分布です。 それぞれを、rnorm(10000)、rlogis(10000)、rcauchy(10000)、runif(10000)、rexp(10000)、rlnorm(10000)というコードで、作ります。 この表記からわかるように、それぞれの分布のパラメータは、デフォルトのまま使います。 （パラメータを設定しなくても、エラーが出ない分布を選んでいます。）
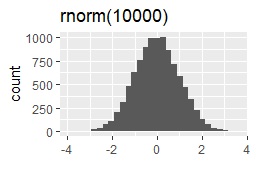
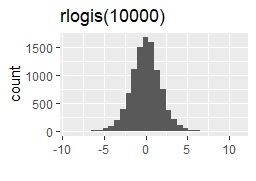
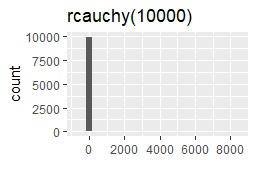
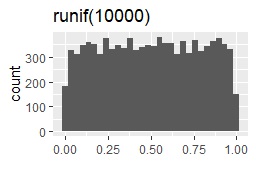
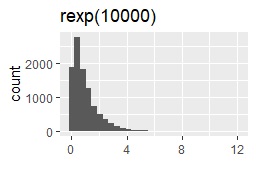
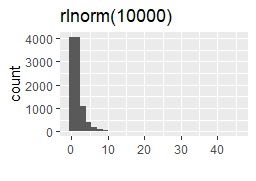
コードは下記です。 分布によって、下記の「rnorm(10000)」の部分を書き換えます。
e01 <- rnorm(10000)
e02 <- rnorm(10000)
e03 <- rnorm(10000)
e04 <- rnorm(10000)
e05 <- rnorm(10000)
X01 <- e01
X02 <- 2 * X01 + e02
X03 <- e03
X04 <- e04
X05 <- X04 - X01 + e05
Data <- as.data.frame(cbind(X01,X02,X03,X04,X05))
コードは下記です。 「RによるLiNGAM のページとほぼ同じです。
pcalgを使うコードが下記です。
library(pcalg)
Str <- lingam(Data)$Bpruned # LiNGAMの実行
rownames(Str) <- colnames(Data)
colnames(Str) <- colnames(Data)
round(Str,1) # 小数点第１位まで出力
pcalgの部分も自作のコードが下記です。
上記のコードの最初の２行が書き変わっています。
library(fastICA)
n <- ncol(Data)
fICA <- fastICA(Data, n)
K <- fICA$K
W <- fICA$W
tKW <- t(K %*% W)
MintKW <- tKW
MinSum <- sum(diag(1/abs(tKW)))
for (i in 1:10000) {
tKW2 <- tKW[order(sample(tKW,n)),]
SumdiagRabstKW <- sum(diag(1/abs(tKW2)))
if(MinSum > SumdiagRabstKW){
MinSum <- SumdiagRabstKW
MintKW <- tKW2
}
}
MintKW2 <- MintKW
for (i in 1:n) {
MintKW2[i,] <- MintKW2[i,]/MintKW2[i,i]
}
Str <- MintKW2
diag(Str) <- 0
rownames(Str) <- colnames(Data)
colnames(Str) <- colnames(Data)
round(Str,1)
まず、正規分布以外の結果です。
どの分布でも、正解になりました。
次に正規分布の時の結果が下図になります。
下図の３つの結果は、何回も試した中の３つの例になります。
一番左の時だけが正解で、他の２つは、「2」、「1」、「-1」のうちの１つが間違いになっています。
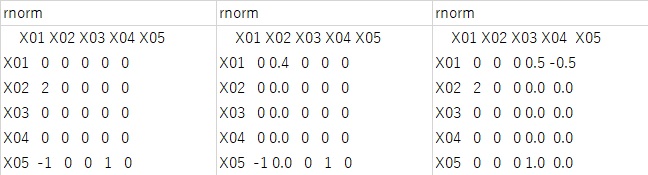
筆者が試した感じだと、正規分布の場合、20〜30回する中の１回くらいの割合で、間違った答えになりました。
この現象は、まったく同じデータセットでも、「lingam」のコードを繰り返すだけで起きるので、 おそらくlingamの中のICAの計算に含まれているランダム性の部分が影響しているようです。
結論として、分布がわかっている、わかっていないに関わらず、10回くらい試してみて何回も再現する結果を採用する使い方にすれば、 LiNGAMは正規分布の時でも役に立つ方法と考えられます。
正規分布の時は、全然ダメでした。
その他の分布の時は、0.1くらいの誤差があるものの、どれも正解と言える結果になりました。
上記の実験は、サンプル数が10000個です。
これを100個にして、pcalgのケースを実行すると下図の結果になります。
でたらめな数字ではなく、ある程度正解に近い結果になっているものの、0になって欲しくないところが0になっていることもあります。
数百個程度のサンプル数の時には、正解では0にならないところが0になっている可能性をリスクとして考えておくと良いようです。
「CRAN」
pcalgのマニュアルです。
https://cran.r-project.org/web/packages/pcalg/pcalg.pdf
LINGAMには、fastICAが使われていることが書かれています。
順路
次は
LiNGAMが正規分布でも有効な理由
