「Model1、Model2の２つがあって、持っているデータがどちらなのかを知りたい時に、 例えば一様分布の時は、散布図を作ると明らかに違うので、識別ができる。」という説明がされるのが一般的です。 下の例では、左側がModel1で、右側がModel2であることは、グラフから推測できます。
LiNGAMが有効な分布 では、「正規分布でもできる」という結論になっています。 しかし、「LiNGAM」という名前の、「NG」は、「Non-Gaussian（非正規分布）」なので、 「正規分布でもできる」というのは変な話です。
できる理由の考察がこのページです。
なお、このページの内容は、筆者の仮説になります。 筆者自身は正しいと思っていますが、今後、間違いなことがわかれば、修正します。 既に同じ内容の研究があったり、この仮説が間違いなことを示す資料があるかもしれませんが、筆者の知る限りでは見つかっていません。
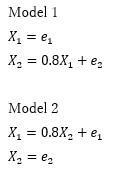
「Model1、Model2の２つがあって、持っているデータがどちらなのかを知りたい時に、
例えば一様分布の時は、散布図を作ると明らかに違うので、識別ができる。」という説明がされるのが一般的です。
下の例では、左側がModel1で、右側がModel2であることは、グラフから推測できます。
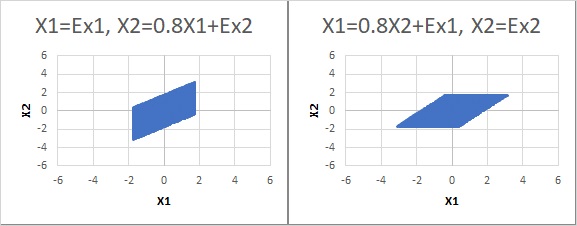
「一方、正規分布だと、同じような分布になるので、識別ができない。だから、LiNGAMは非正規分布に使える理論」という説明もされます。
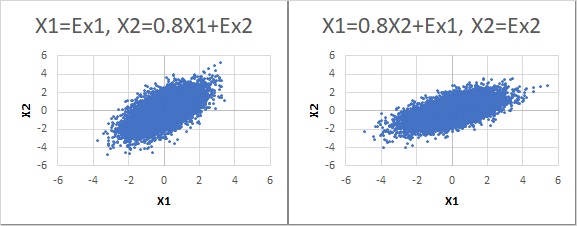
「正規分布だと識別できない」という説明は、グラフの見た目に対して行われています。
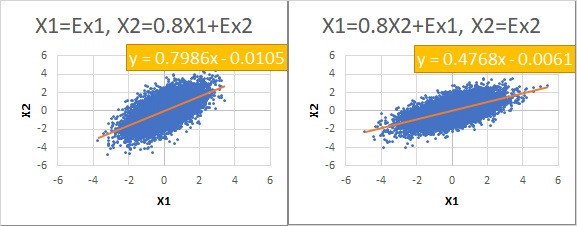
ところで、正規分布の時の２つの散布図について、それぞれ回帰式を求めてみます。
すると、左側の方は、傾きの係数が約0.8になり、右側の方は、約0.5になりました。
「0.8」という同じ数字が求まったのは左側だけです。
Model1の式で作られているデータを
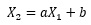
という式に当てはめる時は、Model1の式の形と、この式の形が対応しているので、aが0.8くらいに求まります。
一方、Model2の式で作られているデータは、
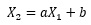
という式に当てはめる時は、式の形が対応しません。
対応しない部分のつじつま合わせが、aの計算値に含まれてくるので、この場合は、aが0.5くらいになっています。
ちなみに、 回帰分析への測定誤差の影響 にも、似た話があります。
同様にして、Model1の式で作られているデータを
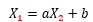
という式に当てはめる時は、対応しない部分のつじつま合わせが必要になって来て、aが0.5くらいになります。
つじつま合わせの効果は、「aが小さくなる」という形で表れます。
筆者が調べてみたところ、eの標準偏差が1になる場合は、 つじつま合わせの効果は、「aが小さくなる」と決まっていました。 筆者が、手法を試す時は、eの標準偏差が1なので、この条件に当てはまっていました。
下の図は、eが1の場合に、Model1で作ったaを横軸にして、2つのモデルのaの差を縦軸にしたものです。
差の値がプラスしかないので、Model1の場合が必ずaが大きいことがわかります。
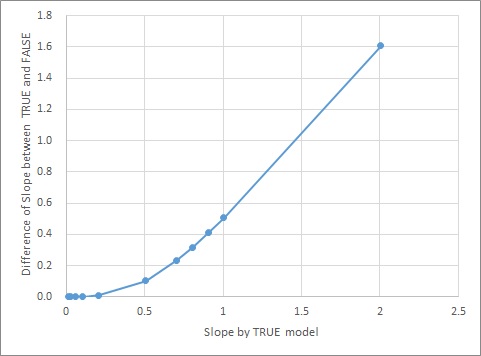
そのため、元々のデータが、Model1なのか、Model2なのかがわからない場合、aの絶対値が大きく求まる方が、モデル式として推定でます。
元々のデータが、Model1だと、
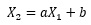
の時と、
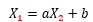
の時を比べると、前者の方がaの絶対値が大きく求まるので、正解は、前者ということになります。
LiNGAMのアルゴリズムは、絶対値の大きい方を推定式の係数として採用して、もう片方を０にします。 そのため、正規分布でも正解の構造が推定できるアルゴリズムになっていると考えられます。
「因果探索 基本から最近の発展までを概説」
清水先生によるLiNGAMの解説です。
https://www.slideshare.net/sshimizu2006/ss-60015497
p.30のところの、正規分布と一様分布の比較の話は、LiNGAMの他の方の解説でも見受けられます。例えば、下記があります。
LiNGAMで因果グラフを探索してみる with R
A→Bなのか、B→Aなのかをデータから見抜くことはできるだろうか？（LiNGAMのシミュレーションをしてみた）
順路
次は
LiNGAMの限界
