LiNGAM は、画期的な方法ですが、限界もあります。 筆者が使っていて気付いたものをまとめてみました。
なお、「LiNGAM」という名前の、「NG」は、「Non-Gaussian（非正規分布）」なので、 「正規分布が使えないのが限界」と思いたくなりますが、その点については、 LiNGAMが有効な分布 に、そうでもないことをまとめています。
このページの例は、RのpcalgというライブラリでLiNGAMをしている時の話になります。 どんなLiNGAMでも、同じ特徴があるのかどうかまでは、まだわからないでいます。
このページの限界は、非正規分布の一様分布で確認していますので、正規分布かどうかには関係のないLiNGAMの限界です。
まず、LiNGAMが限界にはなっていない時の例です。
誤差項のe1、e2が一様乱数の時、LiNGAMは下記の結果になります。
左側が、検証用のデータを作る時の式で、右側が、LiNGAMの結果です。 係数の「2」が「2.011809」として、だいたい合っている数字が求まっています。
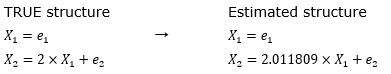
なお、この計算をする時に、e1とe2では、
runif(10000)
というRの式を使って、10000個の一様分布の乱数を求めて使っています。
LiNGAMの手法を試してみる時は、誤差項のばらつきの大きさは、だいたい同じものにしてみることが、世の中では多いようです。 筆者も始めはそうした例を中心に試していました。
ところが、誤差項のばらつきの大きさが、かなり違う時には、結果が想定通りにならないことがあります。
e2のばらつきが、e1の100倍ある時の例です。
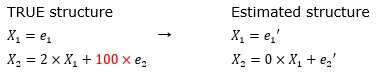
係数の「2」が求まりません。 推定された式は、「X1とX2は独立している」という意味になります。
e2の誤差項の大きさが大きいために、「0（X1の影響はなし）」という推定になっています。
上記の例ですが、X1の係数がある程度大きいと、誤差項の大きさに埋もれなくなるため、欲しい係数が求まります。
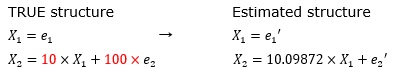
e2のばらつきが、e1の0.01（1/100）倍ある時の例です。
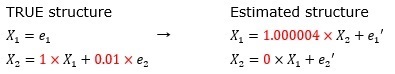
e2の誤差項が小さ過ぎると、誤差項がない状態と区別できなくなり、係数が０ではない場所が特定できなくなっています。
上記の例ですが、X1の係数がある程度大きいと、欲しい係数が求まります。
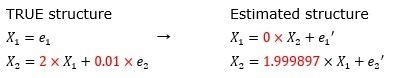
係数が「2」ではなく、もっと小さくなると、求まらなくなります。
係数が「0.02」の例です。
e2の誤差項の大きさが大きいために、「0（X1の影響はなし）」という推定になっています。
上記の例ですが、誤差項が相対的に小さくなると、誤差項の大きさに埋もれなくなるため、欲しい係数が求まります。
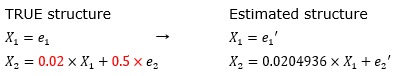
上記の「係数が極端に小さくても、大丈夫な時」では、「誤差項が相対的に小さい時は、大丈夫」としていますが、 誤差項が上記の例よりもさらに小さくなると、新たな限界になります。
誤差項の係数を上記の「0.5」から「0.2」に変えています。
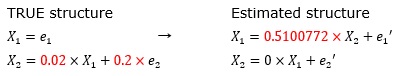
この例の時は、係数が0になってしまうだけでなく、別の係数で0になって欲しいところが、0ではなくなってしまいました。
順路
次は
LiNGAMによる変数の関係の探索
