 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
LiNGAM は、構造モデルの係数を求める方法なので、 変数の類似度の分析 に使う時には、ひと工夫必要になります。
標準化や正規化 が、その工夫になります。
この工夫は、 LiNGAMの限界 になっているデータでも間違えずに分析するための工夫として使えます。
LiNGAMの限界 にある話のうち、「片方の誤差が極端に大きい時」、「片方の誤差が極端に小さい時」、「係数が極端に小さい時」については、 標準化や正規化 をしても、相対的な大きさの関係は変わらないので、効果はありません。
「係数が極端に小さくて、片方の誤差が極端に小さい時」については、
標準化や正規化
をすると、結果が変わります。
「係数が極端に小さくて、片方の誤差が極端に小さい時」で困るのは、0であって欲しいところが0でなくなり、
0になって欲しくないところが0になることでした。
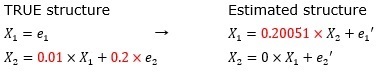
しかし、例えば、LiNGAMの前に各変数を標準化しておくと、結果は下記になります。
「0.01」という数字が求まる訳ではないのですが、少なくとも、式の構造は間違えないで済みます。
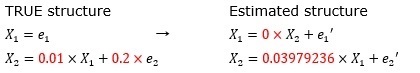
唐突ですが、LiNGAMの結果として、下記の式が求まったとします。
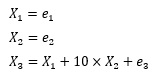
係数の大きさを見ると、X3に対して、X1が1で、X2が10です。 しかし、この情報から「X2の方がX3との関係が強い(相関が大きい)」という結論を出すのは間違いになります。
X3を縦軸にして、X1とX2を横軸にすると、下のグラフだったとしても、LiNGAMで上記の結果になることがあります。
このグラフを見ると、X3と関係が強いのは、X1の方です。
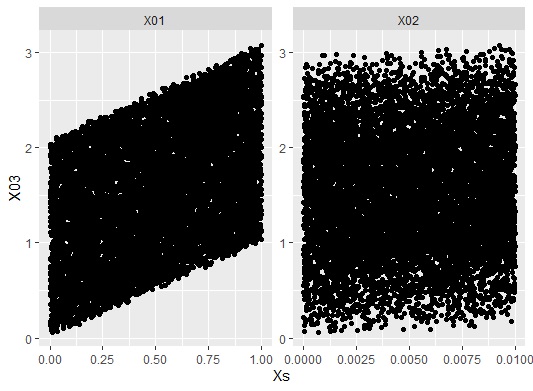
この現象は、e1、e2、e3のばらつきの大きさが極端に違うと起こります。
重回帰分析 をする時に、単位の異なる変数同士について、目的変数Yへの影響度を見たい場合、単純に重回帰分析をした時の各変数の係数ではなく、 標準偏回帰係数を見ないと、間違いになります。 係数の単位がそれぞれ異なり、単位の異なる数字を比較することになるためです。
標準偏回帰係数というのは、各変数を標準化してから重回帰分析をすると求まる係数ですが、これを使うと、単位が同じになるため、 上記の間違いがなくなります。
これと同じことが、LiNGAMを使って、変数の関係の強さを見る時にも起きます。 そのため、変数の前処理として、 標準化や正規化 をする必要があります。
標準化や正規化 をしておくと、係数の数字がその変数の影響度を表す数字として使えるようになります。
上記の例の場合は、標準化をしてからLiNGAMをすると、下の結果になります。
X1の係数の方が、X2の係数の10倍あり、関係の強さが係数の大きさで見えるようになっています。
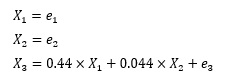
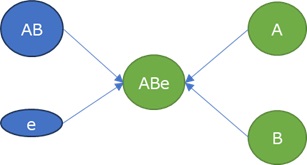
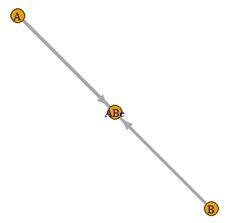
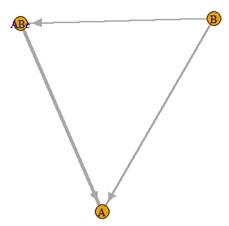
下の例の場合、一番左がデータの構造、真ん中が標準化なし、一番右が標準化ありです。
標準化ありは、おかしな結果になっています。
標準化をすると、変数間の式の関係が崩れるので、このような事が起きるようです。
この例の場合は、標準化はしない方が正しいです。
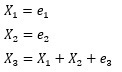
という構造式になっている変数があったとします。
この場合、e1、e2、e3の誤差項が、すべて同じくらいの範囲でばらつく時は、LiNGAMで構造式を正しく推定できるので、 変数の関係性を正しく分析できます。
ところが、e3だけが極端に小さい場合、
以下の3つの式が同じなことと似た状態になるため、LiNGAMで構造を特定することができなくなります。
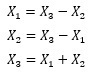
この問題は、 標準化や正規化 でも、解決しないです。
ただし、「変数の関係は足し算しか成り立たないはず」という前提が置ける場合は、 「マイナスの符号は、認めない」という条件をアルゴリズムに付ければ、解決するかもしれません。
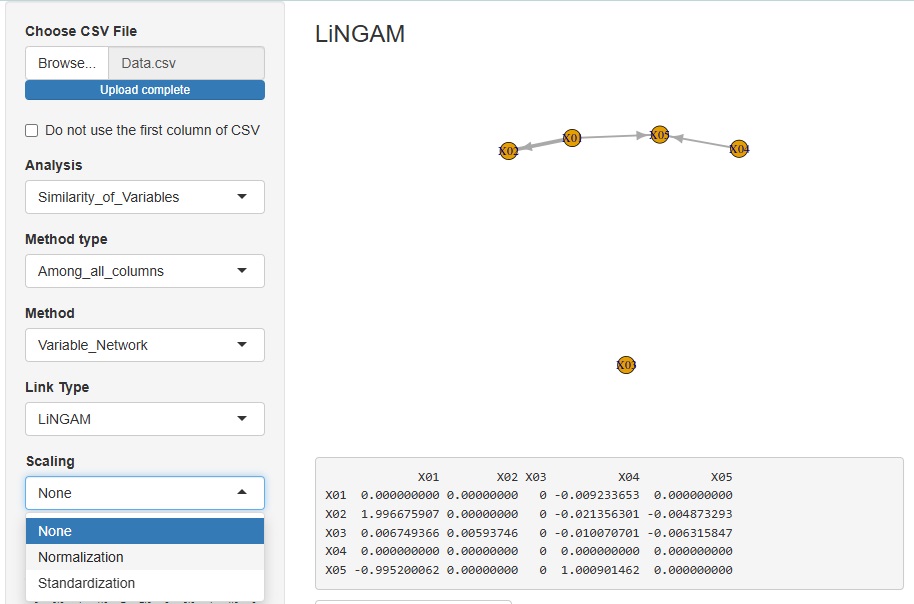
R-EDA1 では、標準化や正規化をして変数の関係をみる分析が、簡単に試せます。
順路


 次は
主成分分析
次は
主成分分析

