
LiNGAM is a method for finding the coefficients of a structural model, so it requires some ingenuity when used for Analyzing variable companioning.
Standardization and Normalization are the ingenuity.
This device can be used as a device to analyze data that is the Limit of LiNGAM without making a mistake.
Among the stories that are at the limit of LiNGAM , "when one error is extremely large", "when one error is extremely small", and "when the coefficient is extremely small" can be standardized or normalized. , The relative size relationship does not change, so it has no effect.
For "when the coefficient is extremely small and the error on one side is extremely small", standardization or normalization will change the result. The problem with "when the coefficient is extremely small and the error on one side is extremely small" is that the part that you want to be 0 is no longer 0, and the part that you do not want to be 0 becomes 0.

However, for example, if you standardize each variable before LiNGAM, the result will be as follows. You can't get the number "0.01", but at least you can make sure that the structure of the formula is correct.
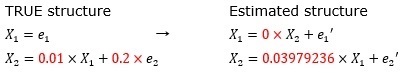
Suddenly, suppose that the following formula is obtained as a result of LiNGAM.
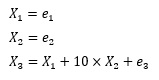
Looking at the magnitude of the coefficient, X1 is 1 and X2 is 10 for X3. However, it is a mistake to conclude from this information that "X2 has a stronger relationship with X3 (more correlation)".
If you have X3 on the vertical axis and X1 and X2 on the horizontal axis, you may get the above results in LiNGAM, even in the graph below. Looking at this graph, it is X1 that has a stronger relationship with X3.
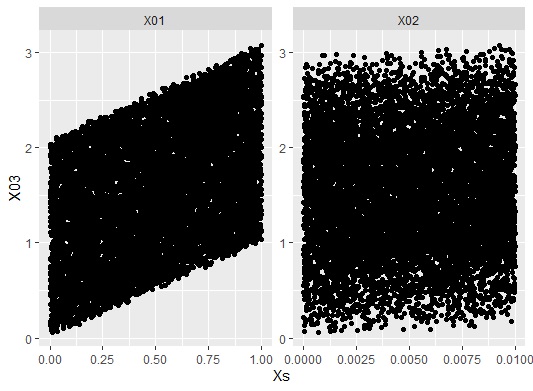
This phenomenon occurs when the magnitudes of the variations of e1, e2, and e3 are extremely different.
When performing Multi-Regression Analysis , if you want to see the degree of influence on the objective variable Y for variables with different units, you have to look at the standard partial regression coefficient instead of simply the coefficient of each variable when performing multiple regression analysis. , Will be a mistake. This is because the units of the coefficients are different, and the numbers with different units are compared.
The standard partial regression coefficient is a coefficient that can be obtained by standardizing each variable and then performing multiple regression analysis, but if you use this, the units will be the same, so the above error will be eliminated.
The same thing happens when using LiNGAM to look at the strength of variable relationships. Therefore, it is necessary to perform standardization and normalization as preprocessing of variables .
After standardization and normalization , the coefficient number can be used as a number to indicate the degree of influence of the variable.
In the case of the above example, if you standardize and then perform LiNGAM, the result below will be obtained. The coefficient of X1 is 10 times larger than the coefficient of X2, and the strength of the relationship can be seen by the magnitude of the coefficient.
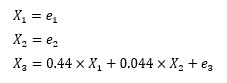
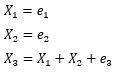
Suppose there is a variable with the structural formula.
In this case, when the error terms of e1, e2, and e3 all vary within the same range, LiNGAM can correctly estimate the structural formula, so the relationship between variables can be analyzed correctly.
However, if only e3 is extremely small, the following three equations will be similar to the same thing, and it will not be possible to specify the structure with LiNGAM.
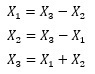
Standardization and normalization do not solve this problem .
However, if we can assume that "variable relationships should only hold for addition", we may be able to solve it by adding the condition "negative signs are not allowed" to the algorithm.
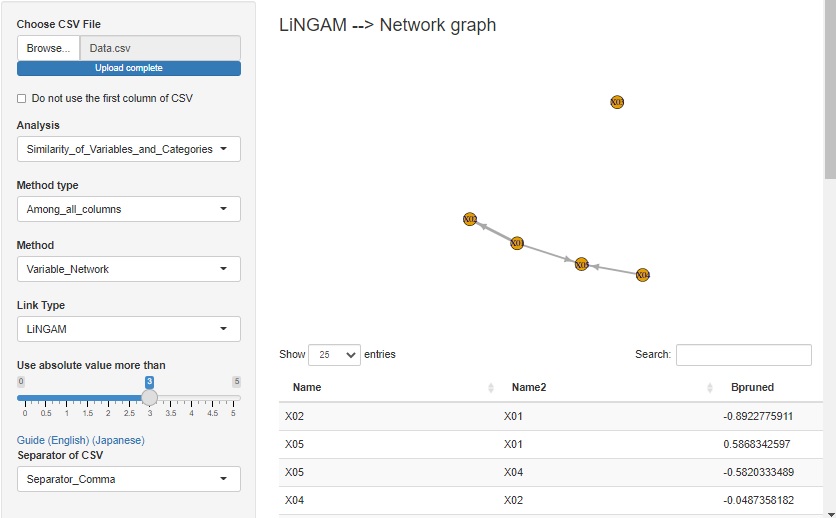
With the software below, you can try analysis to see the relationship between variables by standardizing.
An example of LiNGAM by R
By
R-EDA1,
you can easily try LiNGAM.
NEXT 

 Principal Component Analysis
Principal Component Analysis
