R-EDA1�ɂ��f�[�^�����@�b�@R�ɂ��f�[�^����
R-EDA1�ɂ��f�[�^�����@�b�@R�ɂ��f�[�^����
 R-EDA1�ɂ��f�[�^�����@�b�@R�ɂ��f�[�^����
R-EDA1�ɂ��f�[�^�����@�b�@R�ɂ��f�[�^����
R-EDA1 �̃����[�X�m�[�g�ł��B GitHub�� https://github.com/ecodata22/R-EDA1 �Ńo�[�W�����Ǘ����Ă���̂ŁA������ɂ��X�V�̃R�����g�͓���Ă��܂����A�p��ł����A �R�[�h�̂ǂ����ς�����̂������A�ł��邱�Ƃ̉����ς�����̂��ɋ�����������̕��������Ǝv���܂��̂ŁA���̃y�[�W������Ă��܂��B
���Ȃ݂ɁA���̃T�C�g�̍X�V�́A �g�b�v�y�[�W �� �Â��X�V���� �ɂ���܂��B
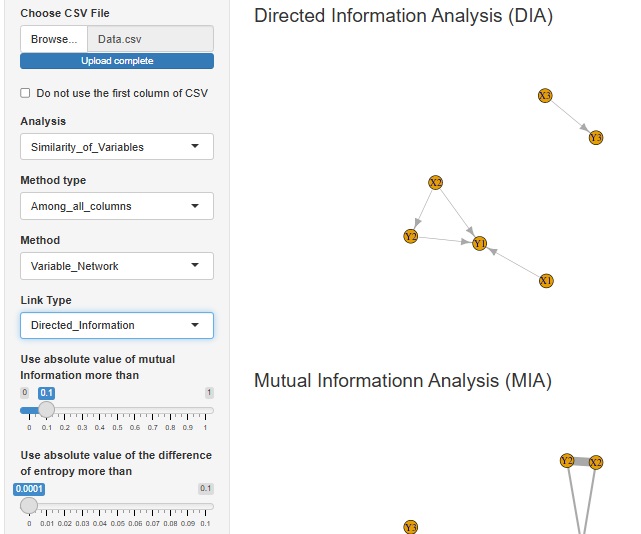
�L�����ʕ��� �iDirected Information Analysis : DIA�j �̋@�\��lj����܂����B
�܂��A�ʓI�ϐ�������A���I�ϐ��ɕϊ����܂��B
���ɁA���ݏ��ʂ��v�Z���āA���ݏ����̍����ϐ��̑g�����𒊏o���܂��B�iMutual Informationn Analysis : MIA�j
�Ō�ɁA���ݏ��ʂ̍����ϐ��̑g�����ɂ��ẮA���Ϗ������ׂāA���̕��������߂܂��B
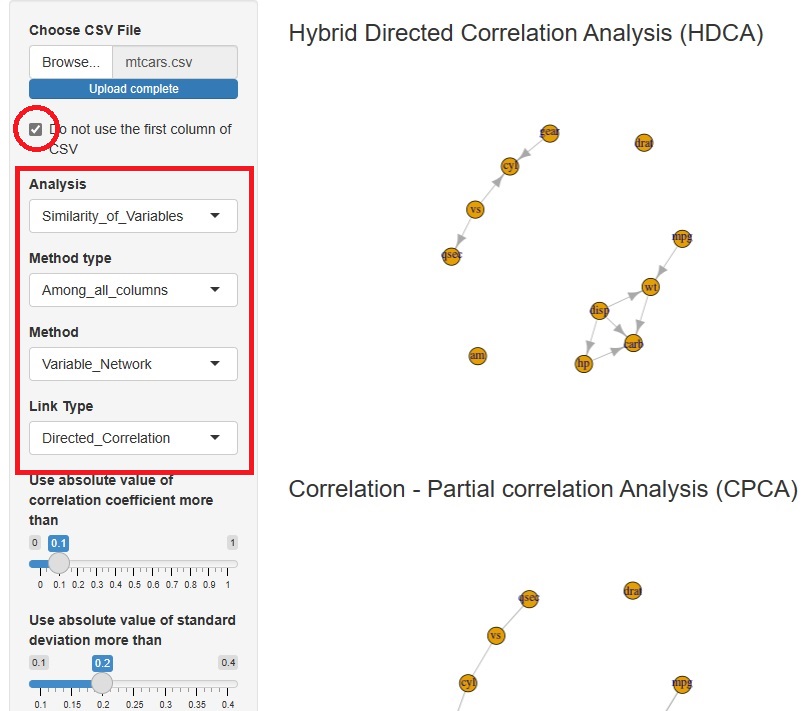
�n�C�u���b�h�L�����֕��� �iHybrid Directed Correlation Analysis : HDCA�j �̋@�\��lj����܂����B
�܂��A���W���ƕΑ��W���ŁA���̌�������������G�b�W����肵�܂��B ���ɁA�����t���Ɨ������Ŕ��f�ł�������𒊏o���܂��B �Ō�ɁA�����t���Ɨ��ł͔��f�ł��Ȃ������ɂ��āA���K���ƕW�������g���Č����f���܂��B
�����t���Ɨ����ł��邾���g�����ƂŁA LiNGAM�ł͈����Ȃ��f�[�^�ł��A�ł��邾���Ή����܂��B
�܂��A���K���ƕW���ϐ����g�����ƂŁA�����t���Ɨ��i
�x�C�W�A���l�b�g���[�N
�j�����ł͌��܂�Ȃ��p�^�[���ɑΉ����܂��B
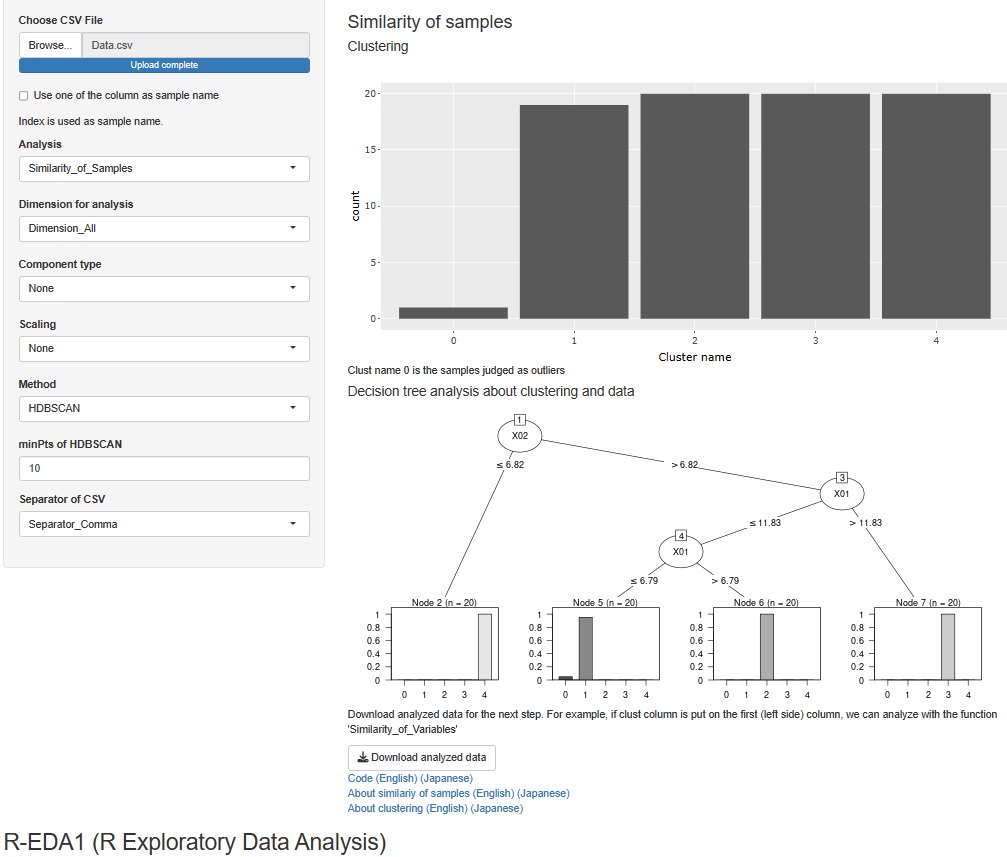
�S�ϐ��ɂ��ẴN���X�^�[���͂́A�K�w�^�ADBSCAN�AHDBSCAN������܂������A����ɍ������z�@��lj����܂����B
�܂��A�S�ϐ��ɂ��ẴN���X�^�[���͂������ꍇ�A���܂ł́A���̃f�[�^�ɃN���X�^�����O�̌��ʂ�lj������f�[�^���Acsv�t�@�C���ŏo�͂ł���悤�ɂȂ��Ă��������ł������A�N���X�^�[��ړI�ϐ��Ƃ�������ؕ��͂��ł���悤�ɂ��܂����B
�N���X�^�����O�̌�������
���ł��܂��B
���I�ϐ����_�~�[�ϊ�����ƁA�ʓI�ϐ��̗ގ��x�̕��͂̕��@���A�J�e�S���̗ގ��x�̕��͂̕��@�Ƃ��Ďg�����Ƃ��ł��܂��B ���̂��߁A�ϐ��ƃJ�e�S���̕��͂́A�����Ƃ���ɂ���Ă��܂����B
�܂��A�J�e�S���̗ގ��x�̕��͂́A�A�\�V�G�[�V�������͂����Ȃ��Ǝv���Ă������Ƃ�����A�J�e�S���̗ގ��x�̕��͂����ŁA�ЂƂ̒��ɂ͂��Ă��܂���ł����B
�������A���I�ϐ����_�~�[�ϊ����āA�ϐ��̗ގ��x�̕��͂��g�����A�ʓI�ϐ������I�ϐ��ɕϊ����āA ���I�ϐ��̗ގ��x�̕��͂�������A�J�e�S���̗ގ��x�̕��͂Ɏ������ޕ����A�ǂ����Ƃ������ł��B �܂��A�R���X�|���f���X���͂́A�J�e�S���̗ގ��x�̕��͂ł��B
�����ŁA���������܂����B
�听����A���� �� �ʂ̈��q�̊�^�� �̕��͂�lj����܂����B �S��ނ̊�^�����g�������͂��ł���悤�ɂȂ�܂����B
�_�~�[�ϊ� �́A�udummies�v�ƁufastDummies�v�̂Q���g�������Ă����̂ł����A�S���A�ufastDummies�v�ɓ��ꂵ�܂����B
�udummies�v��CRAN����폜����Ă��܂��A�g���Ȃ��Ȃ����̂����R�ł��B
������̃��C�u�������A�ʓI�ϐ��Ǝ��I�ϐ����������Ă��鎞�ɁA���I�ϐ�������ϊ����Ă����Ƃ��낪�֗��ł��B
�����A�ufastDummies�v�ɂ́A�u�S�����ʓI�ϐ��ŁA�ϊ��Ώۂ��ЂƂ��Ȃ��ƃG���[�ɂȂ�v�Ƃ�����_������܂��B �����ŁA�ϊ��̑O�ɁA�S���̕ϐ����`�F�b�N���āA�ϊ��Ώۂ��Ȃ���A���̃��C�u�����͎g��Ȃ��悤�ɂ��܂����B ���̂��߁A�]���A�P�s�ōς�ł����Ƃ��낪�A�T�s�ɑ����Ă��܂��B
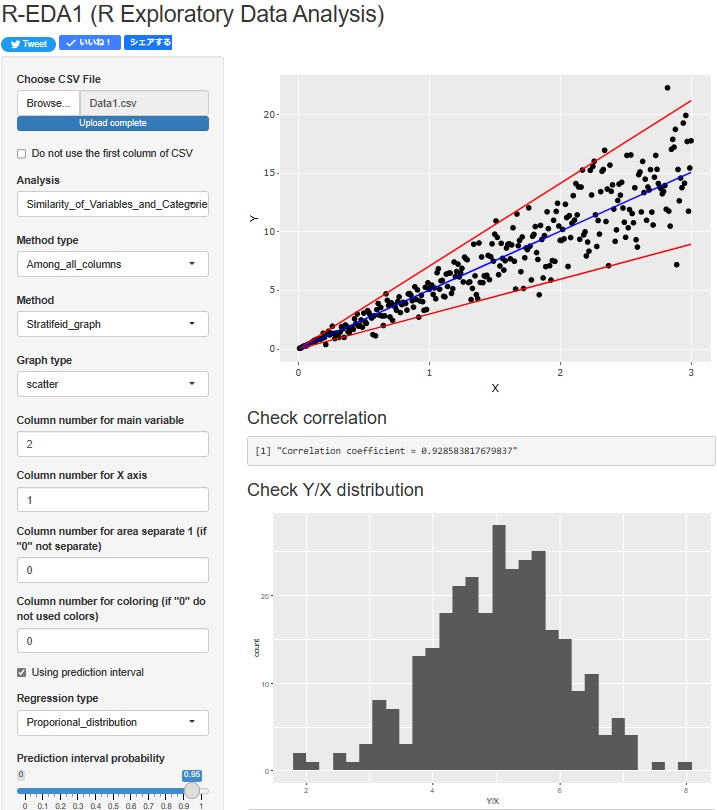
��ᕪ�U�̉�A���� ���ł���悤�ɂ��܂����B �㑤�̎U�z�}�ɂ́A ��ᕪ�U�̗\����� ���o�܂��B �܂��A�����̃q�X�g�O�����́A��ᕪ�U�̌��ɂȂ��Ă���uY/X�v�̕��z���킩��悤�ɂ��Ă���܂��B
�������֕��͂ō��������Q�����Ɉ��k �̕��͂̋@�\��lj����܂����B
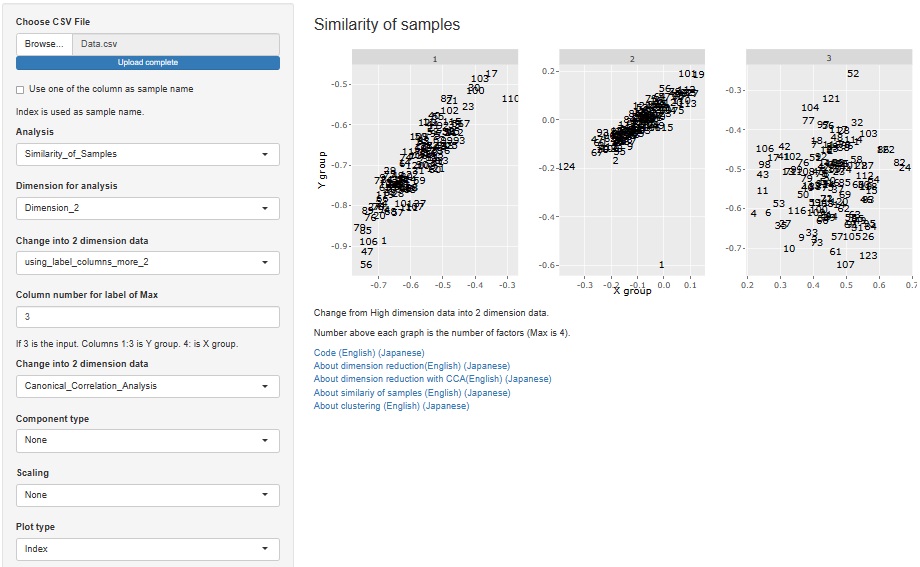
R�ɂ�鐳�����֕���
�ɂ́A�J�[�l���@�ɂ�����`�̐������֕��͂�����܂����A������g����悤�ɂȂ��Ă��܂��B
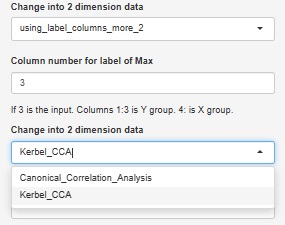
��A���͌n�ō��������Q�����Ɉ��k���ĉ��� �� �c���̊O��l �̕��͂̋@�\��lj����܂����B
��A���͌n�̕��@�Ƃ��ẮA ��A���� �A ���f���� �A �T�|�[�g�x�N�^�[��A �̂R��ނ��g����悤�ɂȂ��Ă��܂��B
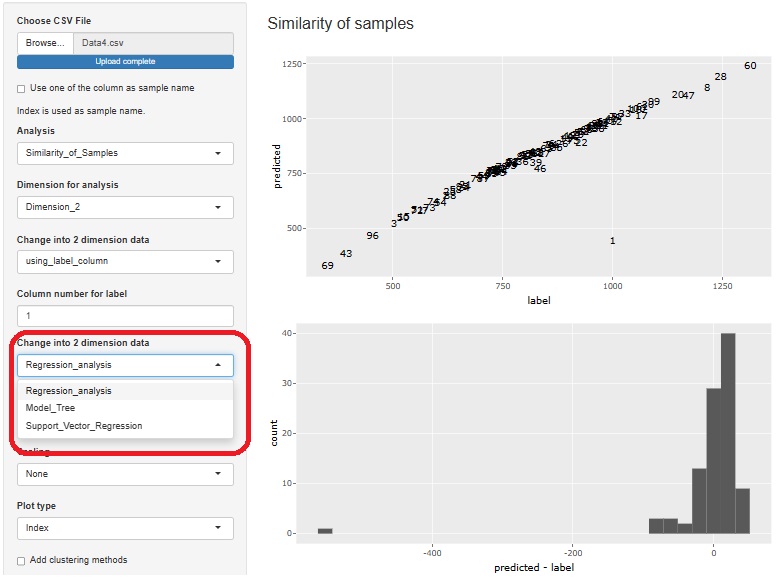
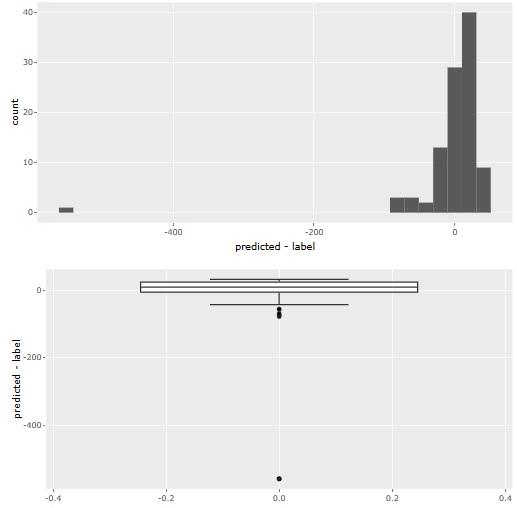
�c���̕��͂́A�q�X�g�O�����Ɣ��Ђ��}�̗������o�܂��B
�q�X�g�O�������ƁA�T���v���������ɑ傫���Ȃ������ɁA�O��l�������ɂ����Ȃ�̂ŁA���������ꍇ�͔��Ђ��}�̕����ǂ��ł��B
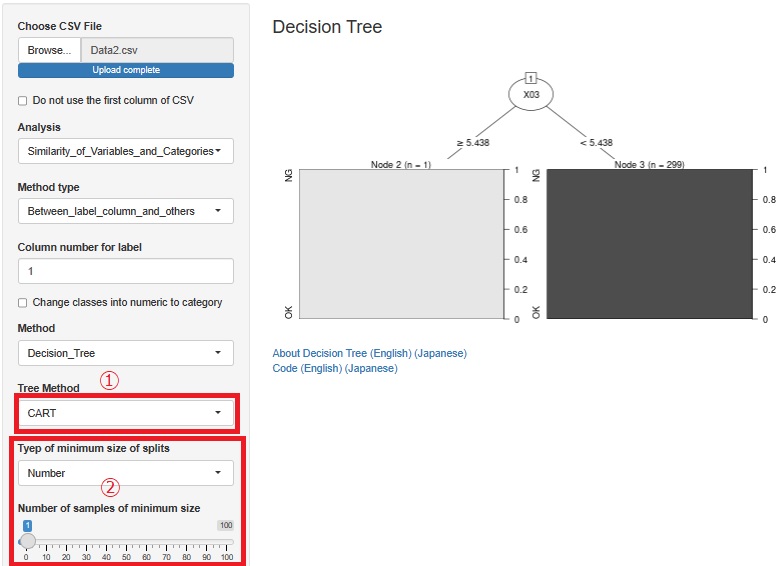
����� ��CART��lj����܂����B�}�̇@�̂Ƃ���ł��B C5.0������̂ŁACART�͕s�v�Ǝv���Ă����̂ł����AC5.0�͕���̃��[���������߂̂悤�Ȃ̂ŁACART������邱�Ƃɂ��܂����B
�܂��A R�ɂ��X�̃T���v���̈��ʐ��_ �̃y�[�W�̎g�������ł���悤�ɁA�ŏ��T���v�����������ł���悤�ɂ��܂����B ���܂ł́A�ŏ��T���v�����̊����iRatio�j�����������ł���悤�ɂ��Ă����̂ł����A��̓I�ȃT���v�����̎w����ł���悤�ɂȂ�܂����B�}�̇A�̂Ƃ���ł��B
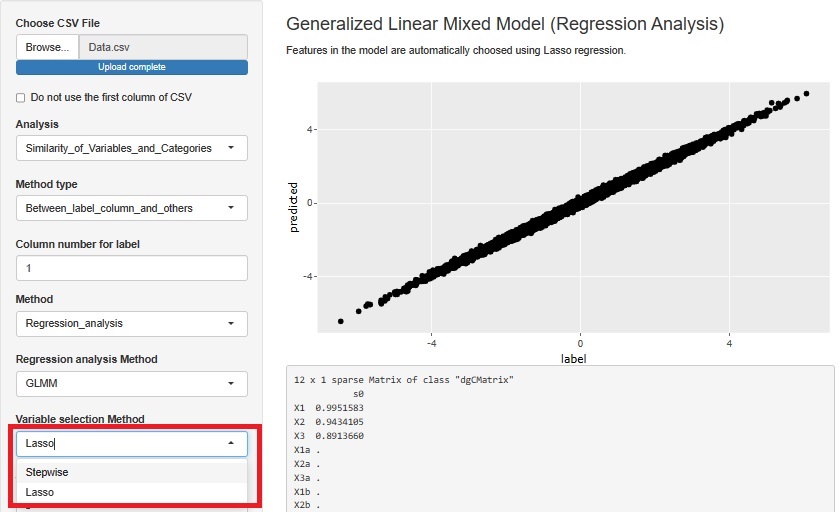
R�ɂ��ϐ��̏d�v�x�̕��� �ɂ��� ���b�\��A ��lj����܂����B
�u ���b�\��A �̋@�\��lj��v�Ƃ��������A ��ʉ����`���f�� �̕ϐ��̑I���̕��@���A���܂ł̃X�e�b�v���C�Y�@�ɉ����āA���b�\��A���������A�ʒu�t���ɂ��Ă��܂��B
�o�͂Ƃ��ďo�ė���U�z�}�́A�\���l�Ǝ����l�̊W��������悤�ɂ��Ă��܂��B ������Ȃ�A���x���������ƂɂȂ�܂��B ���̖@�ɂ���ϐ��Ɛ��l�̃��X�g�́A�W���Ή�A�W���̌v�Z���ʂɂȂ��Ă��܂��B ����ɂ���āA�ϐ��̏d�v�x���]���ł��܂��B
R�ɂ��x�C�W�A���l�b�g���[�N �ɂ�����܂����A�x�C�W�A���l�b�g���[�N�̂������̃A���S���Y���́A�����g���ĕϐ��̊W�̗L���肵�܂��B
���܂ł́A�f�t�H���g�l�i0.05�j�����g���Ȃ������̂ł����A�ύX�ł���悤�ɂ��܂����B
�T���v�������������́A��������������������A�Ӗ��̂�����������₷���Ȃ�܂��B
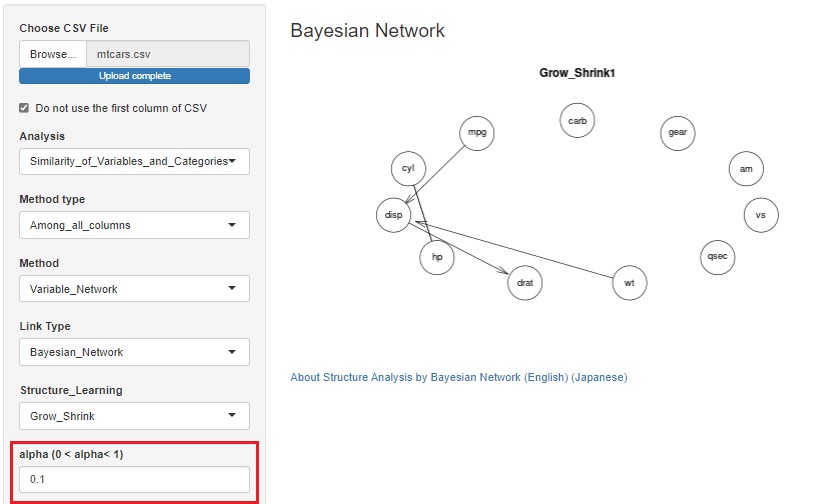
���f���� ��lj����܂����B ��ʓI�ȉ�A�́A�O���[�v���͗\���l�����̂��߁A�\���l�̐��x���グ�悤�Ƃ���ƕ��G�߂��čl�@���ł��Ȃ����f���ɂȂ��_������܂����B ���f���́A�O���[�v���͉�A�����g�����߁A�V���v���ȃ��f�������₷���Ȃ�܂��B
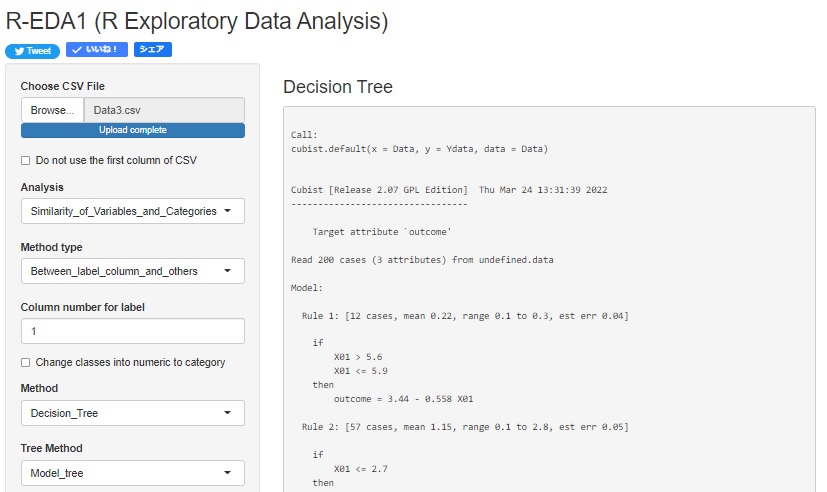
�ϐ��̑��֊W���l�b�g���[�N�O���t�Ō�����@�̂ЂƂ� LiNGAM ��lj����܂����B
�덷�����K���z�ȊO�ŁA�ϐ��� �p�X��� �̎��̍\���������Ă��鎞�ɁA���̍\�������Ԃ�o�����Ƃ��ł��܂��B
�Ȃ��ALiNGAM���g����R�̃��C�u������pcalg������܂����Apcalg�́Ashiny�̃T�[�o�ł̓G���[���o�Ďg���Ȃ����߁A �M�҂����삵���R�[�h���g���Ă��܂��B �R�[�h�́A R�ɂ��LiNGAM �ɂ���܂��B
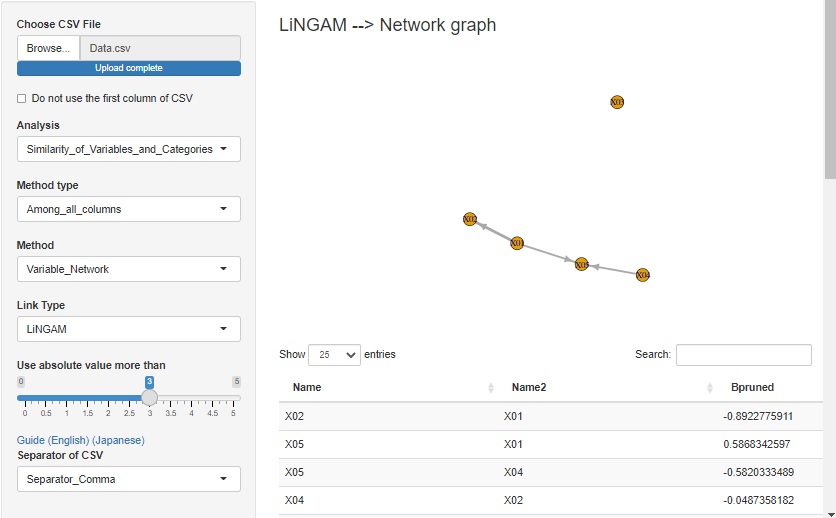
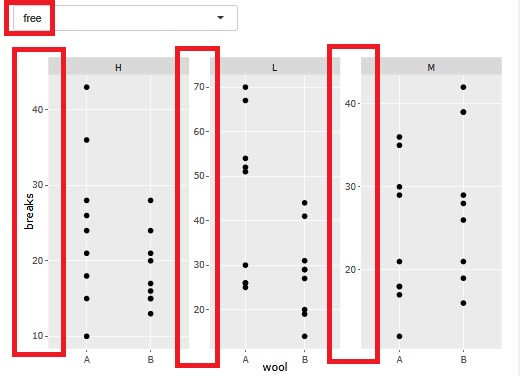
�w�ʂ̕��͂����鎞�ɁA�O���t��w�ʂŕ����ł���@�\������܂��B ���̃O���t�̎��ɁA���܂ł́A�O���t���Ƀv���b�g�����n����悤�Ɏ��͈̔͂�����Ă��܂����B
�f�[�^�}�C�j���O �̂悤�ȕ��͂̎��ɂ́A�����ȗ̈�ŋN���Ă��邱�Ƃ��g�債�Č���ړI�ł͗ǂ������̂ł����A �S�̓I�Ȉʒu�t�������������ɂ́A�킩��ɂ����Ȃ��Ă��܂����B
�����ŁA���͈̔͂����킹�邩�ǂ����́A�I�ׂ�悤�ɂ��܂����B
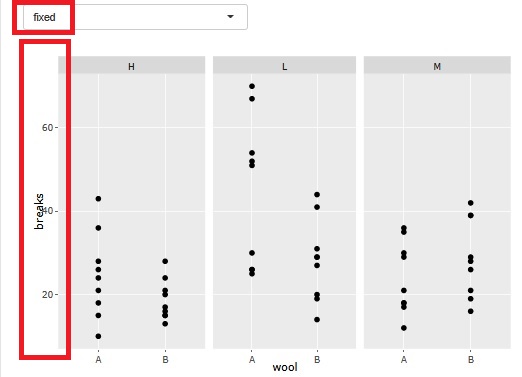
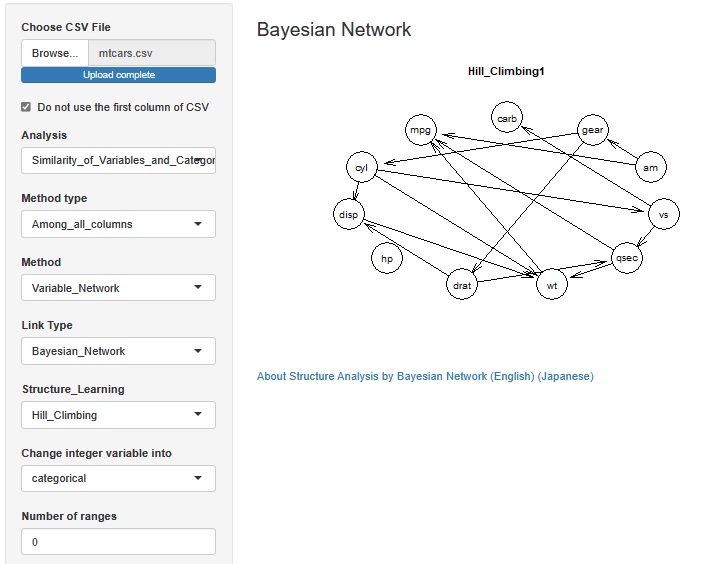
�x�C�W�A���l�b�g���[�N�ɂ��f�[�^�̍\����� �ł́A�����̕ϐ��́A���I�ϐ��Ƃ��Ĉ������A�ʓI�ϐ��Ƃ��Ĉ����̂���I�ׂ�悤�ɂ��܂����B
��ʓI�ȗʓI�ϐ��ł́A���I�ϐ��Ƃ��Ĉ������ɁA��Ԃŋ����@���g���܂����A ���̋@�\�Ő��������I�ϐ��Ƃ��Ĉ������́A�Ⴆ�A�u�P�A�Q�A�T�v�Ƃ����R�̐���������A�����̂R�����ꂼ�ꎿ�I�ϐ��Ƃ��Ĉ����܂��B
�����ŕ\����Ă���ϐ��������n�̕ϐ��̎��́A�x�C�W�A���l�b�g���[�N�ł́A���̌��̕��Ɏ��I�ϐ���u���̂ŁA
�v�����悤�Ȗ��ɂȂ�₷���Ȃ�܂��B
�L�������� �̕��͂����ł����A�����s����X�^�[�g�ɂ��镪�͕��@������܂��B
���̕��@�́AR-EDA1�ł� �������ړx�\���@ �������g����悤�ɂ��Ă����̂ł����At-SNE�AUMAP�A�K�w�^�N���X�^�[���͂ł��ł���悤�ɂ��܂����B
t-SNE
t-SNE�̏ꍇ�́A�������͂R���ő�l�ł��B
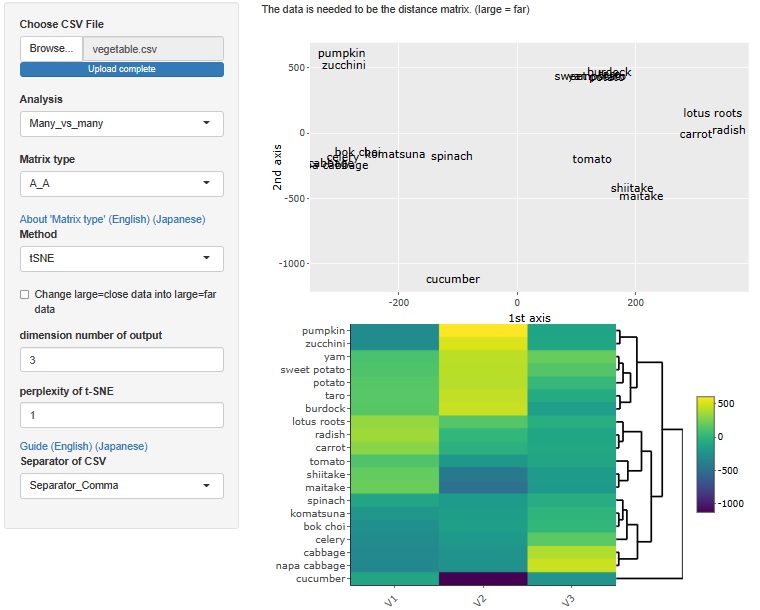
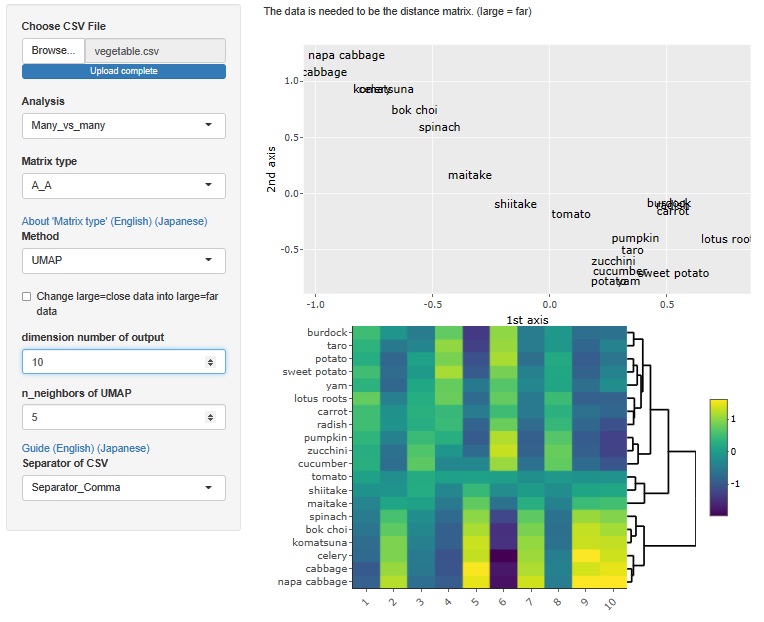
UMAP
UMAP�̏ꍇ�́A�������̓T���v���̐����ő�l�ł��B
�����A�\�t�g�Ƃ��ẮA�傫�Ȏ������ł����͂ł���悤�ɂ��Ă��܂����A���̌��ʂ̕����I�ȍl�@�̎d�����������ړx�\���@�̎��̂悤�ɂ͂ł����A
�M�҂Ƃ��Ă͎g�������킩��Ȃ��ł��B
�K�w�^�N���X�^�[����
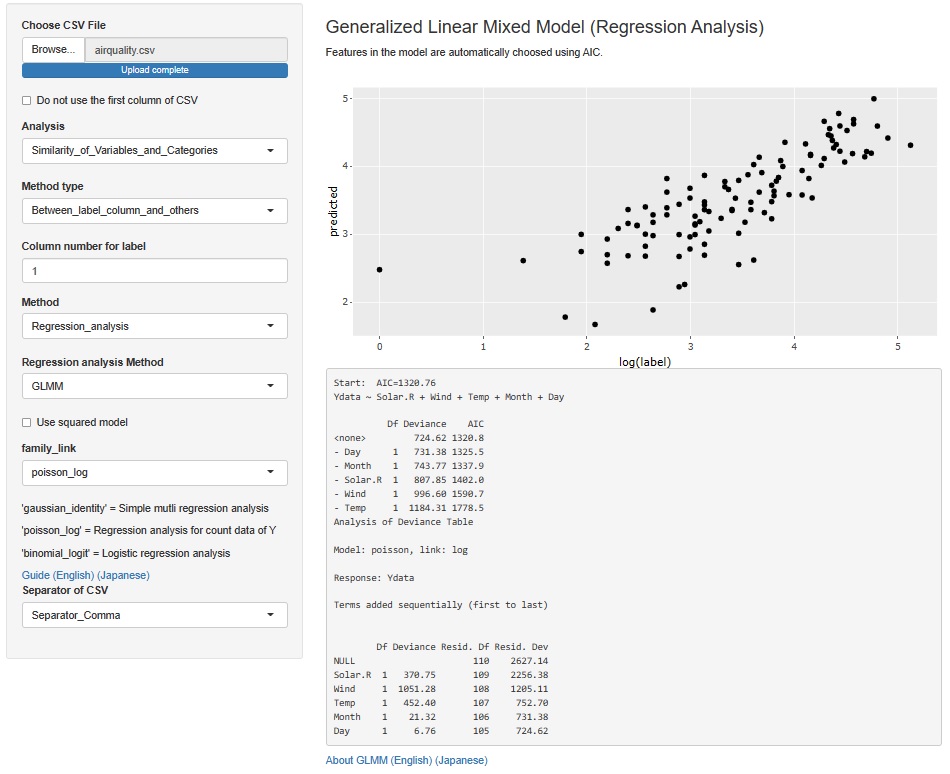
��ʉ����`�������f�� �̌��ʂ́A�e�L�X�g�����������̂ł����A���x���̗\���l��Y���A�����l��X���ɂ����O���t���o�͂���悤�ɂ��܂����B R2��AIC�Ȃǂ̎w�W�Ō�������A���f���̏o���h�����킩��₷���ł��B
��ʉ����`�������f���iGLMM�j�́A�Q�̏ꏊ�ɓ����Ă��܂����A�����ɂ��̋@�\��lj����Ă��܂��B
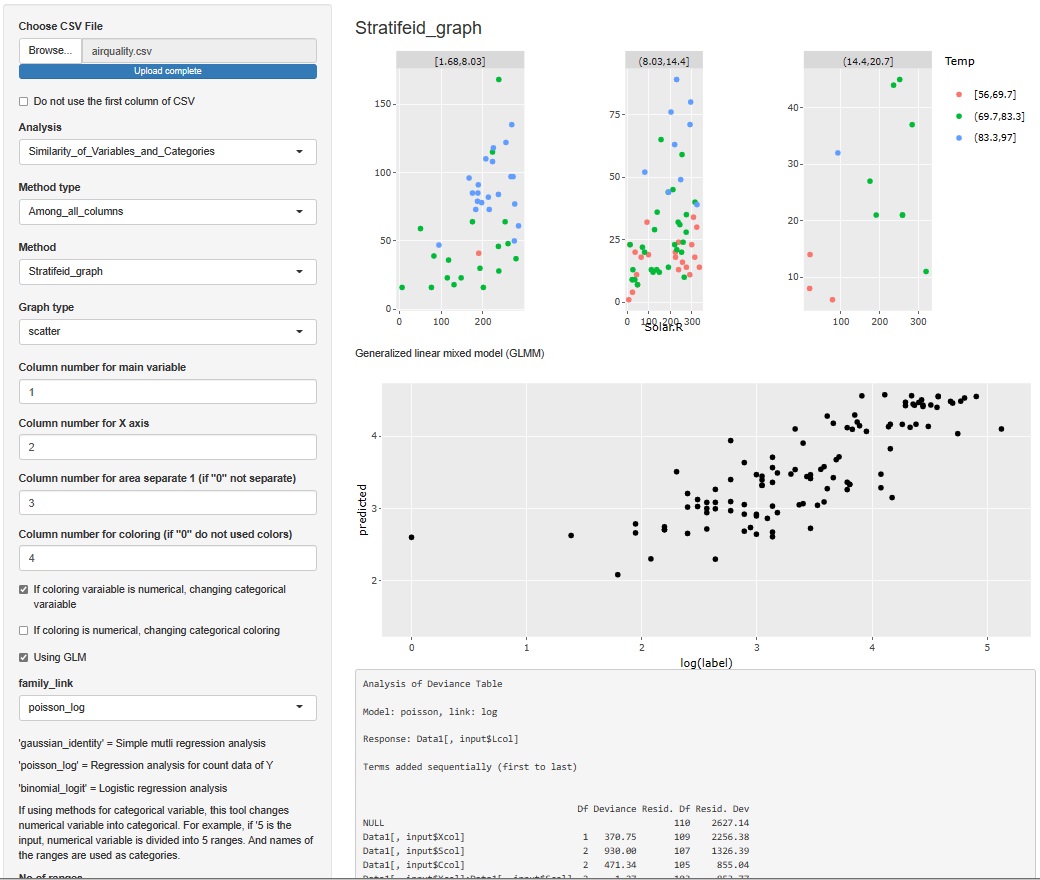
�O���t�ɂ�����A�v�Z������Ƃ킩��Ȃ��Ȃ�̂ł����A �f�[�^���͂����鎞�́A���f�[�^�i���͑Ώۂ̃f�[�^�j�̋�̓I�Ȓl���ǂ��Ȃ��Ă���̂����m�F����ƁA �ǂ����Ƃ�����܂��B �����̗��_���g��Ȃ��Ă��A�f�[�^�����������Łu����͕ς��v�Ƃ킩�邱�Ƃ�����܂��B
�S������@�\��t����̂͑�ςȂ̂ŁA�����������āA��ԏ�iHead�j�ƈ�ԉ�(Tail�j�̂T�s�����m�F�ł���悤�ɂ��܂����B
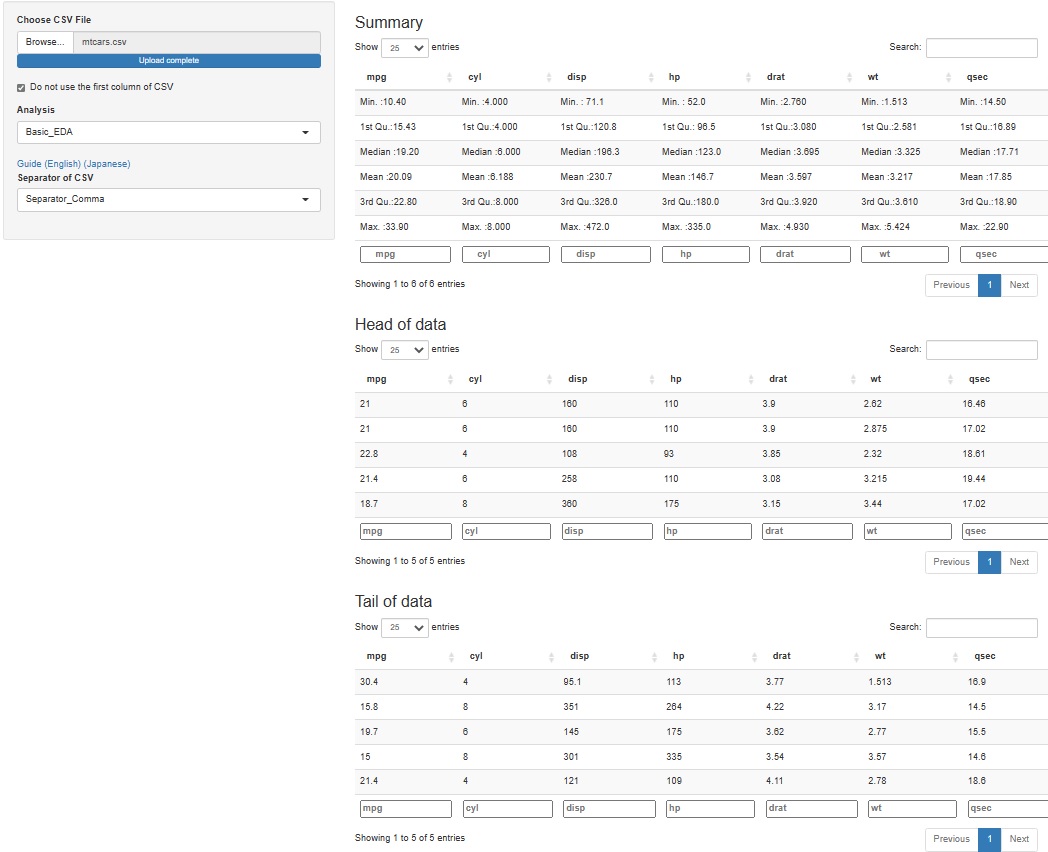
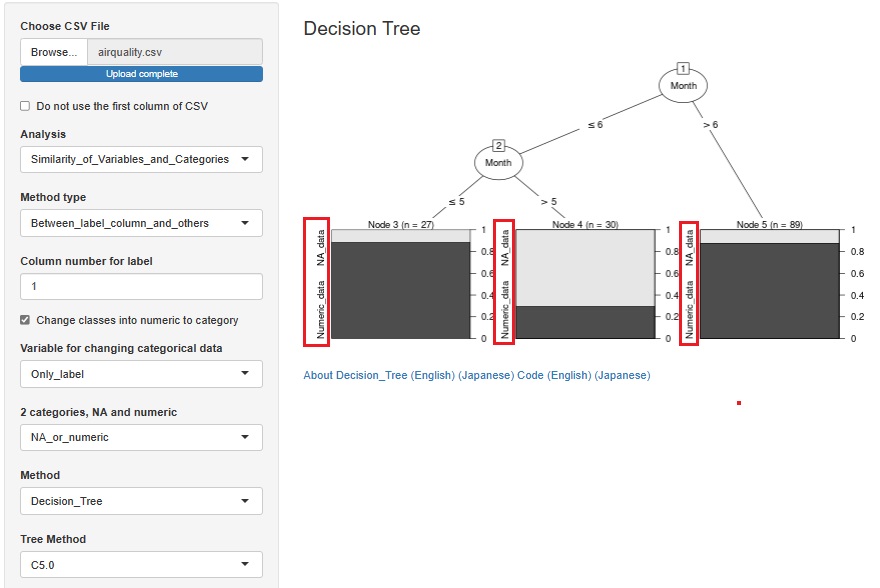
�����l���܂ޗʓI�ϐ���ړI�ϐ��ɑI���ɁA �����l���uNA_data�v�A�����l�ȊO���uNumeric_data�v�Ƃ������O�̎��I�ϐ��ɕϊ�����@�\��lj����܂����B
�����l���������Ă��闝�R���A���̕ϐ��Ƃ̊W���璲�ׂ��܂��B �܂��A���̕ϐ��Ɖ����W���Ȃ������ȏꍇ�́A�u�����̓����_���ɔ������Ă���v�Ƃ����l�@���ł��܂��B
�܂��A�����ɖړI�ϐ��ɂ��āA�c�������ׂĂ̑��̕ϐ��ɂ��āA�w�ʂ̂P�����U�z�}������ł��B
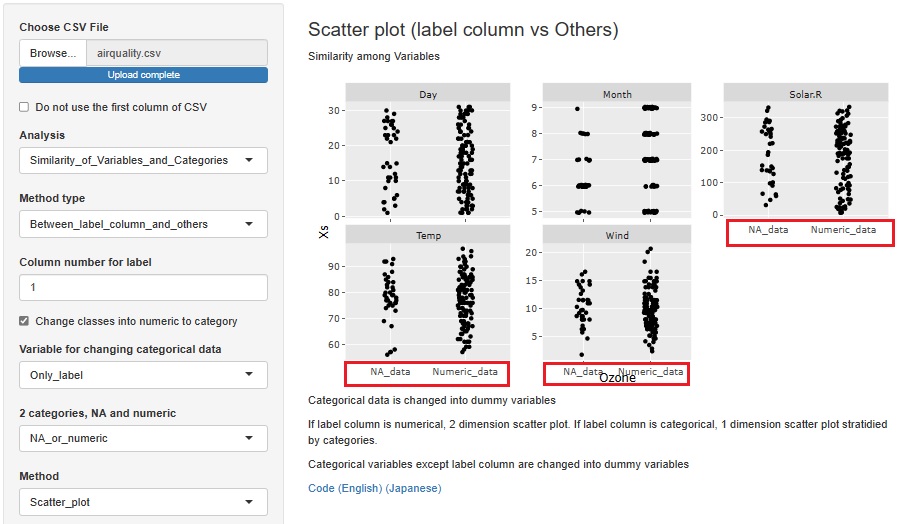
������̗�ł��B
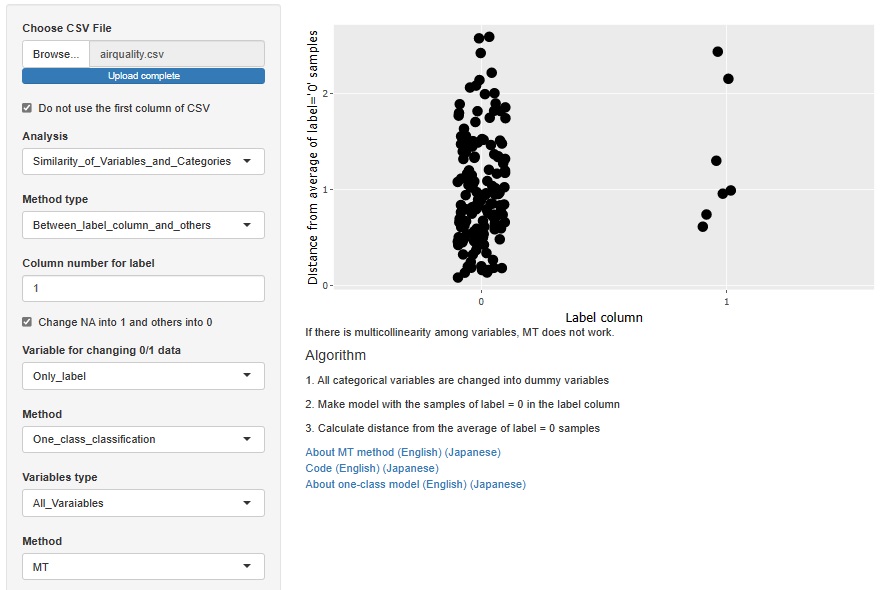
MT�@�̗�ł��B
MT�@�̏ꍇ�́A�P�ʋ�Ԃ��������Ă��Ȃ��T���v���ɂ��Ă��܂��B
�u0�v�������l�ł͂Ȃ��T���v���ŁA�u1�v�������l�̃T���v���ł��B
�������Ă��闝�R�����낢�날��ꍇ�́A�������MT�@�̕����ǂ��ł��B
�听���ɕW������K�� �̋Z���R�̎�@�Ŏg����悤�ɂ��܂����B
���������Q�����Ɉ��k���ĉ���
�̕��@���g�����ɁA��L�̕��@��P�Ƃ�A�g�����Ďg����悤�ɂ��Ă���܂��B
�g�ݍ��킹���ꍇ�́A�听�����͂���ɏ�������܂��B
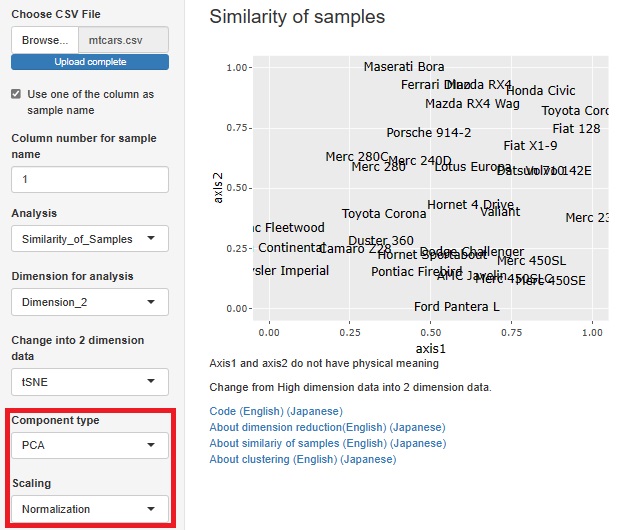
1�N���X�ŏ������@
�ł��A�g�������܂��B
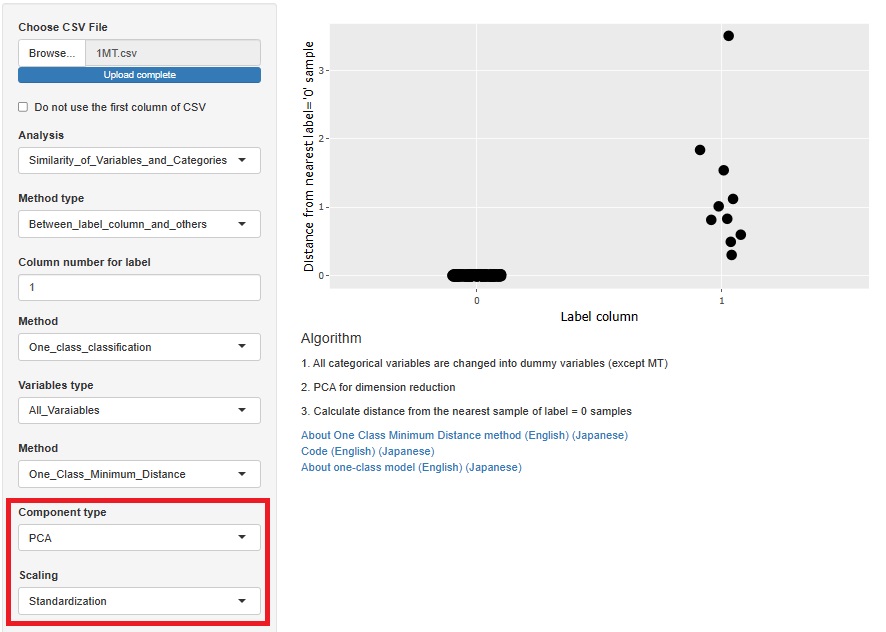
���n����
�ł��A�g�������܂��B
���n����
�ł́A�听�����́iPCA�j�����łȂ��A
�Ɨ����������iICA�j��
���q�����iFactor_analysis�j�Ƃ��g�������܂��B
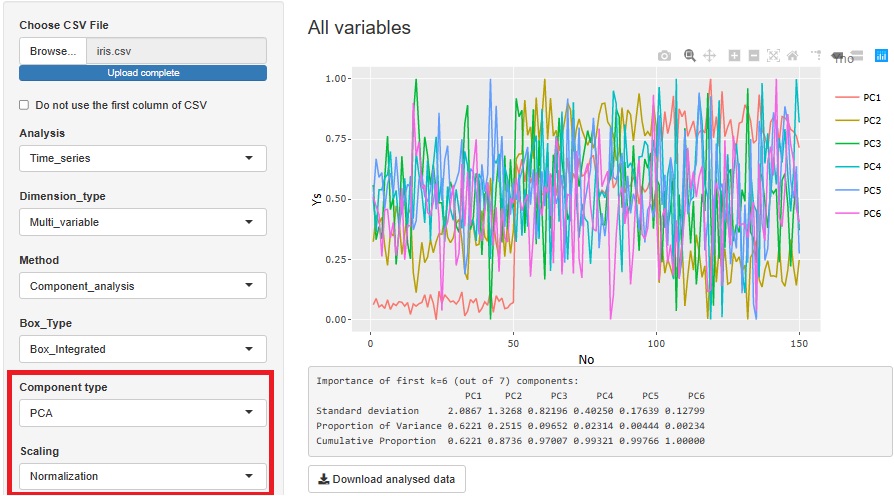
���q���͂��A�T���v���̗ގ��x�̕��͂���A���Α��̕��͂Ɉ��z���܂����B
�T���v���̗ގ��x�̕��͂̕��@�́A��{�I�ɕϐ��ƃT���v���̊W�͌��Ȃ��̂ł����A���̓_���A�����ɔz�u�������̕��@�ƍ���Ȃ��̂ŁA
���K�ȏꏊ�Ɉړ����܂����B
HDBSCAN��lj����܂����B DBSCAN�Ǝ��Ă��܂����A���x�̍�������N���X�^�����鎞�ɁA���܂������Ă����悤�ɂȂ��Ă��܂��B
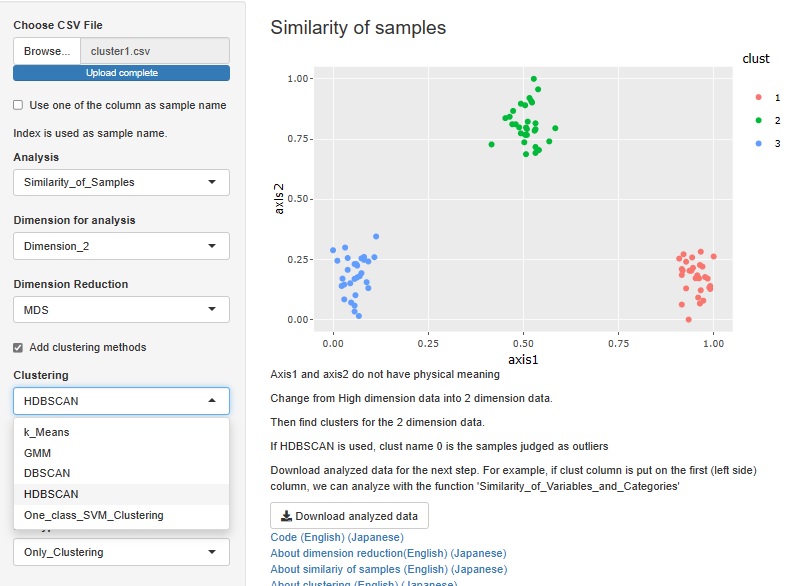
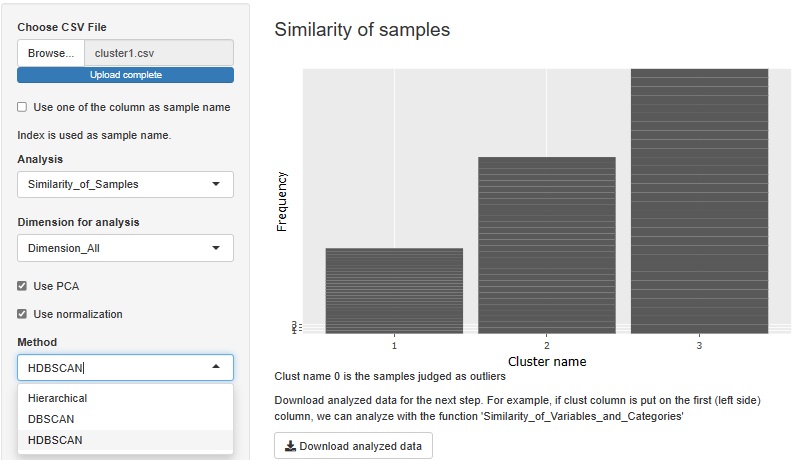
MDS�i�������ړx�\���@�j��t-SNE���I�ׂ�悤�ɂȂ��Ă��鏊�ɁA�uUMAP�v���I�ׂ�悤�ɂ��܂����B
 �@
�@
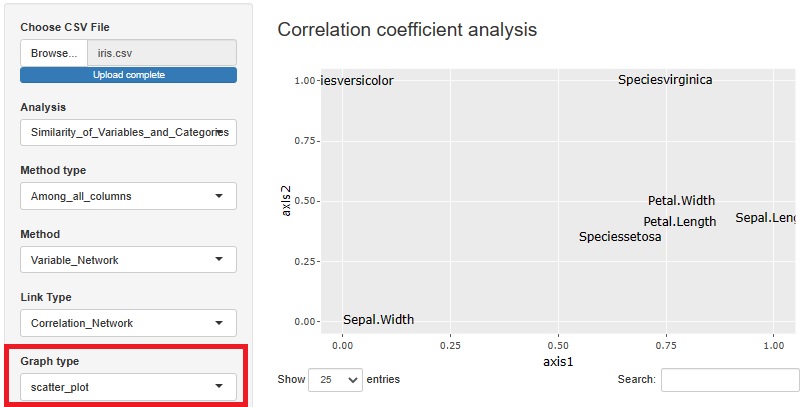
���W���A�O���t�B�J�����X�[�A�N�����[���̘A�W�����l�b�g���[�N�O���t�Ō�����@�����Ă��܂������A �O���t�͎U�z�}�ɂ��Ȃ�悤�ɂ��܂����B
�����̓l�b�g���[�N�O���t�Ǝ��Ă��āA�ʒu���߂��ϐ����m�͌W���������ł��B
�l�b�g���[�N�O���t���ƁuA��B�͋߂��BA��C�͋߂��BB��C�͂����������v�Ƃ����ꍇ�ɁA�����N�̗L���ŊȒP�ɕ\���ł���̂ł����A �U�z�}���ƁA�uB��C�͂����������v�Ƃ������Ƃ��\���܂���B ����������_�͂���̂ł����A�U�z�}�̓O���t���y���̂ŁA���̓_�̓l�b�g���[�N�O���t�����ǂ��ł��B
 �@
�@
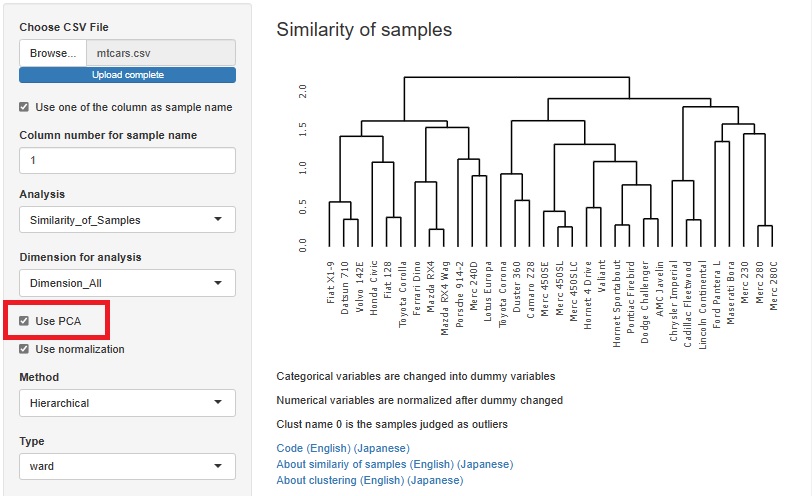
�N���X�^�[���͂����鎞�ɁA�O�����Ƃ��Đ��K����I�ׂ�悤�ɂ��Ă����̂ł����A ���K���̑O�Ɏ听�����́iPCA�j�����āA�听����ϐ��Ƃ��Ďg����悤�ɂ����܂����B ���K��������E���Ȃ��ƁA�听�����͂�����E���Ȃ��A�łS�ʂ�̑g�������ł��܂��B �ǂ������������f�[�^�ŁA�ǂ��������Ɍ������̂��őI�ׂ�悤�ɂȂ��Ă��܂��B
 �@
�@
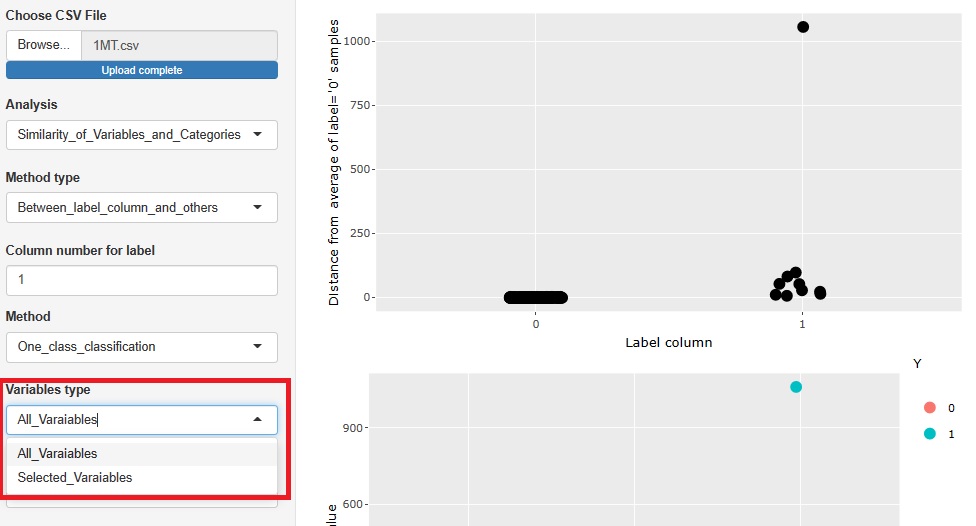
�P�N���X�̎�@�́A�ϐ��S���Ń��f��������ĕ��͂�����̂ƁA�P�`�R�̕ϐ��̑S���̑g�����Ń��f��������āA�g�����̈Ⴂ�͂�����̂�����A�ꏏ�ɂȂ��Ă����̂ł����A�������܂����A
 �@
�@
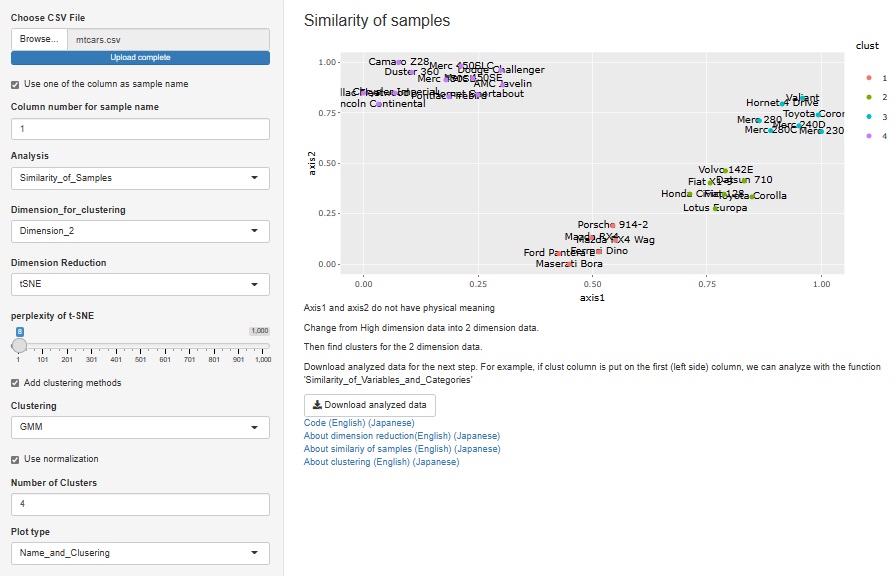
��ʃX�N���[�����s�����藈���肷��K�v���������̂ŁA ��@�̑I���Ƀ��W�I�{�^�����g���Ă����Ƃ���́A���ׂăZ���N�g�{�b�N�X�ɕς��܂����B
��ʃX�N���[�����[���ɂ͂Ȃ�܂��A���Ȃ���P���܂����B
 �@
�@
�N���X�^�[���͂����鎞�́A�K�����K����O�����Ƃ��čs���悤�ɂȂ��Ă����̂ł����A ���K�����邩�ǂ����͑I�ׂ�悤�ɂ��܂����B
�P�ʂ̈قȂ�ϐ����������Ă���ꍇ�͐��K�����K�v�ł����A �f�[�^�̌��X�̒l�̑傫�����d�v�ȏꍇ�͐��K��������Ƃ��ꂪ�����Ȃ��Ȃ�̂ŁA���K���͂��Ȃ������ǂ��ł��B
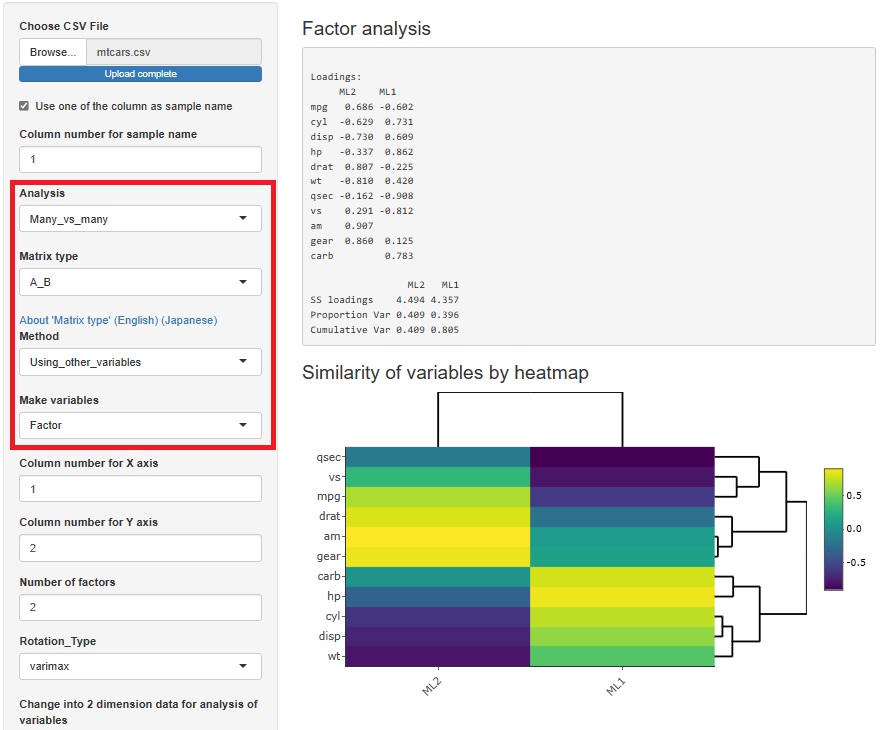
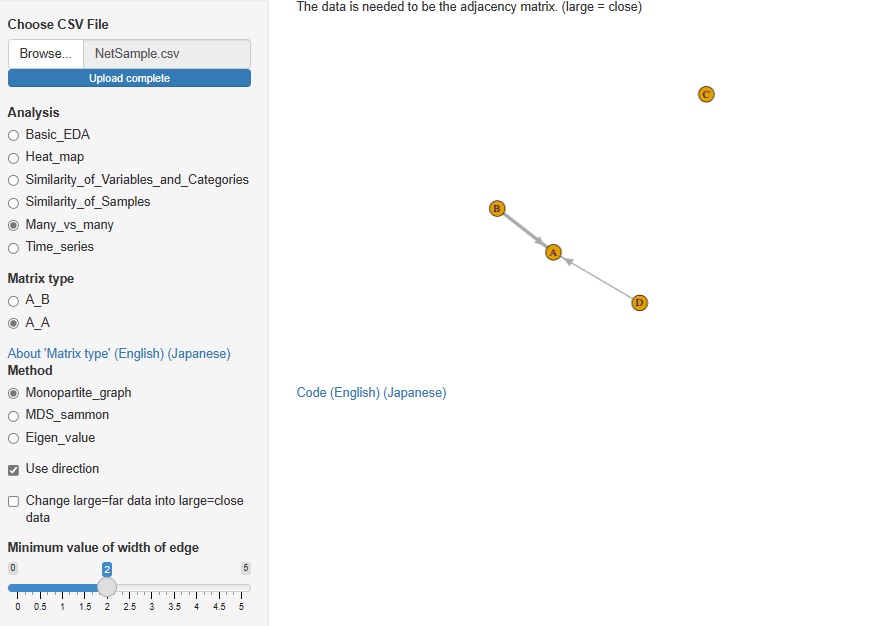
���Α��̕��� �̓��A A-B�^�̕��� �ɂ��ẮA �s�Ɨ�̍��ڂ́A���ړ��m�̗ގ��x�̕��� �ɓ����Ă�����@���AR-EDA1�ɓ���Ă����̂ł����A ����A A-A�^�̕��� ��lj����܂����B
�אڍs����X�^�[�g�ɂ������̃l�b�g���[�N�O���t�ɂ�镪�́A
�����s����X�^�[�g�ɂ������̑������ړx�\���@�iMDS�j�ɂ�镪�́A
���֍s����Ε]���̃f�[�^���X�^�[�g�ɂ������̌ŗL�l�A�ŗL�x�N�g���ɂ�镪�͂��ł���悤�ɂ��Ă���܂��B
 �@
�@
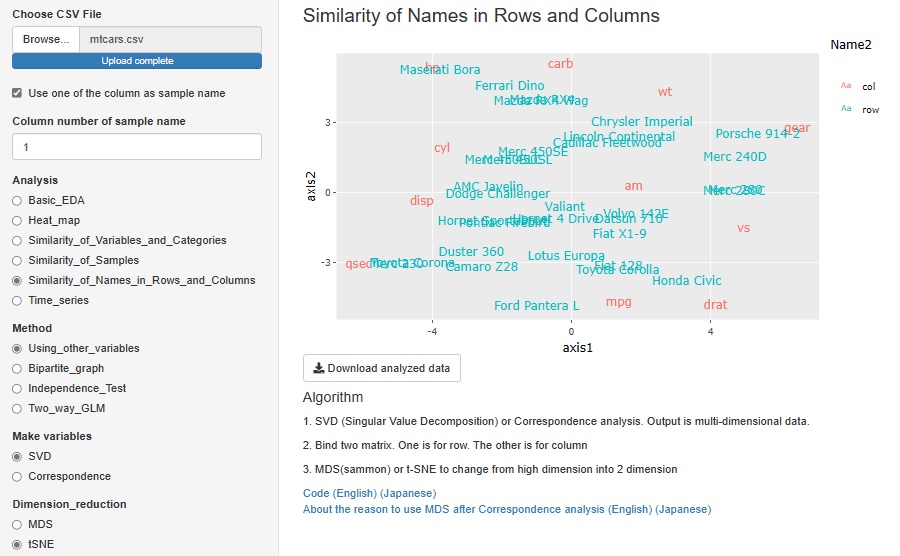
���R�����h��A�e�L�X�g�f�[�^�̕��͕��@�Ƃ��āA�s�Ɨ�̍��ڂ̃N���X�^�[���͂��悭�s���Ă���悤�ł��B SVD �iSingular Value Decomposition�F���ْl�����j�͂��̂ЂƂł����AR-EDA1�ɒlj����܂����B
���̃O���t�̐Ԃ����́A�e��̖��O�i�ϐ��̖��O�j�ŁA�����́A�e�s�̖��O�i�T���v���̖��O�j�ł��B �ϐ��Ɂu���x�v�Ɓu���x�v������ꍇ�ȂǁA�ϐ����ɕ����I�ȈӖ����قȂ�f�[�^�ł́A����ȕ��͂͂ł��܂���B �������A���ׂĂ̕ϐ����J�E���g�f�[�^�i�����ē����鐔�B�p�x�Ȃǁj��������A�_���������肵�āA�����I�ɓ����Ӗ��̏ꍇ�́A ���̕��@���g���܂��B
SVD�ƁA�R���X�|���f���X���͂��g����������悤�ɂ��Ă���܂��B SVD�́A���̒l�������Ă������܂����A�R���X�|���f���X���͂͐��̒l���������܂���B
SVD��R���X�|���f���X���͂Ő�������f�[�^�́A�������ɂȂ�܂����A
MDS�i�������ړx�\���@�j��t-SNE���g���āA2�����̎U�z�}�Ō�����悤�ɂ��Ă���܂��B
�u�R���X�|���f���X���́ESVD�v�̕Е��ƁA�uMDS�Et-SNE�v�̕Е���I�ׂ�̂ŁA�Q�~�Q���S�ʂ�̑g�������ł���悤�ɂ��Ă��܂��B
 �@
�@
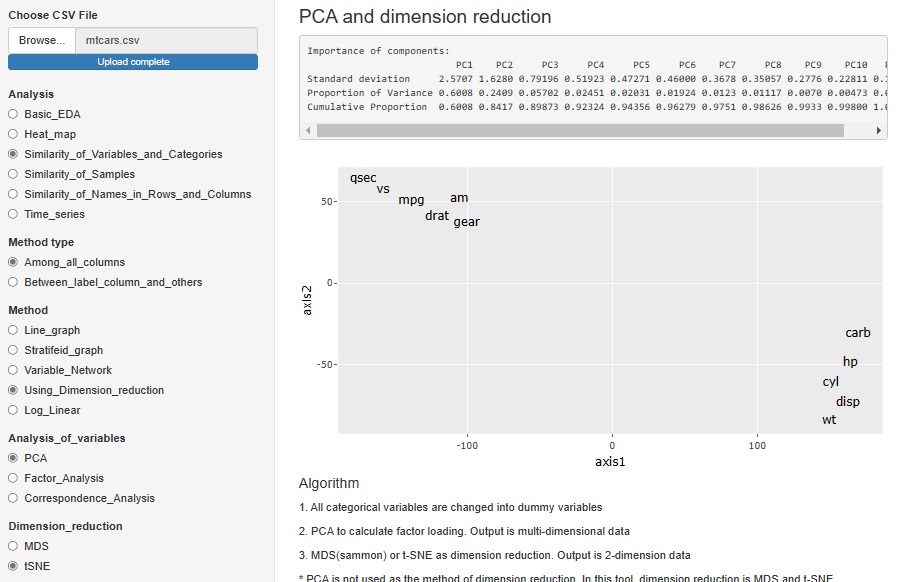
���̋@�\�́A���Ƃ��ƃR���X�|���f���X���͂�MDS�̑g�����̈���ł����B ����ASVD��t-SNE�𑝂₷���ƂŁA�S�ʂ�̕��@���ł���悤�ɂȂ�܂����B
PCA�i�听�����́j�AFactor analysis�i���q���́j�ACorrespondence analysis�i�R���X�|���f���X���́j�ŁA�ϐ��̗ގ����͂�����@�́A
���������Q�����Ō�����@�Ƃ��āAMDS�������̗p���Ă��܂������At-SNE�ł��ł���悤�ɂ��܂����B
 �@
�@
�uAnalysis�v�ɁuTime series(���n��j�v�������܂����B
���܂ł͎��n���͂���낤�Ƃ���ƁA�q�[�g�}�b�v��A�܂���O���t�����Ȃ������̂ł����A�����ԑ����Ă��܂��B
 �@
�@
�S�̂ɋ��ʂ��邱�ƂƂ��āA�u2021/10/19 13:30�v�̂悤�Ȏ����̃f�[�^�͎g��Ȃ��ł��B �����̃f�[�^�́A�\�L�̎d�����l�X�őS���ɑΉ�����c�[���͍�肫��Ȃ����߂ł��B ���̑���A�f�[�^�́u�P�������v�Ȃǂ̓��Ԋu�̎��ԂŎ��W���ꂽ���Ƃ�z�肵�Ă���̂ŁA �f�[�^�̌��Łu���ԁv�̕��͂��ł���悤�ɂ��Ă܂��B �P���Ԋu�̏ꍇ�A�un = 12�v�́u12���v�ł��B
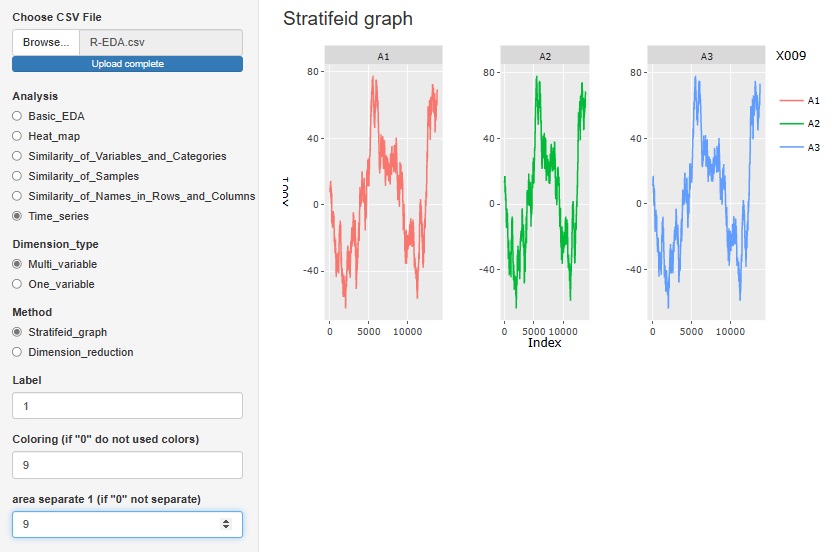
�uMulti_variable�i���ϗʁj�v�̒��́uStratifeid_graph(�w�ʃO���t�j�v�́A���ڂ������ϐ��̐܂���O���t�ł��B
���̕ϐ����g���ĐF����������A�O���t�����邱�Ƃ��ł��܂��B
 �@
�@
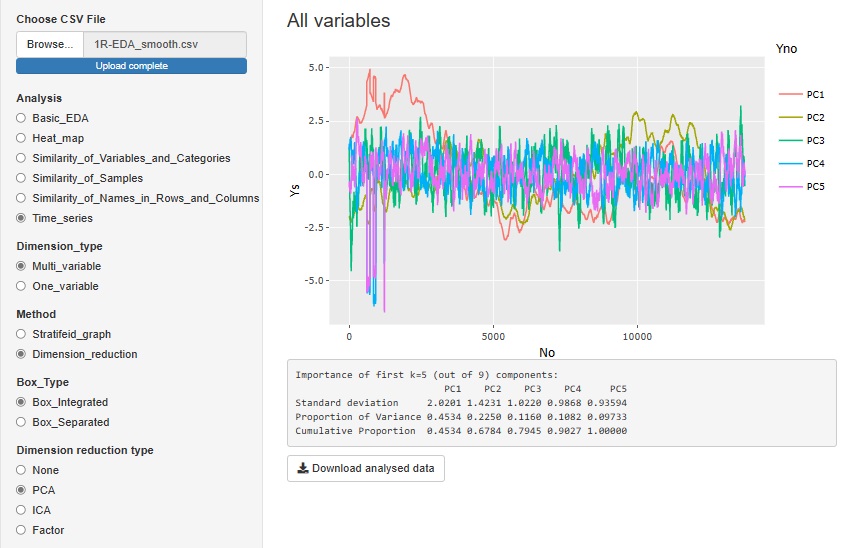
�uMulti_variable�i���ϗʁj�v�̒��́uDimension_reduction(�����팸�j�v�́A�����팸�̕��@�ŕϊ������ϐ��̑S�������邽�߂̃O���t�ł��B
���}�́A�uPCA�i�听�����́j�v��I�ꍇ�ł��B
�uICA�i�Ɨ��������́j�v��uFactor�i���q���́j�v�ł��ł��܂��B
�uNone�v��I�ԂƁA���̑��ϗʑS�����ꏏ�Ɍ���O���t�ɂȂ�܂��B
 �@
�@
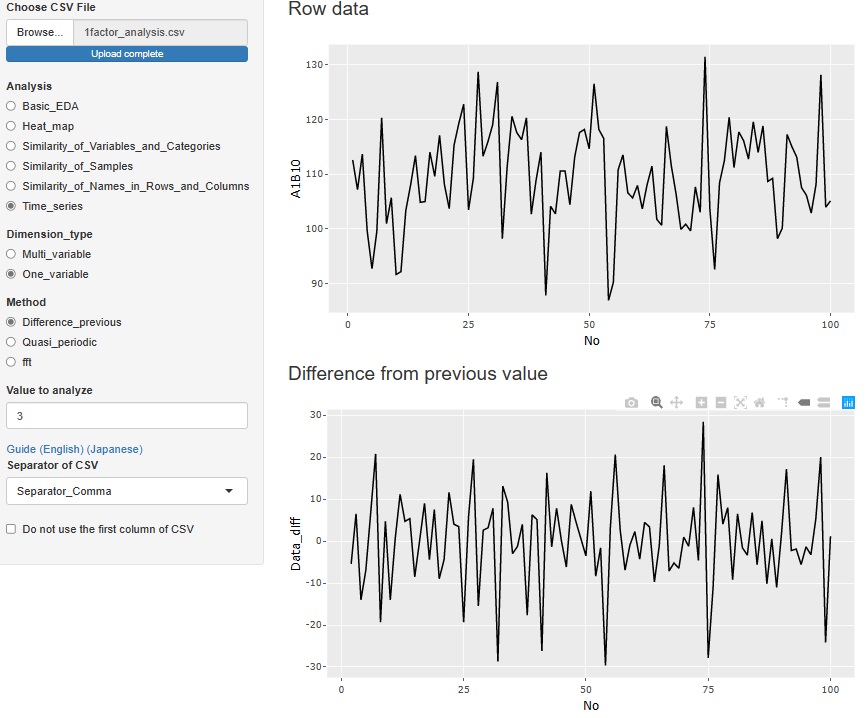
�uOne_variable�i��ϐ��j�v�̒��́uDifference_previous(�O�Ƃ̍��j�v�́A���O�̃f�[�^�Ƃ̍��i�����j�̕��͂ł��B
��ԏ�̃O���t�́A���̃f�[�^�ŁA���̉����������O���t�ɂ������̂ł��B
�����ɌX�����Ȃ��A�����_���ȏꍇ�́A
�����_���E�H�[�N���f��
�ƍl�����܂��̂ŁA�\�����鎞�́A���O�̒l����Ԋm���炵���\���l�ɂȂ�܂��B
 �@
�@
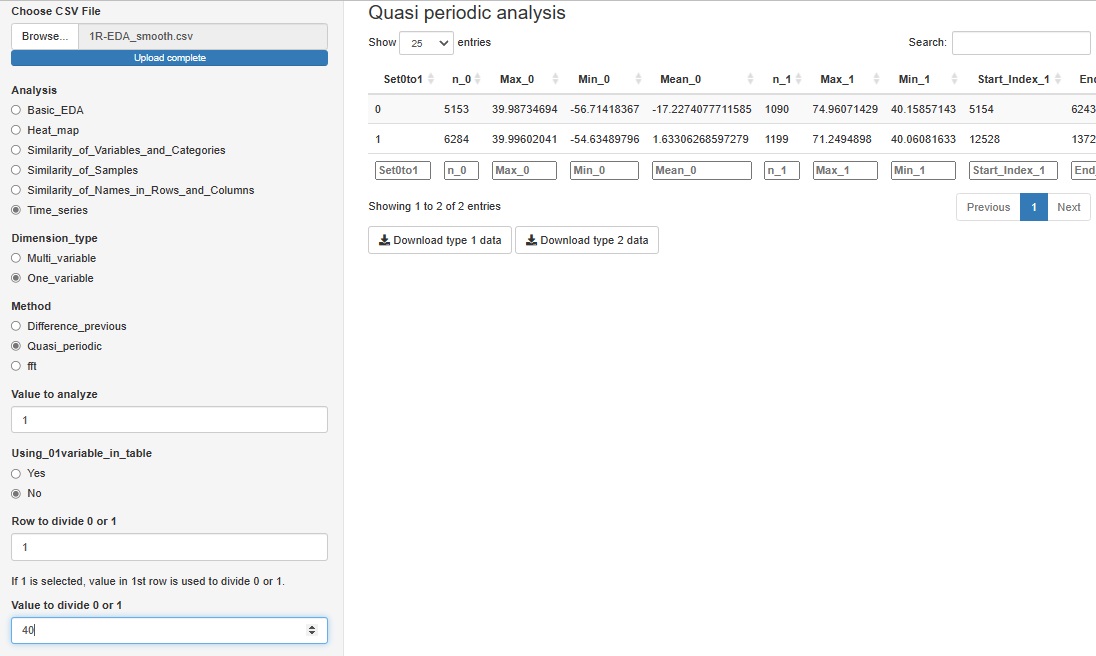
�uOne_variable�i��ϐ��j�v�̒��́uQuasi_periodic(�������j�v�́A�H��̃Z���T�[�f�[�^�̂悤�ɁA
�J��Ԃ��͂�����̂́A�����̒��������ł͂Ȃ��f�[�^�̕��͂����邽�߂̃c�[���ł��B
���̋@�\�́A�O���t�̏o�͂͂Ȃ��A
1.5���f�[�^�̉��
��A
�Q���f�[�^�i�����ʁj�̉��
�����邽�߂̃f�[�^���_�E�����[�h�ł���悤�ɂȂ��Ă��܂��B
�K�v�ɉ����āA���̃f�[�^������ɕ��͂Ɏg�����Ƃ�z�肵�Ă��܂��B
�����������A�P�ƂO�̐����ŕ\����Ă���ϐ�������A������g�����Ƃ��ł��܂��B
�����������ϐ����Ȃ��ꍇ�A����̕ϐ��ɂ��āA�u�P��ڂ��A40���傫����P�A40�ȉ��Ȃ�O�v�Ƃ����悤�ɂ��āA���������ϐ�����邱�Ƃ��ł��܂��B
 �@�@
�@�@
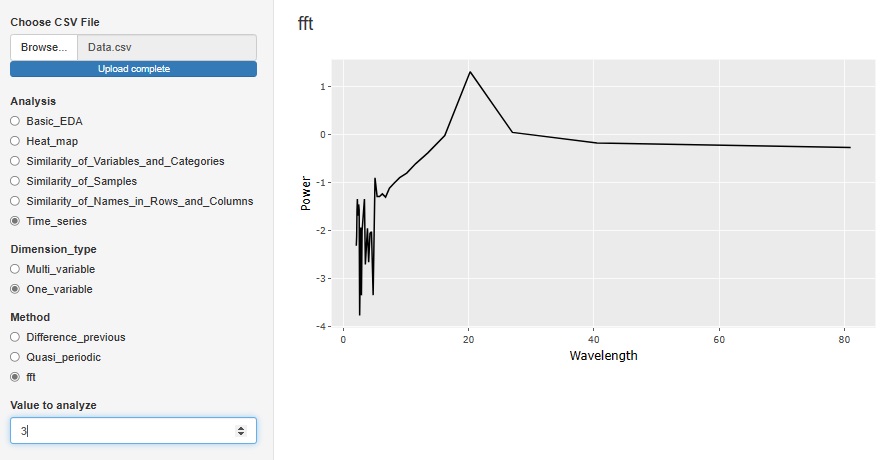
�uOne_variable�i��ϐ��j�v�̒��́ufft(�����t�[���G�ϊ��j�v�́A
�X�y�N�g�����
�̃c�[���ł��B���m�Ȏ�����������ꍇ�̕��͕��@�ɂȂ�܂��B
�����́AWavelength�i�g���j�ɂ��Ă���܂��B
���}�̏ꍇ�́A�g����20�̂Ƃ���Ƀs�[�N������܂��̂ŁA20�s�����Ɏ������̂���f�[�^�ł��邱�Ƃ��킩��܂��B
 �@
�@
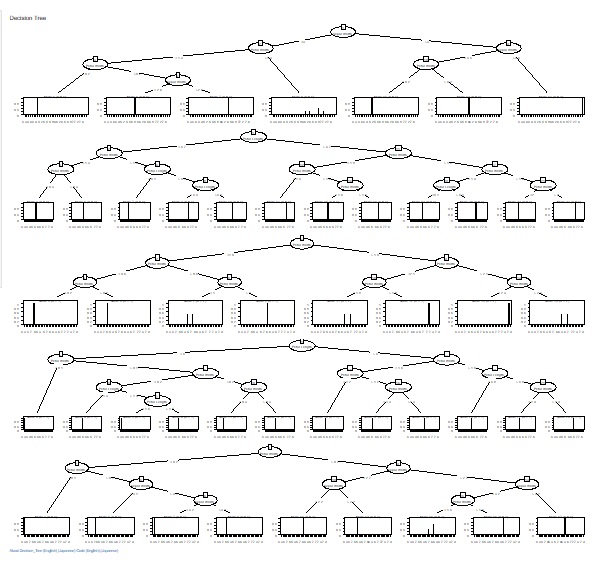
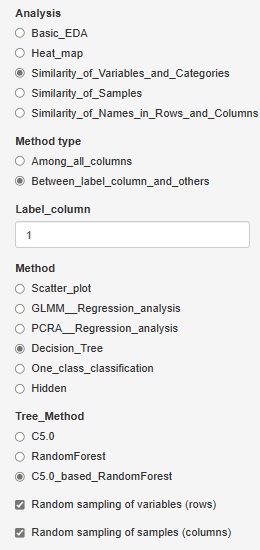
�uDecision_Tree�i����j�v�ɁA�uC5.0_based_RandomForest�iC5.0���g���������_���t�H���X�g�j�v��lj����܂����B
�uC5.0�v�ł́A�͂P�ł��܂����A����͑S�ϐ��A�S�T���v�����g���č���܂��B
C5.0_based_RandomForest�ł́A�ϐ���T���v���̂P���ɂ��āA�����̑g������I�Ԃ��ƂŁA�����̖����܂��B ����ɂ���ăf�[�^�̑��l����A�����悤�Ȍ��ʂɂȂ�ϐ����킩��悤�ɂȂ�܂��B
�P���̃f�[�^�̑I�ѕ��́A�����_���T���v�����O�ł��B �s����̕������̐���I�Ԃ悤�ɂ��Ă���܂��B �Ⴆ�A10000�s�̃f�[�^�Ȃ�A100�s���I��܂��B
�uRandom sampling of samples (columns)�v�Ƀ`�F�b�N�����āA �uRandom sampling of variables (rows)�v�̃`�F�b�N���O���ƁA�T���v���͂P�����g���āA�ϐ��͑S���g���`�ŁA�����̖����܂��B ����́u�o�M���O�v�Ƃ��������Ă����@�ɂȂ�܂��B
�t�ɁuRandom sampling of samples (columns)�v�̃`�F�b�N���O���āA �uRandom sampling of variables (rows)�v�Ƀ`�F�b�N������ƁA�ϐ��͂P�����g���āA�T���v���͑S���g���`�ŁA�����̖����܂��B �T���v���������Ȃ��ꍇ��A���ʊW�̕��͂ł́A���̂����̕����m�肽�����Ƃɓ��B���₷���Ȃ�܂��B
 �@
�@
 �@
�@
�������鎞�ׂ̖̍����́A�f�t�H���g�ɂ��C���ɂ��Ă����̂ł����A����Ȗi�}�����ꂪ�ׂ����j�ɂȂ邱�Ƃ�����܂��B ���ʊW�̕��͂ł́A�R�Ԗڂ��炢�܂ł̎}�����ꂪ�ǂ��Ȃ�̂����d�v�ŁA����Ȗ͕s�v�Ȃ��Ƃ������ł��B �܂��A����Ȗ�OK�ɂ���ƁA�v�Z���Ԃ����ɒ������Ƃ�����܂��B ����ɁA����Ȗ́A�ߊw�K�Ƃ������邱�Ƃ�����A���o�X�g�ł͂Ȃ��̂Ŏg���ɂ����ł��B
�����ŁA�}�������̍ŏ��̑傫����ݒ�ł���悤�ɂ��܂����B
�uUse minimum size of splits�v�Ƀ`�F�b�N������ƁA�ݒ�ł���悤�ɂȂ�܂��B
�`�F�b�N���O���ƁA�f�t�H���g�ɂ��C���ɂȂ�܂��B
�Ⴆ�A�uRatio of the number of minimum size�v���u0.1�v�ɂ���ƁA�ŏ��ɂȂ�}������́A�S�̂�0.1�ɂȂ�܂��B
1000�s�̃f�[�^�ł�����A100�����������͂Ȃ�Ȃ��Ȃ�܂��B
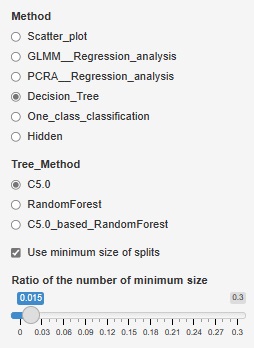
���̂Q�̐}�́A�����f�[�^�ɑ��āA�ݒ�l��ς����ꍇ�̗�ł��B
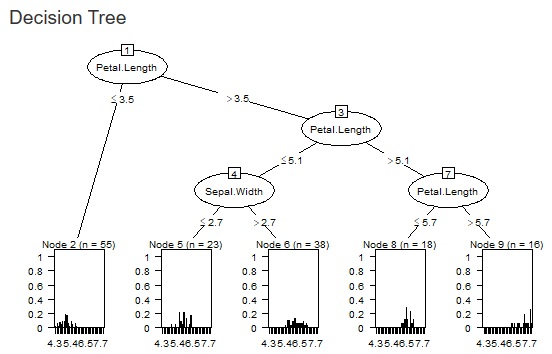 �@
�@
���܂ł́A�uSimilarity_of_Variables_and_Categories�i�ϐ��ƃJ�e�S���̗ގ��x�j�j�v�ƁA �uSimilarity_of_Names_in_Rows_and_Columns�i�s�Ɨ�̖��O�̗ގ����j�v�̂��ꂼ��̒��ɁA �q�[�g�}�b�v���g���āA�f�[�^�̕\�S�̂�����������@�����Ă��܂����B ���ꂼ��ŏ����@�\��ς��Ă��܂����B
�f�[�^�̕\�S�̂�����������@�́A�uSimilarity_of_Samples�i�T���v���̗ގ��x�j�v�ł��𗧂̂ł����A�����Ă��܂���ł����B
�f�[�^�̕\�S�̂�����������@�́AEDA�̊�{�ɂȂ���̂ł����A�R��ނ�Similarity�̑S���͂ł�����@�Ƃ��Ă����̕��@�Ƃ͈Ⴂ�܂��̂ŁA
�uHeat_map�i�q�[�g�}�b�v�j�v�́A�R��ނ�Similarity�̕��͂���Ɨ������ĂЂƂ܂Ƃ߂ɂ��܂����B
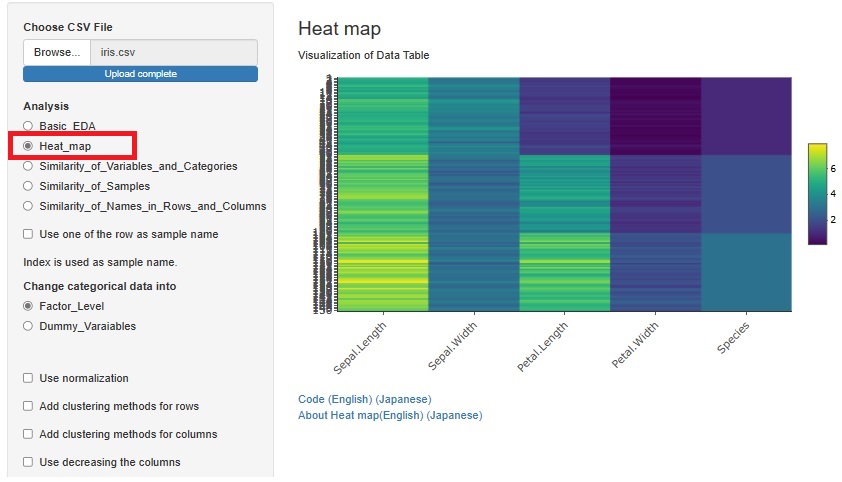
�uAdd clustering methods for rows�v�Ƀ`�F�b�N������ƁA�����ϐ����߂��ɂȂ�悤�ɕ��ѕς����܂��B
�uAdd clustering methods for columns�v�Ƀ`�F�b�N�����邱�ƂŁA�����T���v�����߂��ɂ��邱�Ƃ��ł��܂��B
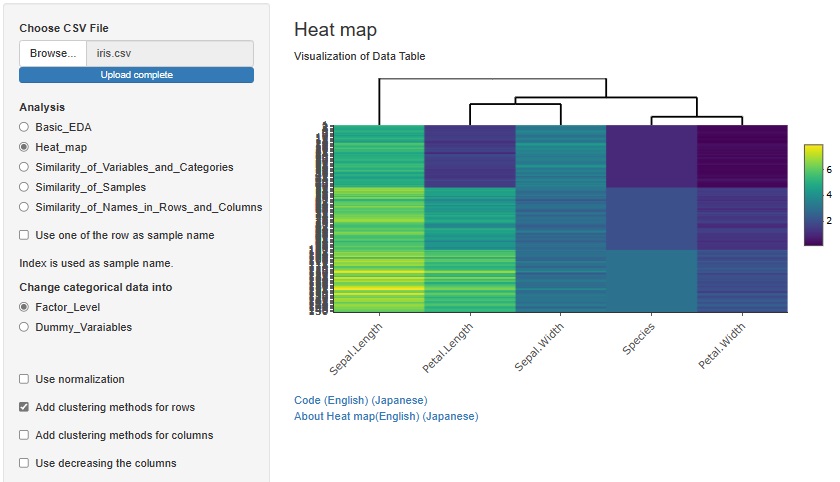
�����T���v�����߂��ɂ�����@�́A�����ЂƂ���܂��B
�uUse decreasing the columns�i�s�̍~�����g���j�v�Ƀ`�F�b�N������ƁA�C�ӂ̕ϐ��ɂ��č~���ŕ��ׂ��܂��B
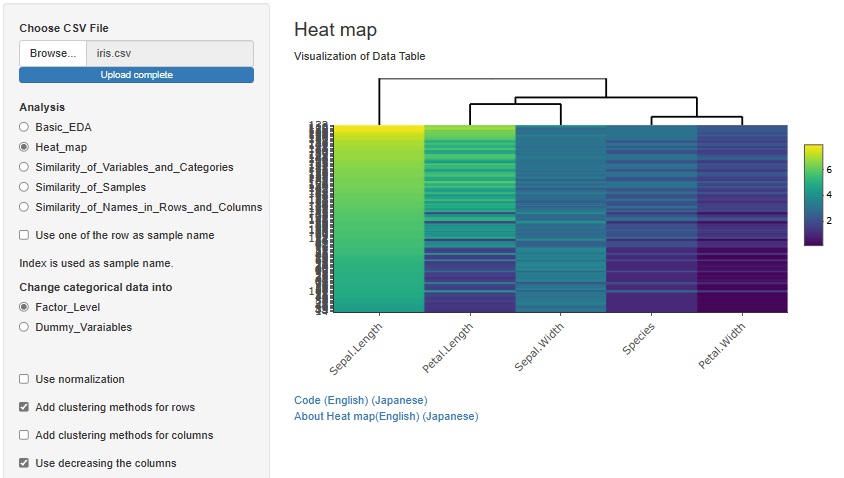
�uHeat_map�i�q�[�g�}�b�v�j�v�A�uSimilarity_of_Samples�i�T���v���̗ގ����j�v�A�uSimilarity_of_Names_in_Rows_and_Columns�i�s�Ɨ�̖��O�̗ގ����j�v�̂R�̕��͂̋@�\�ɂ́A���܂ŁA�u�f�[�^�ɂ́A�T���v�����̗Ȃ���Ȃ�Ȃ��v�A�u�T���v�����̗�͂P��ڂłȂ���Ȃ�Ȃ��v�A�Ƃ����O����܂����B
����A���̂Q�̑O���s�v�ɂ��܂����B
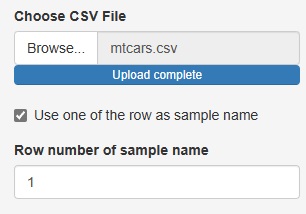
�uUse one of the row as sample name�v�̃`�F�b�N���O���ƁA�T���v�����̗Ȃ��ꍇ�ɁA�s�ԍ����T���v�����̑���ɂ��āA���͂��邱�Ƃ��ł��܂��B
�uRow number of sample name�i�T���v�����̗�ԍ��j�v�ɓ��ꂽ�����̗T���v�����Ƃ��Ĉ����܂��B
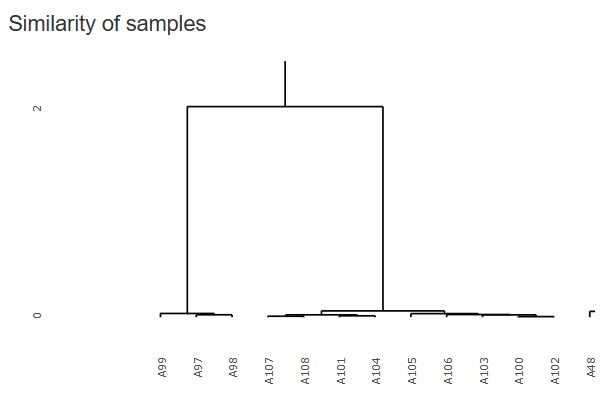
�K�w�I�ȕ��@�ɂ��N���X�^�[���͂́A�T���v���̎�ނ����Ȃ����͗ǂ��̂ł����A������x�����Ȃ�ƁA�O���t�Ɏ����d�Ȃ�悤�ɂȂ�A ��Ǖs�\�ɂȂ�܂��B
���̂��߁AR-EDA1�ɂ͓���Ă��Ȃ������̂ł����A�C���^���N�e�B�u�ȃ^�C�v�̃O���t�ɂ���̂Ȃ�A��Ǖs�\�Ƃ������Ƃ��Ȃ��Ȃ�܂��̂ŁA �lj����܂����B
�uSimilarity_of_Samples�i�T���v���̗ގ����j�v
���uDimension_All"�i�S�����j�v
�Ɛi���ɂ���uhclust�v�ɂȂ�܂��B
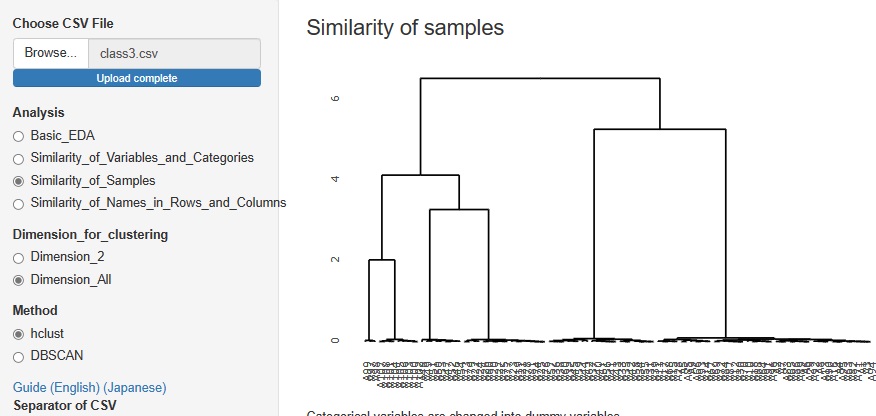
���}���C���^���N�e�B�u�̋@�\���g���āA�ꕔ���g�債�����̂ł��B
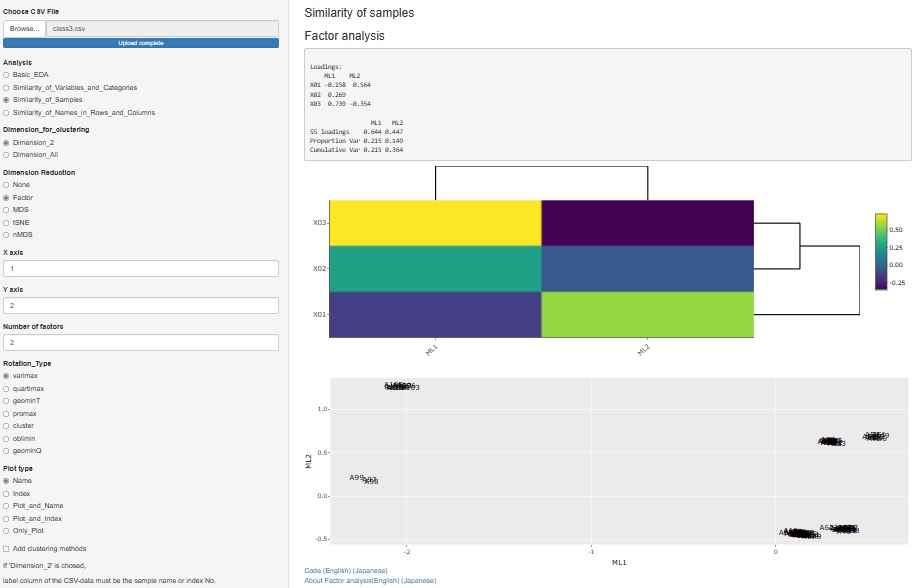
2021/09/25�Ɉ��q���͂̃����[�X�����܂������A�ϐ��̊W�͂��邽�߂̋@�\�Ƃ��č���Ă��܂����B ���̂��߁A�uSimilarity_of_Variables_and_Categories�i�ϐ���J�e�S���̗ގ����j�v�̒��ɑg�ݍ��܂�Ă��܂����B
���q���͂́A�T���v���̗ގ��������q�Ƃ̊W���܂߂Ē��ׂ������ɂ��g���܂��̂ŁA���̂��߂̋@�\�����܂����B
�uSimilarity_of_Samples�i�T���v���̗ގ����j�v
���uDimension_2"�i2�����j�v
�Ɛi���ɂ��鎟���팸�̎�ނɁA�uFactor�i���q�j�v��lj����܂����B
�Q�����U�z�}�̎����A���q�ɂȂ�܂��B
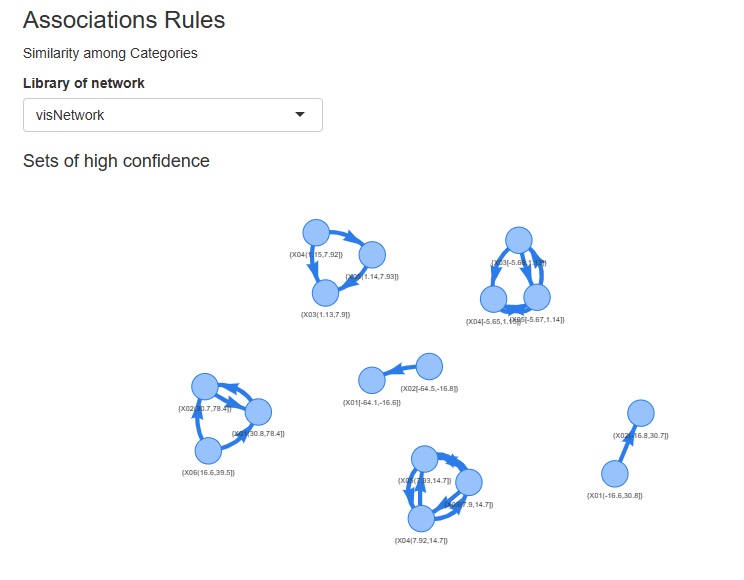
�قڂ��ׂẴO���t���A�C���^���N�e�B�u�ȃ^�C�v�ɕς��܂����B �����ڂ͓����ł��A�������ꏊ�����g��\��������A�}�E�X�ŌX�̃v���b�g�̏����m�F�ł����肵�܂��B �l�b�g���[�N�O���t�̏ꍇ�́A�O���t���܂�ŃO���O���������܂��B
�U�z�}��q�X�g�O�����Fggplotly��plotly��
�q�[�g�}�b�v�Fheatmaply�ɕύX
�l�b�g���[�N�O���t�F�����O���t��network3D�A�L���O���t��visnetwork
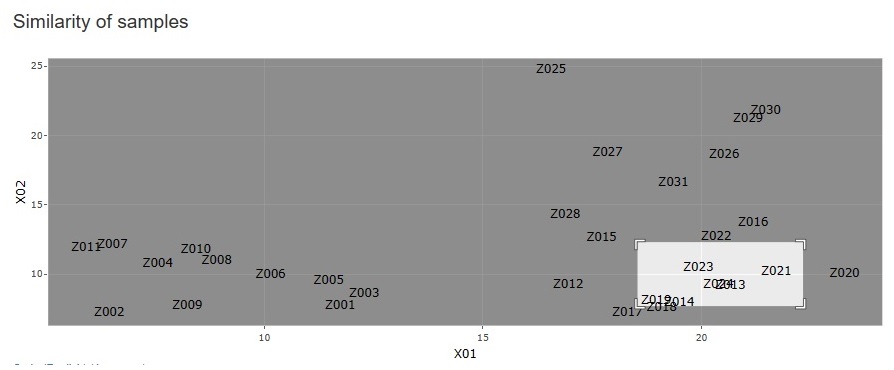
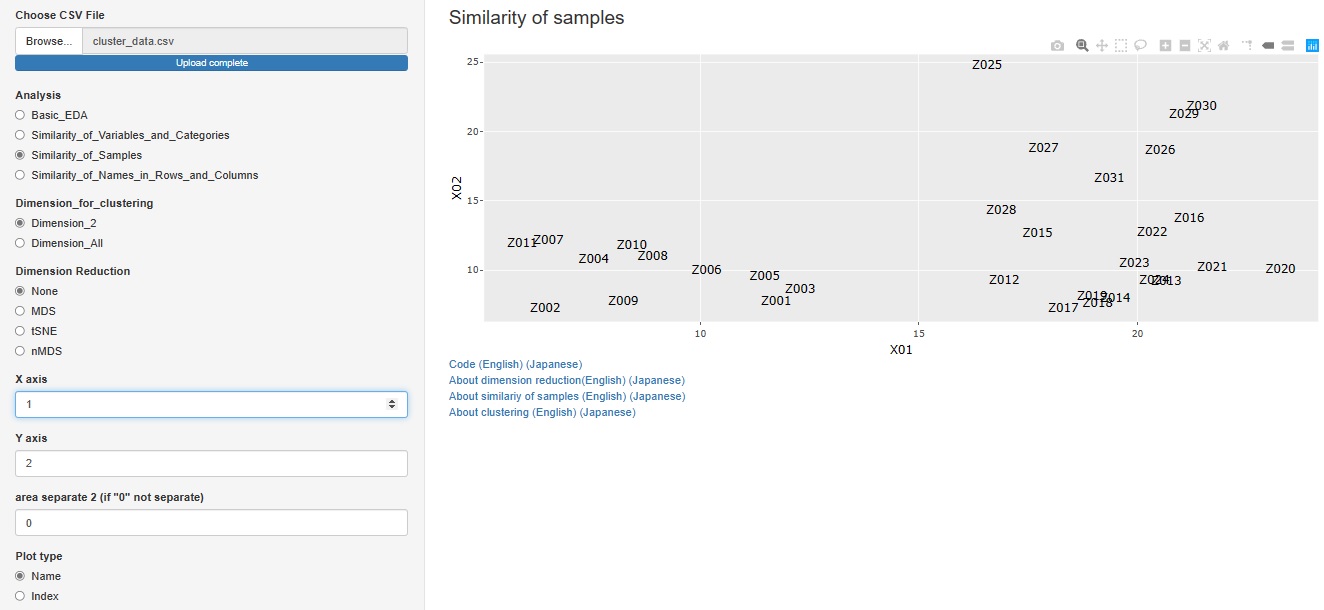
�uSimilarity_of_Samples�i�T���v���̗ގ����j�v
���uDimension_2"�i2�����j�v
�Ɛi���ɂ��鎟���팸�̎�ނɁA�uNone�i�Ȃ��j�v��lj����܂����B
�C�ӂ̂Q�̕ϐ��ɂ��āA�T���v�����̎U�z�}�����܂��B
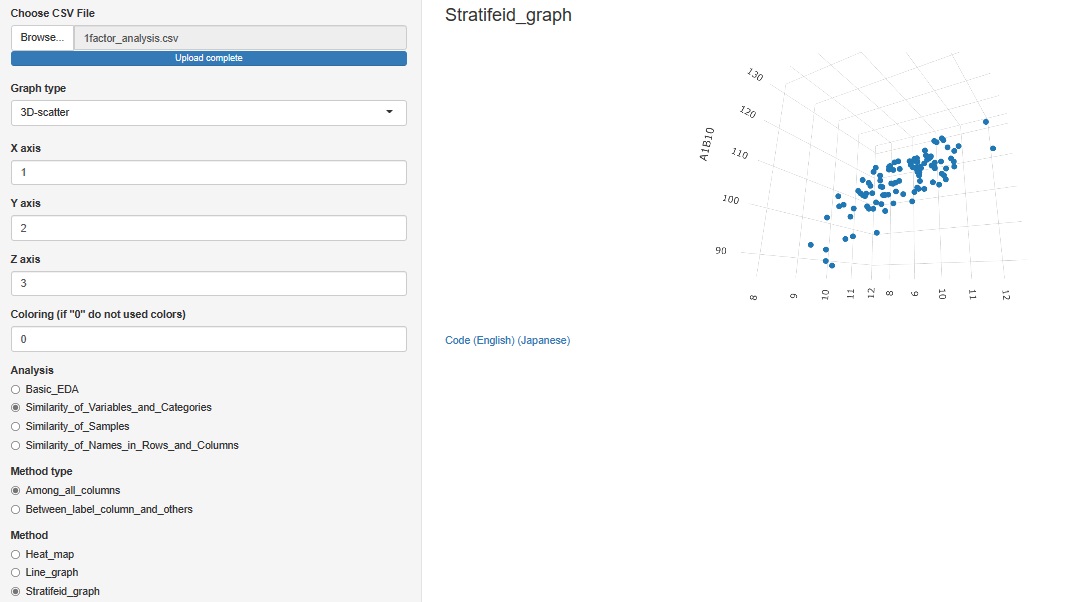
�uSimilarity_of_Samples�i�T���v���̗ގ����j�v
���uAmong_all_columns�i���ׂĂ̗m�j�v
���uStratifeid_graph�i�w�ʃO���t�j
�Ɛi���ɂ���O���t�̎�ނɁA�u3D-scatter�i�R�����U�z�}�j�v��lj����܂����B
�R�����̎��ȊO�ŁA�w�ʂł���̂́A�F�����ł�
�Q�����U�z�}�̂悤�ɃO���t�̕����͂ł��܂���B
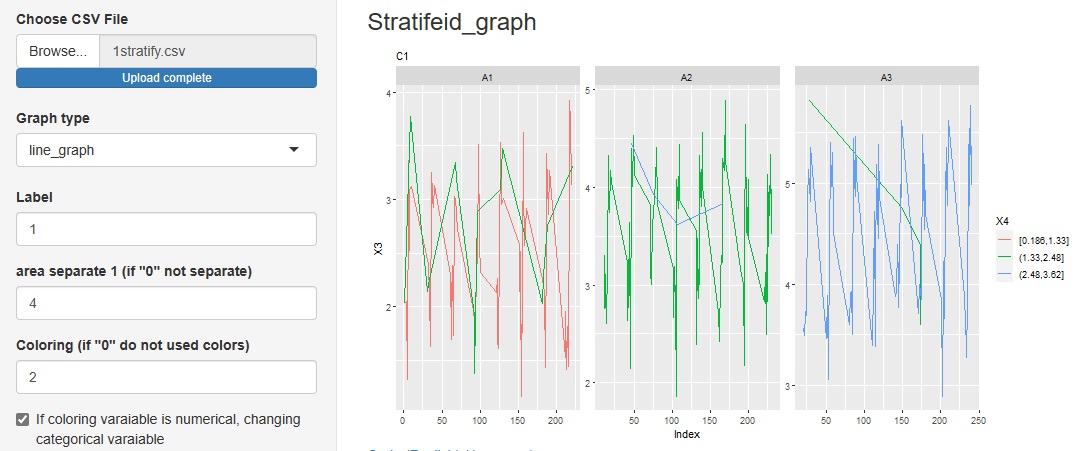
�uSimilarity_of_Variables_and_Categories�i�ϐ���J�e�S���̗ގ����j�v
���uDimension_2�i�Q�����j�v
�Ɛi���ɂ��鎟���팸�̎�ނɁA�uline_graph�i�܂���O���t�j�v��lj����܂����B
���x���̕ϐ��̕ω��̒��ɁA���̕ϐ��̃J�e�S�����ǂ̂悤�ɓ����Ă���̂����킩��܂��B

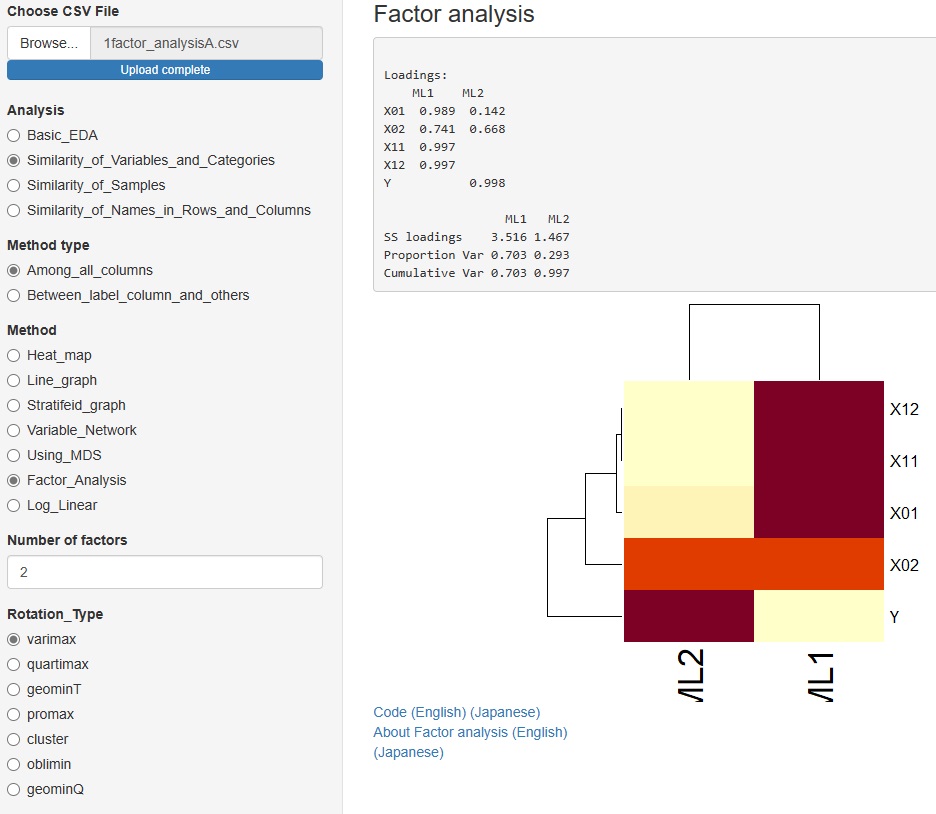
�uSimilarity_of_Variables_and_Categories�i�ϐ���J�e�S���̗ގ����j�v
���uAmong_all_columns�i���ׂĂ̗m�j�v
�Ɛi���ɂ���Method�i���@�j�ɁA�uFactor_Analysis�i���q�����j�v��lj����܂����B
�f�[�^�Ƃ��Č����Ă���ϐ��̔w��ɋ��ʈ��q�����肵�āA���ꂪ�ǂ̂悤�Ƀf�[�^�Ɋւ���Ă���̂��ׂ邱�Ƃ��ł��܂��B
��]�́A�V��ނ���I�ׂ܂��B
�uSimilarity_of_Variables_and_Categories�i�ϐ���J�e�S���̗ގ����j�v
���uBetween_label_column_and_others�i���x���̂Ƒ��̕ϐ��̊W�j�v
���uStratifeid_graph�i�j
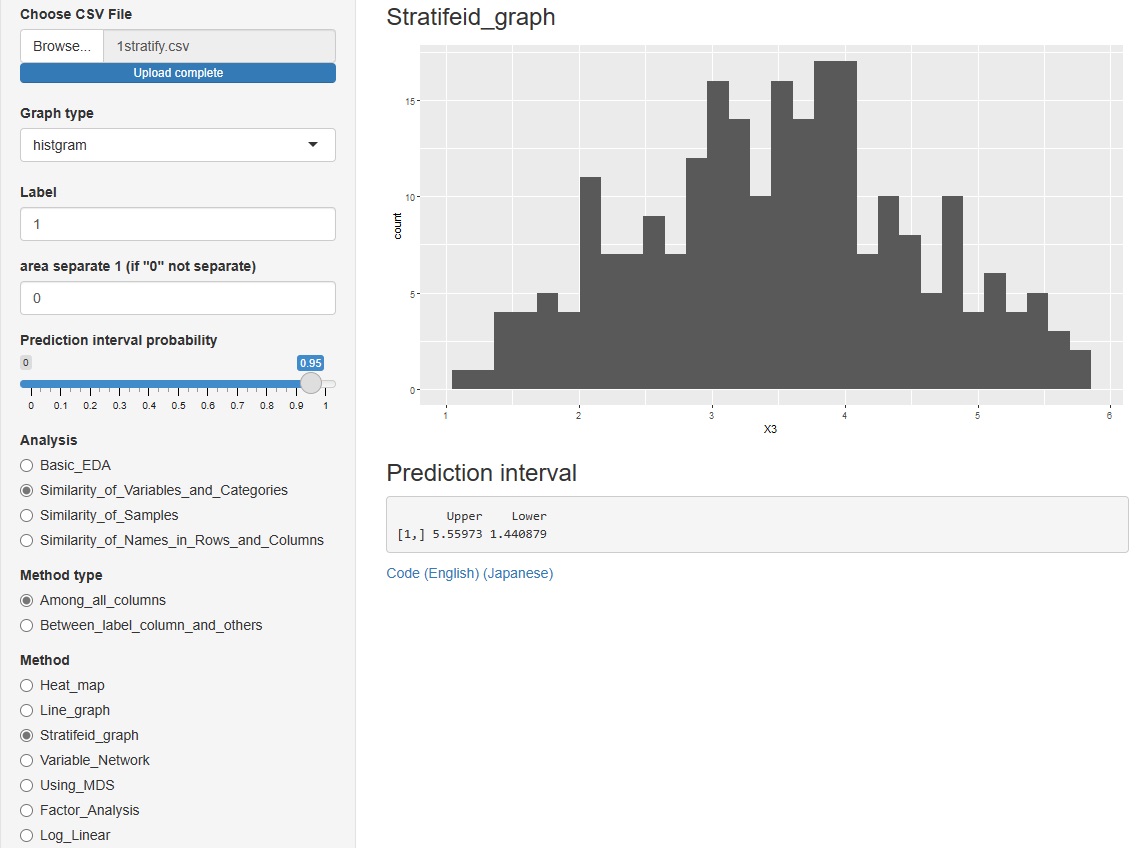
�Ɛi���ɂ���uhistgram�i�q�X�g�O�����j�v�Ɓuscatter�i�U�z�}�j�v�̂��ꂼ����\��������o���悤�ɂ��܂����B
�������A��������O���t��w�ʂ������ɂ́A�v�Z����܂���B
�q�X�g�O�����́A��Ԃ������ŕ\������܂��B
�U�z�}�́A�O���t�ɐԂ����ŕ\������܂��B
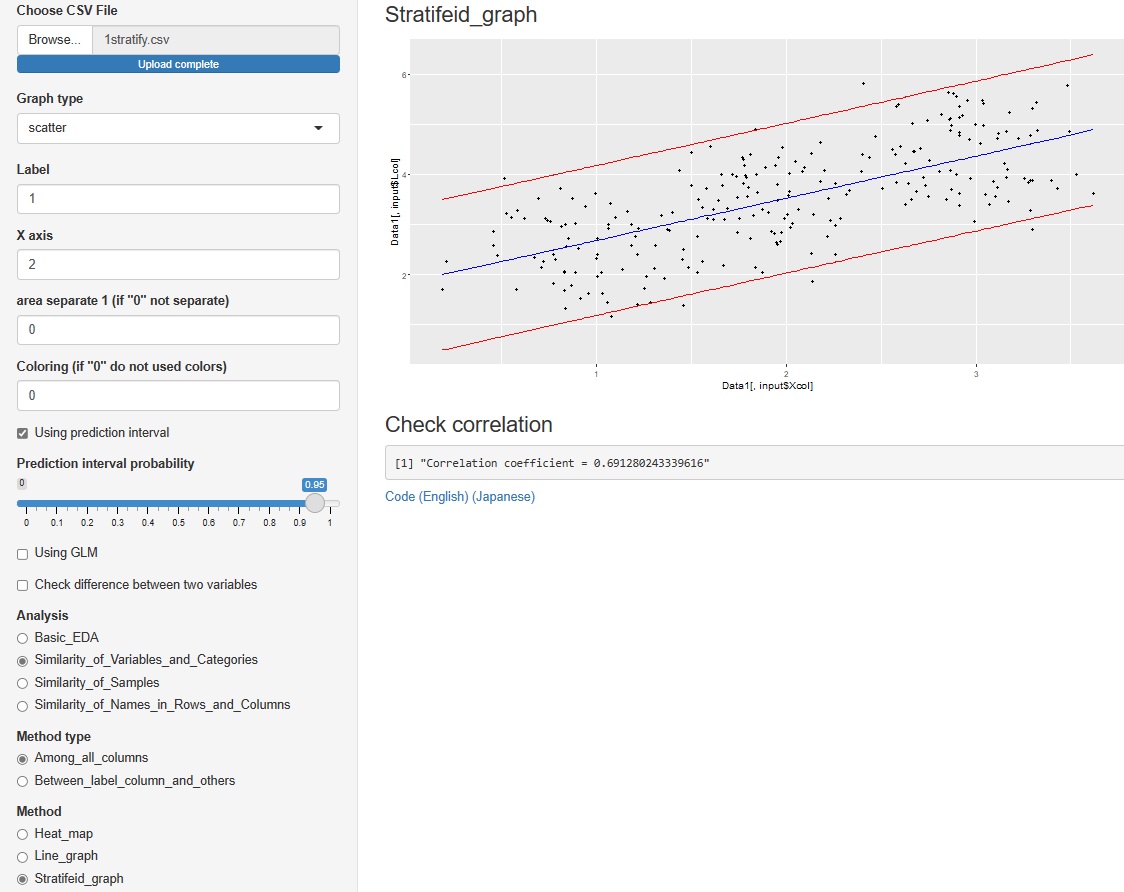
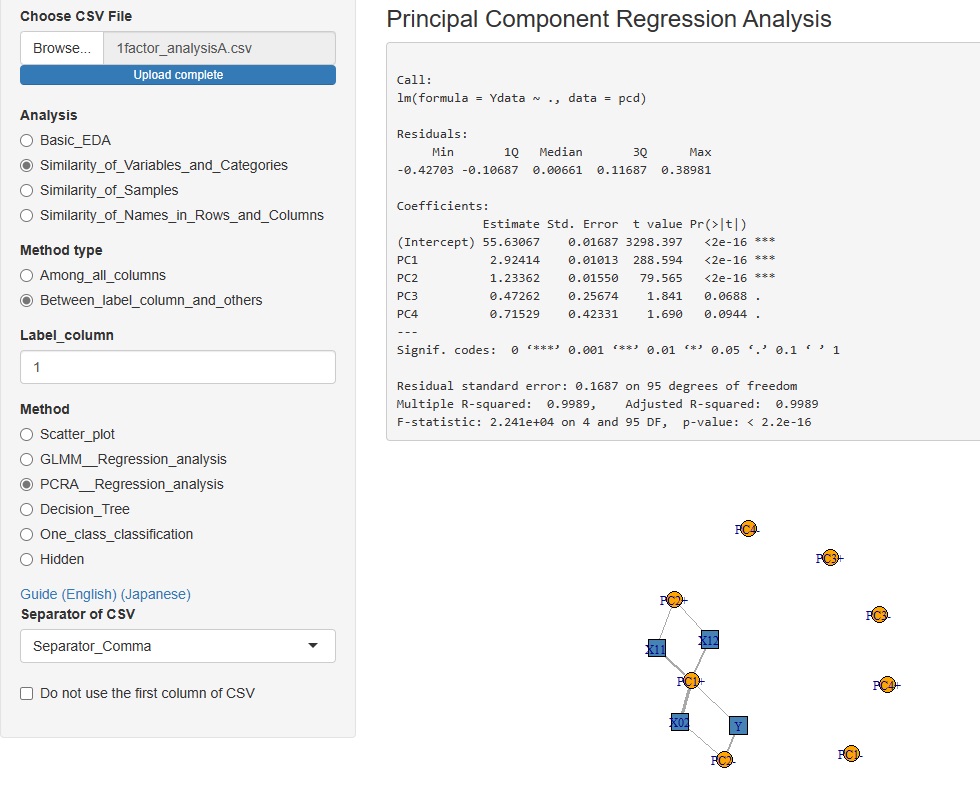
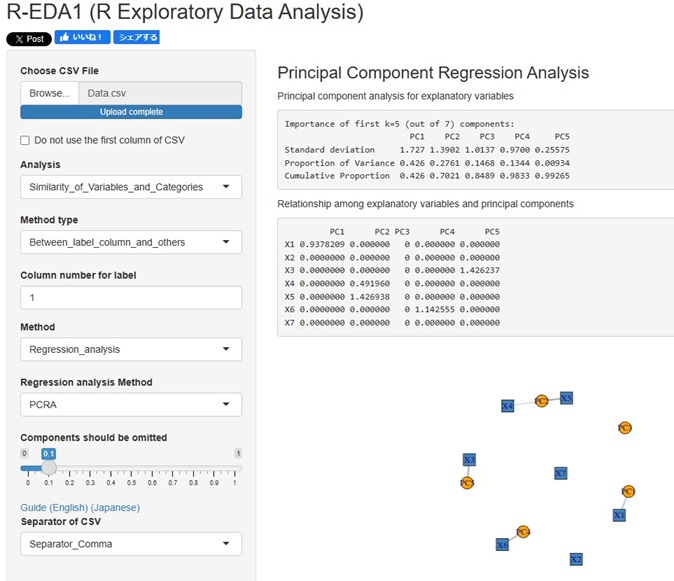
�uSimilarity_of_Variables_and_Categories�i�ϐ���J�e�S���̗ގ����j�v
���uBetween_label_column_and_others�i���x���̕ϐ��ƁA���̕ϐ��̊W�j�v
�Ɛi���ɂ���Method�i���@�j�ɁA�uPCRA__Regression_analysis�i�听����A�����j�v��lj����܂����B
�����ϐ��Ǝ听���̑��֊W�́A�l�b�g���[�N�O���t�Ŋm�F�ł���悤�ɂ��Ă��܂��B