例えば、上のグラフのように、カテゴリが５つあっても、全部が一直線上に重なる感じなら、線形混合モデルは不要で、 普通の 単回帰分析 で十分なのですが、こうではない場合を扱えるようになります。
一般化線形混合モデル（Generalized Linear Mixed Model：GLMM）は、一般化線形モデルと、線形混合モデルを合体させたものです。
一般化線形モデル のページには 単回帰分析 の発展版としての話がまとまっています。
一般化線形モデル の 重回帰分析 の発展版としての使い方で、一般化線形モデルのちょっと変わった使い方として、 対数線形分析 があります。
線形混合モデルも
重回帰分析
の拡大版です。
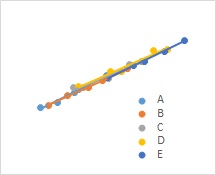
例えば、上のグラフのように、カテゴリが５つあっても、全部が一直線上に重なる感じなら、線形混合モデルは不要で、
普通の
単回帰分析
で十分なのですが、こうではない場合を扱えるようになります。
カテゴリ毎に、傾きや切片が異なる時は、カテゴリ毎に 層別 して（データを分けて）分析する手がありますが、 線形混合モデルでは、ひとつのモデルでこのようなケースを扱います。
カテゴリ毎に異なる効果が「変量効果」、共通の効果が「固定効果」です。 具体的には、変量効果はカテゴリの数だけ傾きや切片の係数があるものです。 固定効果は全カテゴリで共通の係数になります。
切片が変量効果、傾きが固定効果のモデルが当てはまるのはいくつかあります。
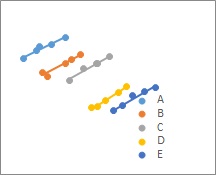
１つめの場合は、全データで単回帰分析をすると、負の相関になるのに、カテゴリ毎に見ると、正の相関になっている場合です。
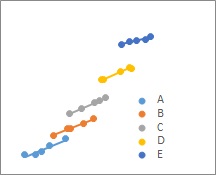
２つめの場合は、全データの単回帰分析と、各カテゴリの傾きはそんなに変わらないのですが、各カテゴリが平行している場合です。
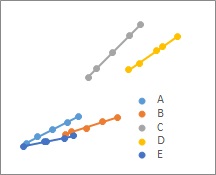
３つめの場合は、全データの単回帰分析では、相関ありとならないのに、各カテゴリでは高い相関がある場合です。
切片が固定効果、傾きが変量効果のモデルが当てはまるのは、放射状にデータが広がっている場合があります。
線形混合モデルの使い道としては、「カテゴリ毎に傾きや切片が異なる」の他に、 「繰り返し測定したデータのセットが複数ある」もあります。
この場合は、「データのセット毎にカテゴリが違う」と考えて、カテゴリを表す質的変数を追加することで、線形混合モデルが使えるようになります。
専用ソフトを使わずに線形混合モデルを実行しようとすると、 ダミー変数 を使うことになります。
広義の数量化Ⅰ類 のページに、データの質的な違いによって、傾きと切片の異なる回帰直線が複数ある状態を作る話がありますが、 これと線形混合モデルは同じです。
一般化線形混合モデルは、伝統的な統計学や多変量解析の延長にあるものです。 一般化線形混合モデルよりももっと複雑な分布を扱いたい場合は、 ベイズ統計 の延長にある 階層ベイズ の世界になってきます。
計量経済学では、線形混合モデルによる分析は、「パネルデータ分析」という名前で解説されていることが多いです。
パネルデータ分析では、X軸は時間で、時系列分析の一種になっています。
Rの実施例は、 Rによる一般化線形混合モデル のページにあります。 一般化線形モデルは、 Rによる対数線形分析 にもあります。
R-EDA1 では、一般化線形モデル、線形混合モデル、一般化線形混合モデルが使えます。
「Stratifeid_graph（層別のグラフ）」を選んで、「scatter（散布図）」を選ぶと、散布図を描くために選んだ変数を使って、 LMM（線形混合モデル）、GLMM（一般化線形混合モデル）の結果が、散布図の下に出てきます。
GLMMの結果だけだと、R-squared（決定係数：相関係数の二乗）の数字が計算されないので、LMMを入れています。
また、R-EDA1では、上記のRの実施例の書き方だとなぜかエラーが出るので、数量化I類のやり方で、交互作用項の入ったモデルを作っています。
step関数を使って、有意でない項は削除したモデルが作られるようにしています。
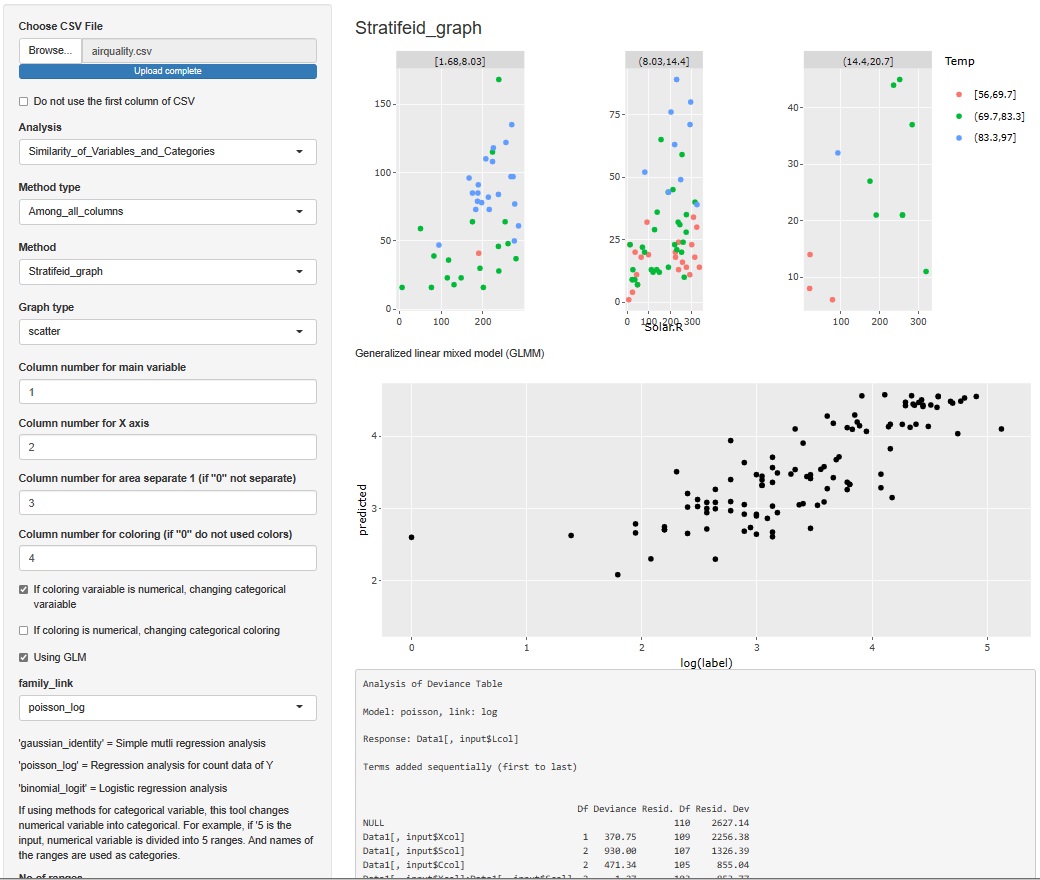
散布図とセットにした分析の時は、散布図に使っている変数がモデルに入ります。
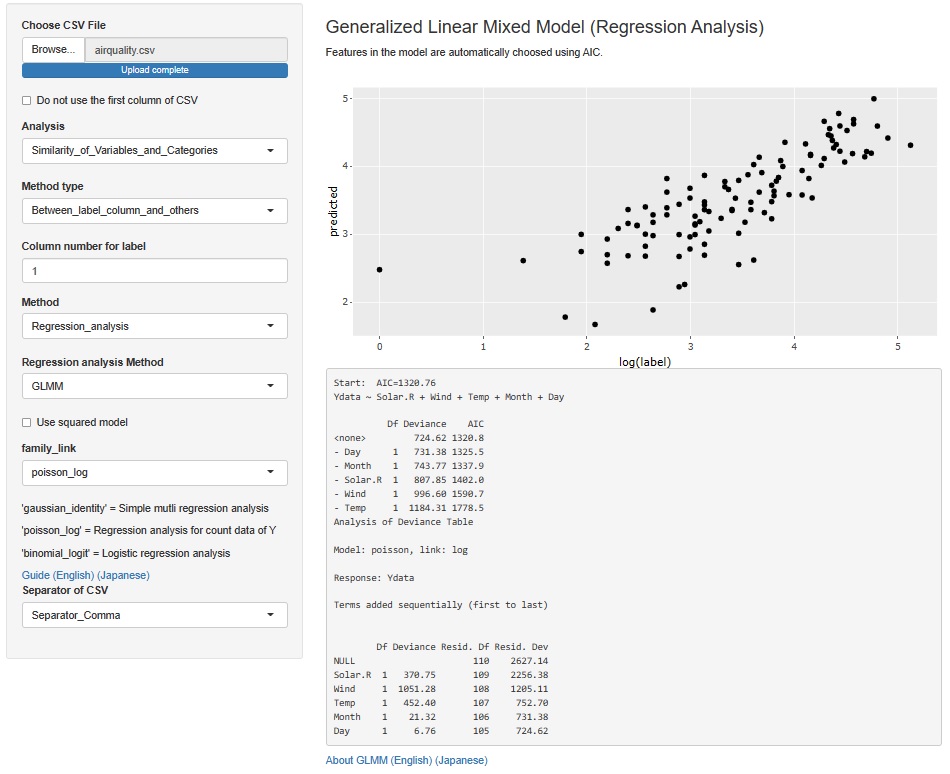
データセットのすべての変数でGLMを実行する機能は、別のところにあります。
「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 久保拓弥 著 岩波書店 2012
この本の著者は、
生態学
の方です。
植物の研究に必要な統計モデリングの理論について、Rを使いながら、順を追って解説しています。
ネットや別の本の中で、この本が
データサイエンス
の教科書のように紹介されているのを見たことがあります。
筆者の推測ですが、その理由は、
データサイエンス
の使い道が
マーケティング・サイエンス
になっている人が世の中に多いことと、
マーケティング・サイエンス
が扱う「人」の研究は、植物の研究と共通点が多いためと思います。
・植物の研究対象になっているデータでは、等分散の仮定が成り立たず、ポアソン分布を仮定した方が良い。
→ ポアソン分布を扱う理論として、GLM（一般化線形モデル）。
→ 現実のデータの個体差を扱うために、GLMM（一般化線形混合モデル）。
→ 複雑になったモデルのパラメータの推定の方法としてMCMC法。
→ 個体の違いがパラメータの違いにも入ることを扱う方法として、 階層ベイズモデル。
→ 位置情報も入れて、空間統計学の理論に。
「空間統計学 ：自然科学から人文・社会科学まで」 瀬谷創・堤盛人 著 朝倉書店 2014
付録で、一般化線形モデルを解説。
空間統計学ではポアソン回帰が多い。
空間統計学
で扱うデータは、隣合ったデータの値が近い、という性質があります。
このため、スプライン関数を使ったモデルがあり、「加法モデル」と呼びます。
加法モデルを実際に解くには、固定効果とランダム効果を使った混合モデルで定式化すると、データへの過剰適合が避けられて良いそうです。
計量経済学でも、「固定効果」、「変量効果」という言葉が出て来ますが、上記のものと意味が違います。
各カテゴリのYの平均値とXの平均値に注目して、平均値の分布を見たときに相関があるものを固定効果と言います。
相関のないものが変量効果（ランダム効果）です。
「計量経済学」 浅野皙・中村二朗 著 有斐閣 2009
ダミー変数を使用しない方法として、各カテゴリで、平均値を計算して、
平均値を引いたデータで回帰分析を行う方法（Within）と、平均値の回帰分析を行う方法（Between）の組み合わせがある。
各カテゴリの平均値に相関がない時が、ランダム効果モデル。
相関がある時が固定効果モデル。
固定効果モデルの時は、全データから作られる傾きと、平均値が作る傾きが一致する。
（この本では、カテゴリ毎に傾きが異なるような状況は、想定されていません。
上記の話は、傾きが一定とみなせる時に有効です。）
「計量経済学」 西山慶彦 他 著 有斐閣 2019
変量効果や固定効果として、重回帰式に項を加えるモデルが出て来ます。
固定効果のモデルには、固定効果としてひとつの項を置くものと、ダミー変数を使って複数の項を置くものがあるが、
説明変数に掛け合わせる係数は両者で同じになる。
固定効果と変量効果を見分ける方法にハウスマン検定があるが、使い方が難しい。
ミクロデータの分析として、
重回帰分析
の仲間の方法を紹介し、マクロデータの分析として、
自己相関分析
の仲間の方法を紹介。
「計量経済学の第一歩」 田中隆一 著 有斐閣 2015
説明変数にダミー変数を入れて、カテゴリ毎の切片を変えたり、ダミー変数と説明変数の交差項を入れて、カテゴリ毎の傾きを変える方法を
紹介。
グループ間の違いの検定としては、チョウ検定（Chow）がある。
固定効果モデルの場合は、一括したデータを使って回帰分析をしても良いが、変量効果モデルの場合は、別の方法がある。
順路
次は
区間高次元化回帰分析
Tweet
