です。このような式は、 線形和 といいます。
Yが１個で、Xが複数の場合の 回帰分析 は、重回帰分析と言います。
重回帰分析の一番簡単な式の形は、
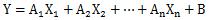
です。このような式は、
線形和
といいます。
より良いモデルの作成には、Xの２乗以上の項を入れたり、 異なるX同士の積を入れることもできます。
目的変数の実測値（元のデータの値）と、予測値（回帰式から求まる値）の 相関係数（決定係数） で、回帰式の良さを評価できます。 例えば、完璧に予測できる式が作れれば、1になります。
相関係数の２乗は、決定係数と呼ばれます。 また、決定係数には寄与率として使える性質があります。
例えば、この値が0.8になったら、「回帰式で、80%予測できる」という言い方ができます。 ちなみに、会議などで、この言い方を使って分析結果を説明すると、重回帰分析を知らない人でも感覚的に理解しやすくなり、 分析結果の後の対策について、同意をしてもらいやすくなります。
なお、式の当てはまりが悪くても、Xの数が多いほど過学習しやすくなり、決定係数の数字が大きくなる現象が起きるため、 単純に大きければ良いと言う尺度ではありません。
この欠点の補正として、調整済み寄与率や、AICと言った尺度が考え出されていて、標準的に出力するソフトもあります。
重回帰分析では、複数の説明変数を使いますが、すべての変数が同じくらいの重要というケースは、あまりありません。 回帰式の精度に強く影響している変数があれば、まったく影響していない変数もあります。
重要度の違いがわかると、 定量的な仮説の探索 ができるようになりますし、下記の「変数の選択」もできるようになります。
重回帰分析では、係数（偏回帰係数） Ai の大きさで、 その説明変数の影響力を比べたくなります。
しかし、一般的には、係数は単位が異なりますので、 次元解析 の観点からも、不用意にはできません。 比較をするには 標準化 を行っておく必要があります。 統計ソフトによっては、標準偏回帰係数も計算されますので、これを使うのでも良いです。
また、係数の比較が純粋に適用できるのは、説明変数同士が無相関（独立）の場合です。 説明変数同士に相関がある場合は、 係数にその影響が含まれていることに注意しなければいけません。
ちなみに、偏回帰係数と、 偏相関係数 は、名前が似ていますが、別物です。
ソフトによっては、変数毎の分散比、t値、p値が表示されることがあり、これらでも変数の重要度が評価できます。
係数の評価は、回帰式の中の、変数の重要度の分析をする方法です。
ところで、 定量的な仮説の探索 の目的は、データセットの中の、変数の重要度の分析です。
係数の評価は、両方に対して使えます。 後者だけに使える方法については、 「変数の重要度の分析」のページにまとめました。
重回帰分析では、Xが複数のため、Xの扱い方や考え方が必要になって来ます。 この辺りの考え方は、重回帰分析だけではなく、 多変量解析 や、 データマイニング 等、多変量を扱う手法で共通です。
重回帰分析では、すべてのXの項目を使って式を作るよりも、 項目を選んだ方が役に立つ式になることが多いです。 例えば、 因果推論 をする時には、多くても3つ程度までにした方が良いです。 そうしないと、因果関係の考察が困難になります。 筆者の経験の範囲では、3つ以上の変数（現象）が絡んでいる場合は、 そもそも重回帰式で表現する事にも無理があったりします。
統計ソフトによっては、すべてのXの項目を使って式を作る機能しかないものもありますが、 手動や自動でXの項目を選ぶ機能が付いているソフトもあります。
変数の選択の方法の種類については、 変数の選択 のページにまとめてみました。
変数の選択をしないと、 変数の重要度の過少評価 をしてしまうことがあります。
順路
次は
単回帰分析の結果と同じ時と違う時
