単回帰分析

Yが1個、Xが1個の回帰分析は、単回帰分析と呼ばれます。 Xが複数になると、重回帰分析と呼ばれ、計算で気を付けることが増えます。

式の形

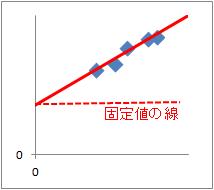
回帰分析では、XとYのデータが、
Y = A * X + B
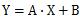
の式で表せると仮定した場合に、どのくらいこの式に当てはまるのかや、AやBの数字（係数）がいくつになるのかを調べる事ができます。

式の係数を求めると、式が完成します。係数の求め方の代表的なものが、最小二乗法です。その他に、最尤法もあります。

この方法を使うと、持っているデータに対して、もっともらしいAやBの値が求まります。

式の妥当性や有効性は、相関係数や寄与率で評価します。

相関係数によって、YとXの値の増減の仕方が似ているかどうかを調べることができます。

相関係数の考え方は重要ですが、少々ややこしいです。詳しくは相関性のページです。

求めた式のもっともらしさは、寄与率で判定します。寄与率は、決定係数とも呼ばれます。

「寄与率」の名前にも出ていますが、寄与率は、「目的変数の変動を、回帰式で説明できる割合」なので、回帰式の説明能力の指標として使われます。寄与率が高くないと、回帰式を予測に使ったり、傾きや切片の数字を現状を表す数値として使ったりできません。

下の図は、XとYのグラフと、XとEのグラフです。 Eというのは、Yから回帰式の分を差し引いた値です。寄与率がR2ですが、R2の0.832というのは、Y全体のばらつきの内、回帰式の直線の分の割合を示しています。その残りのばらつきが、Eのばらつきになっています。
correlation

ちなみに、相関係数を二乗しても、寄与率を求める事ができます。

寄与率は、相関関係の探索で重要な尺度になります。

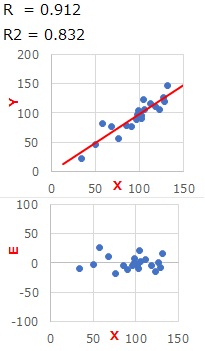
上の式で、Aは傾き、Bは切片と呼ばれます。

上の式で、A・Xの部分は、Xの大きさによって変わる部分（変動分）です。 Bの部分はXがいくつになっても一定（固定分）です。

そこで、Aを変動分、Bを固定分の現状を表す尺度として使う事ができます。２つに分かれると、変動の理由が考えやすくなり、対策も立てやすくなります。

Xを生産量、Yをコストにすると、固定費と変動費のコスト分析ができます。また、 Xを生産量、Yを使用エネルギーにすると、省エネのための分析で使う事ができます。

コストの分析や、エネルギーの分析でしたら、固定分を減らす事と、傾きを小さくする事が対策のヒントになります。

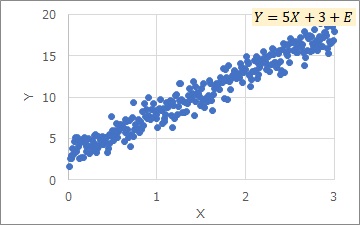
一般的な単回帰分析が使う式は、下記のようなものです。
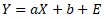
proportional regression

これがぴったり当てはまる分布は、下のグラフのような分布です。 aが傾き、bがY切片、と呼ばれています。 Eというのは、ばらつきです。このモデルでは、縦方向のばらつき方が一定です。
proportional regression

E = Y - 5X - 3
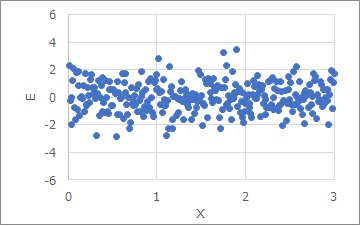
とすると、Eが求まります。 Eは、残差と呼ばれます。

残差Eをグラフにすると、下図になります。 Xがいくつになっても、Eのばらつき方は同じくらいです。これは「等分散」と呼ばれています。
proportional regression

このサイトでは、非等分散の回帰分析のページがあります。

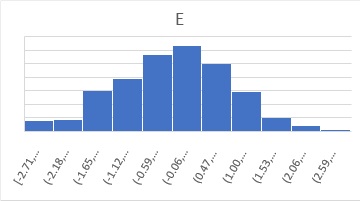
残差Eのもうひとつの特徴として、正規分布があります。一般的な回帰分析では、残差Eが等分散なだけでなく、それが正規分布をしていることを前提にしています。例えば、上記のEのヒストグラムは、下図になっていて、正規分布になっています。
proportional regression

残差に正規分布以外も扱う話は、一般化線形モデルのページがあります。