、と言った式を使います。 Yを結果と考えられる変数にして、Ｘを原因と考えられる変数にしていきます。
相関関係と因果関係 の考察の前に、相関関係がどこにあるのかわからないことがあります。 このページは、相関関係の見つけ方です。
たくさんある変数から相関関係の高い変数の組み合わせを探す作業は、 「スクリーニング（選別）」と言います。
スクリーニングには、 多変量解析 や データマイニング の手法の中にあるモデルを使います。
例えば、
重回帰分析
でしたら、
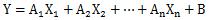
、と言った式を使います。
Yを結果と考えられる変数にして、Ｘを原因と考えられる変数にしていきます。
予測モデルを作る時は、モデルに使う変数を限定して行きますが、 スクリーニングでは、統計モデルだけで注目する変数を限定しない方が良いです。 機械的に 変数の選択 の方法を使うと、因果関係とは無関係でも、様々な理由で相関が高くなっている変数が選ばれますので、 p値 の一番小さい変数が、原因に一番近い変数とは限りません。 「p値が小さい順にした時の、上位1割の変数」や「p値が0.001以下」といった基準にして、 複数選んでおくと良いです。
いくつかの統計モデルを使って、こうした作業を進めると、自分の扱っているデータの特徴に、改めて気付くことがあります。 そして、この気付きが、原因の解明に役立つことがあります。
スクリーニングした変数とYについて、散布図で分布を見たり、 折れ線グラフ を使って時系列の変化を見ます。 スクリーニングしていると、ひとつずつの関係を丁寧に吟味することができます。 そうすると、「今回は、たまたま相関関係が高くなったみたいだな。」、 といった感じで、さらに変数を絞り込むことができます。
こうしてデータを丁寧に見ていく時にも、自分の扱っているデータの特徴に、改めて気付くことがあります。 この気付きも、因果関係の解明に役立つことがあります。
結果になる変数がひとつあって、原因と考えられる変数がたくさんあるような場合、 Yが量的変数の時は 重回帰分析 、 Yが質的変数の時は パターン認識 （ 判別分析 など）を使うと、スマートな解析になります。
しかし、何かの結果が、他の何かの原因になっていたりして、結果系と原因系に変数を分けられない事もあります。
そういった場合は、 多変量データの相関分析 、 ベイジアンネットワークによるデータの構造解析 、 アソシエーション分析 が使えます。
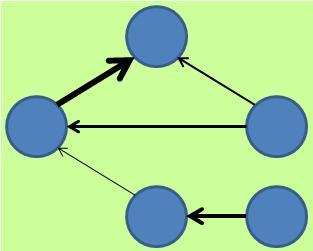
ベイジアンネットワーク は因果関係の分析に使われます。 ベイジアンネットワークによるデータの構造解析 によって、因果関係を自動的に見つける研究もありますが、基本的には ベイズ統計 のページにもあるように、どれが原因でどれが結果かは、人が指定して使うものです。
また、 有向グラフになるデータの構造 がいくつかありますが、 データ構造から導かれる矢印と、因果関係の向きは異なります。 if-thenルールになるデータの構造 には、逆向きの場合の例があります。
これらの統計モデルは、結果が矢印を使ったグラフ（有向グラフ）で表される事もあるので、「 連関図 が自動でできる！」と思いたくなりますが、そうでもないです。
「因果関係の探索」では、結果を表す変数をＹとして、 重回帰分析 などの教師ありの統計モデルを使うのがイメージしやすいと思います。 教師ありの統計モデルを使うには、「これが原因系、これが結果系」という風に変数が区別できている必要があります。
何かの結果が他の何かの原因になってい場合など、因果関係が複雑な場合では、 主成分分析 等の、いわゆる教師なしのモデルを使う手もあります。 原因系と結果系の区別をせずに解析してから、原因と結果の考察を進めるアプローチになります。
「グラフィカルモデリング」 宮川雅巳 著 朝倉書店 1997
グラフィカルモデリング
の本ですが、データ解析の目的は因果メカニズムの究明として解説しています。また、因果推論のためのデータ解析の考え方もあります。
解析の目的が仮説探索や構造探索の時は、唯一無二のモデルを選択する必要はなく、モデル選択の過程自体が解析の道具としています。
データだけからは、相関はわかっても因果関係はわからない事については、
固有技術の立場からモデルを作って、そのモデルを検証するアプローチを解説しています。
ただ、そもそもモデルがわからない状況だからこそ、解決策を見つけるためにデータ解析を始めるので、
それが固有技術の知識でモデルを予め作っておくアプローチが広まらない理由と考えています。
「統計的因果推論 回帰分析の新しい枠組み」 宮川雅巳 著 朝倉書店 2004
同著者の「グラフィカルモデリング」よりも、数学的な記述が深くなっています。
また、前著にはほとんどなかった、有向グラフの話にかなりのページを割いています。
因果関係が量的変数の回帰モデルで表現できる場合の本です。
回帰モデルの使い方や有向グラフの使い方などがあります。
「グラフィカルモデルによる統計的因果推論」 宮川雅巳 著 日本統計学会誌 第29巻、第３号 1999
https://dl.ndl.go.jp/view/download/digidepo_10821860_po_ART0003562538.pdf?contentNo=1&alternativeNo=
30ページ近くあり、同著者の上記の本とほぼ同じ内容になっています。
ベイジアンネットワーク関係の文献は ベイジアンネットワークによるデータの構造解析 にあります。
「統計的因果探索」 清水昌平 著 講談社 2017
LiNGAMを中心にしています。
「つくりながら学ぶ！ Pythonによる因果分析 因果推論・因果探索の実践入門」 小川雄太郎 著 マイナビ出版 2020
この本の特徴は、紹介している方法をPythonで実行することができて、著者のGithabから簡単にコピーして使えるようになっているそうです。
また、Pythonの実行環境は、Google Colaboratoryを使っていて、Pythonを自分でのパソコンではなく、無料の外部環境で使う方法を紹介しています。
この本での、「因果推論」とは、原因の違いによる結果の大きさの違いを定量的に計算する方法でした。
バックドアなどの知識を使って計算します。
この本では、この計算をする方法として
重回帰分析
を紹介して、次に、
ランダムフォレスト
を使った非線形な場合も紹介しています。
シンプルな
回帰木
については、ランダムフォレストの説明のために少し出てくるだけで、これを使った定量的な計算は、説明が飛ばされています。
また、この本での、「因果探索」とは、変数間で因果関係の矢印がわからない場合に、この矢印を見つけるための方法でした。
この方法として、
LiNGAM
、
ベイジアンネットワーク
、
ディープラーニング
の３つを紹介しています。
ディープラーニング ： SAMというディープラーニングの一種の方法を使うと、
隣接行列
が求まるそうです。
これを使って、有向グラフを作ることができます。
順路
次は
相関関係がない時の探索
