判別分析

いわゆる「判別分析」は、ラベル分類としては、古典的なものです。

判別分析には、線による判別と、距離による判別の２種類があります。

なお、判別分析はシンプル過ぎて、実務の目的に合わないことが多く、実務で使うことは、少なくとも筆者はないです。しかし、他のラベル分類を使う時に、判別分析の知識があると、とても役立ちます。

線による判別

一般的には、直線で判別します。場合によっては、2次曲線が使われることもありますが、それ以上、複雑な線は、この理論では使われません。
判別分析

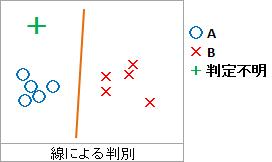
線による判別とは、正確には、Xが2変数の時の話です。

また、Xが3変数の時には、直線ではなく平面、4変数以上だと、超平面が使われますが、やることは「線」の理論と同じですので、ここでは「線」と書いています。

ある線を使えば、その線のどちら側にデータがあるのかで、判別できると仮定します。その線の式は、予測値が0より大きいか小さいかが、2群のどちらかを表すとします。

そうして、その式の係数を計算します。

判別直線を計算する方法として、判別分析は古典的です。比較的新しい方法に、サポートベクターマシンがあります。

判別分析は、全体的な分布がもっとも分かれるような判別直線を見つける方法です。

サポートベクターマシンは、判別直線付近のデータがもっとも分かれるように、判別直線を見つける方法です。「判別を間違えやすいのは、判別直線付近のデータなので、間違いを減らしたいのなら、判別直線付近のデータを重点的に扱った方が良い」、という考え方でできています。

マハラノビスの距離を使って、それぞれの群の中心からの距離を計算し、近い方の仲間と判断します。
判別分析

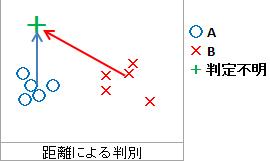
「中心からの距離を見よう」という発想の中に、それぞれの群が正規分布している事が仮定されています。

検定の理論の中で、「5%以下の確率かどうか？」、という話がありますが、正規分布である事を仮定していますので、こういった確率の計算ができます。

ロジスティック回帰分析だと、AとBの確率の合計は、100%になるように計算されます。ところが、距離による判別分析の場合は、2つの群に対しての確率を独立して見るので、「どちらの群の確率も20%以下で、どちらの群でもないかもしれない」、という結果もあり得ます。

線による判別では、必ずどれかのラベルに分類されます。一方、距離による判別では、一番可能性の高いラベルを選べるのは、線による判別と同じなのですが、「どちらのラベルでもないかもしれない」ということも調べることができます。

線による判別では、空間上に線を引くので、ラベルのサンプルが空間上である程度分かれていれば実施できます。一方、距離による判別では、各ラベルが、空間上にそれぞれ塊のようになっている必要があります。こうなっていることで、「どちらでもない」という分析ができます。