「距離」という言葉は、日常的にも使います。 マハラノビスの距離（Mahalanobis' Distance：MD）は、その名前にあるように距離の一種です。
定義式は、下記に詳しく書きましたが、MT法では、一般的なマハラノビス距離を分析に便利なように改良して使います。
一般的なマハラノビス距離については、 ユークリッド距離とマハラノビス距離 のページがあります。
MT法 は、マハラノビス距離を使うものの代表的なものです。 Mは、マハラノビス距離を使っているところから来ています。
例えば、 判別分析 でもマハラノビス距離を使います。
世の中の「マハラノビスの距離」には、いくつかの定義があります。 数学（統計学）関係と、 品質工学 （ MT法 ）関係で異なるので、使う時には注意が必要です。
ここでは、変数が x と y の、2個の場合を例にします。 「 i 」は、「 i 番目のデータ」という意味です。
ユークリッド距離とマハラノビス距離 に計算の手順があります。
定義１だと、下のようになります。
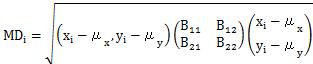
Bの入っている行列は、共分散行列の逆行列です。
MT法
では、定義１の計算式に、変数の数（k）で割る部分が追加されています。
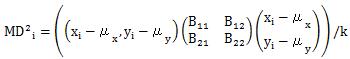
上記は、「マハラノビスの距離の２乗」を計算する式になっていますが、 MT法を使う実務の中では、「マハラノビスの距離の２乗」を「マハラノビスの距離」と省略して呼ぶ事が多いです。
下記にあるマハラノビス距離の２乗の平均値もそうなのですが、 マハラノビスの距離を実際に使ったり、議論する場面では、平方根にする前の、２乗した値の方が見通しの良いデータ分析ができます。
定義３は、MDの数字は定義２と変わらないのですが、データを詳しく分析したい時に便利な方法です。
データを 標準化 してから、定義２の計算をします。
一点注意があり、標準化で使う標準偏差は、分母をnで割った標本標準偏差です。 実務で標準化をする時は、nで割ってもn-1で割っても結論は変わらないことが多いですが、 マハラノビス距離を計算する時は、使い分けを気を付ける必要があります。 平均値の計算が合わなくなったりします。
MT法で計算がおかしい時 にあるように、 マハラノビスの距離の計算をして、うまく行かない理由は大きく分けると２つあります。 定義３で計算を進めると、うまく行かない時に、どちらの理由なのかが見つけやすいです。
まず、各変数の標準偏差を計算しますので、この値を、標準偏差が０の変数、つまり、同じ値しか入っていない変数があるかのチェックに使えて便利です。 このような変数が含まれたままで、マハラノビスの距離を計算しようとするとエラーが出ます。
また、標準化した値で求めた共分散行列は相関行列になり、行列の成分が 相関係数 になっています。 相関行列は、 多重共線性 のチェックに役立ちます。 多重共線性 のある変数の組合せが入っていると、マハラノビスの距離の計算でエラーが出ます。
MT法の手順 にExcelのサンプルファイルがありますが、これは定義３を使っています。
マハラノビス距離の計算では、用意したサンプル全部を使った平均値や分散を使います。 この処理が入っているため、計算された各サンプルのマハラノビス距離の平均値には、特徴があります。 この特徴は、データ分析で活用できます。
定義１の場合、マハラノビスの距離の２乗の平均値は、変数の数とぴったり同じ数値になります。つまり、
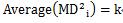
となります。
上記の例でしたら、変数が x と y の２個なので、k は２になります。
定義２・３の場合、kで割る処理が入っているので、変数の数とは関係なく１になります。つまり、
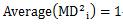
となります。
平均値が、理論上、いくつになるのかがわかっていると、マハラノビスの距離の計算が正しくできているかどうかの確認や、 値を分析する時の指標になります。
実際にマハラノビス距離を使う時には、計算に使う変数の組み合わせを、いろいろと変えて分析することがあります。
定義１の場合は、マハラノビス距離が「2.4」と計算された場合、変数の数が３個だと、「平均値よりも小さい」となり、変数の数が２個だと「平均値よりも大きい」 というように、考察の仕方が変わります。
定義２・３の場合、変数の数に関係なく、マハラノビス距離の２乗の平均値は、必ず１になります。 そのため、変数の数を気にせずに、いつでも１を目安にして考察できるようになります。 MT法による異常の判定 の時に便利です。
マハラノビスの距離の２乗の平均値が、ぴったりとした整数になるのは、不思議な感じがします。
定義２の場合を確認してみることにします。
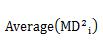
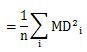
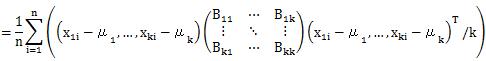
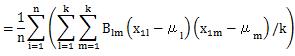
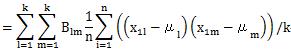
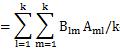
ここで出てきた式は、BとAの積の行列の対角成分と同じ式になります。
BとAの積の行列は、単位行列なので、その対角成分は１です。
これを、次の変形で使います。
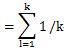
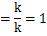
繰り返しになりますが、共分散や標準偏差を計算する時に、分母を「n」にしないと、上記のような式の展開にはなりません。
「タグチメソッドの探究 技術者の疑問に答える100問100答」 宮川雅巳,・永田靖 著 日科技連出版社 2022
MT法で、変数の数で割った値を、マハラノビス距離としているのは、平均を１にすることにより、変数の選択をしやすくしている、という意味の説明がありました。
順路
次は
MT法とホテリング理論の違い
