ベイジアンネットワークによる確率計算 のページは、 個々の現象のネットワークが分かっていて、また、 個々の関係の発生確率のデータを持っていて ベイジアンネットワーク のモデルが作れる場合をスタートにしています。
ところが、実際にベイジアンネットワークを使いたい時には、 ネットワークの構造がわからなかったり、発生確率のデータがない時もあります。
こうした事前情報はないけれども、 多変量解析 で使うような表形式のデータはある時に、 表形式のデータから発生確率のデータを作り、ベイジアンネットワークのモデルを作ってしまう方法が、 このページの話になります。
ベイジアンネットワークの文献の中で、モデルの作成や、因果探索の方法として紹介される方法は、条件付きの確率を調べる方法になっています。
条件付き独立による探索 と スコアによる条件付き確率の探索 に、大きく分かれます。
両方のハイブリッドもあります。
条件付き独立による探索 は、ボトムアップのアプローチです。 一方、 スコアによる条件付き確率の探索 は、トップダウンのアプローチです。 ハイブリッド式は、トップダウンのアプローチの弱点をボトムアップのアプローチで置き換えるものが多いようです。
有向グラフになるデータの構造
には種類がありますが、
条件付き独立による探索
は、
条件付き独立になるデータの構造
を調べる方法です。
一方、
スコアによる条件付き確率の探索
は、
情報量の変化があるデータの構造
を調べる方法です。
ベイジアンネットワークによる構造探索のアルゴリズムの違い や ベイジアンネットワークによる構造探索のノウハウ のページでは、既存のアルゴリズムについて、 EDA（探索的データ分析） を目的とした時の使い勝手を、筆者なりに検証しています。
その観点では、既存のアルゴリズムは、どれも、あまり良くないです。
ハイブリッド有向相関分析 と、 有向情報量分析 は、筆者が考案したアルゴリズムです。 既存のアルゴリズムの弱点に対して、対策した方法です。
まず、サンプル数が多いと、過学習しやすい弱点はなくしています。
また、いずれもボトムアップのアプローチを採用しています。 変数に過不足がある場合は、ボトムアップのアプローチの方が、融通が利きます。
ハイブリッド有向相関分析 は、量的変数用のアルゴリズムです。
既存のアルゴリズムでは、 条件付き独立による探索 と似ていますが、独立性の検定は使わずに、相関係数と偏相関係数を使います。
また、 条件付き独立による探索 では、矢印の方向が決まらない部分については、 正規化による有向相関分析 を活用しています。
有向情報量分析 は、質的変数用のアルゴリズムです。
既存のアルゴリズムでは、 スコアによる条件付き確率の探索 と似ていますが、対数尤度をベースにしたスコアではなく、情報量をベースにしたスコア使います。 「対数尤度」と「情報量」という名前だけだと、だいぶ違うようにも見えますが、 対数尤度と情報量の関係 のページにあるように、両者には関係式があるので、とても似ているものです。
また、 スコアによる条件付き確率の探索 のように様々なモデルをトップダウンで探索するのではなく、 条件付き独立による探索 のように、ボトムアップのアプローチです。
Rによるベイジアンネットワーク のページがあります。
R-EDA1
では、RのbnlearnというライブラリをGUIで使えるようになっています。
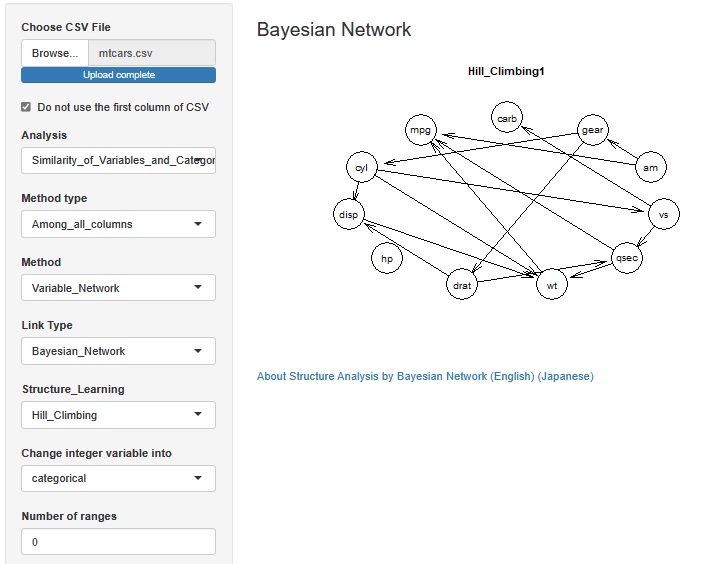
上記の例は、 Hill_Climbingで作っています。アルゴリズムが変わると、矢印の向きが逆になることもあります。
「Change integer variable into」を、 「numeric」にすると、「integer（正の整数）」になっている変数は、量的変数として扱います。 「categorical」にすると、質的変数として扱います。 数字のデータでも、数字の内容が使われないです。 この機能は、integerになっている変数の数字は、その数字が表している数字の大きさに特に意味がない場合がある場合や、 integerになっている変数は、原因側の変数として扱った方が良いことがあるために付けています。 ベイジアンネットワークでは、質的変数と量的変数があった場合には、質的変数から量的変数側に矢印を引くようになっています。
「Number of ranges」が、 例えば、「5」にすると、それぞれの量的変数について、最大値と最小値の間を５個の範囲に均等に分割して、 それぞれの範囲の範囲の名前をカテゴリとする質的変数に変換されます。 １以下の場合は、変換をしません。
Wekaでは、
起動直後のページ → エクスプローラー → 前処理でデータの読み込み、
→ Classifyのタブ → Chooseボタンを押して、小さな選択画面を出す
→ classifiers（分類） → bayes → BayesNetを選択後、Closeで選択画面を閉じる
→ Chooseボタンの右側に「BayesNet」で始まる文字列が出ているので、この文字列の辺りをダブルクリックして、選択画面を出す。
→ serchAlgorithmの右のChooseを押してHillClimberを選択
→ serchAlgorithmのChooseボタンの右側に「HillClimber」で始まる文字列が出ているので、この文字列の辺りをダブルクリックして、選択画面を出す。
→ maxNrOfParentsを変える。（1だと、ナイーブベイズモデルです。
ネットワークっぽくするには、2以上が良いです。
→ 「OK」で選択画面をそれぞれ閉じる。
→ Startで計算
→ Startボタンの下のResult listの中に計算の名前が出ているので、その文字列を右クリック
→ Visualize Graphと進むと、グラフが描けます。
詳しい内容は、シナジーマーケティング株式会社様のブログにもあります。 （ダブルクリックで小窓を出すところが、このブログではわからなかったので、上記で書きました。） http://lab.synergy-marketing.co.jp/blog/statistic/weka-bayesnet2
Wekaの場合は、質的変数が最低ひとつ必要です。 上記のHillClimberの場合は、一番元の親ノードは、解析者が指定する必要があります。また、そのノードは質的変数にしておく必要があります。
「つくりながら学ぶ！ Pythonによる因果分析 因果推論・因果探索の実践入門」 小川雄太郎 著 マイナビ出版 2020
スコアリングによる方法、条件付き独立性検定による方法、ハイブリッド型について、簡単な例が紹介されています。
「Rと事例で学ぶベイジアンネットワーク 原著第2版」 Marco Scutari ・Jean-Baptiste Denis 著 共立出版 2022
構造学習だけで１冊の本になっていて、離散型データの場合、連続型データの場合、混合型の場合、時系列データの場合と続きます。
例題のデータのRによる分析方法を示しながらになっています。
連続型データでは、３変数の間の矢印の有無は、線形の関係、ガウシアン（正規分布）を仮定して、条件付き独立性の検定で判断します。
時系列データの場合は、同一の変数を測定時間ごとに分割して、複数の変数として扱うことで、時系列を扱えるようにしています。
ベイジアンネットワークと
ベイズ統計
の違いについての説明もあります。
「ベイジアンの文脈であるか否かに限らず、データセットからベイジアンネットワークを学習することができる」
制約ベース、スコアベース、ハイブリッドの３種類の大分類について、それぞれの分類の中での、さらに細かな手法の違いについても、解説しています。
「データマイニング入門 ：Rで学ぶ最新データ解析」 豊田秀樹 編著 東京図書 2008
データマイニング
全般の本です。
第7章がベイジアンネットワークです。
データの構造を調べる方法について、Rでの実施例がコード付きであります。
「フリーソフトではじめる機械学習入門」 荒木雅弘 著 森北出版 2014
機械学習全般の本ですが、
Wekaでデータの構造を調べる方法としてベイジアンネットワークを使う例が、少しあります。
「ベイジアンネットワーク」 植野真臣 著 コロナ社 2013
モデルが複雑な時の計算方法、データから発見的にモデルを作るための理論の話が詳しいです。
「グラフィカルモデル」 渡辺有祐 著 講談社 2016
グラフィカルモデルには、２種類あり、ベイジアンネットワーク（有向）と、マルコフ確率場（無向）。
マルコフ確率場は、確率的な依存関係のモデルで例として、統計力学などで出て来るイジングモデルが紹介されていました。
この本全体としては、ベイジアンネットワークの構造の推定の話が多かったです。
隠れ変数のあるモデルの扱い方として、
EMアルゴリズム
がありました。
「条件付き独立性検定による構造学習」 植野真臣 著 2016
http://www.ai.lab.uec.ac.jp/wp-content/uploads/2016/03/7b5a6437c76dc79ac91cbc88217dc84b.pdf
代表的なアルゴリズムが、コンパクトにまとまっています。
順路
次は
ベイジアンネットワークによる構造探索のアルゴリズムの違い
