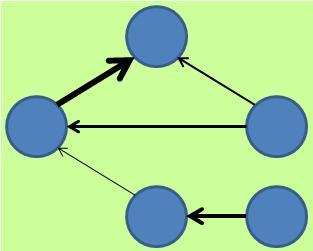
変数間に何らかの非対称な構造がある時に、それを表現する方法として矢印があります。 このようにして作ったグラフは、「有向グラフ」と呼ばれます。
有向グラフは、
定量的な仮説の探索
では、とても魅力的な方法です。
連関図 のようにして、因果関係を表すようにして作る有向グラフと、データの非対称な構造から作った有向グラフは、いずれも矢印を使います。
見た目が同じになっていますし、それらしい理屈を付けることができることもあるので、 データの構造から作った有向グラフは、そのまま因果関係を表すように思えて来ます。 実際のところ、データの非対称な構造から有向グラフができると、それをそのまま「因果関係のグラフ」と説明したり、 少し控えめに、「因果関係の仮説のグラフ」のようにして説明している記事は、とても多いです。
しかし、このようにしてうまく行くのは、以下の場合だけです。 かなり注意深く考察しないと、「因果関係を表している」という解釈はできないです。
if-thenルールになるデータの構造 がわかりやすいと思いますが、 矢印の始点は、原因になる時も、結果になる時もあります。
矢印の向きが因果の向きを表していないことを念頭に置いて、 あくまで、データの非対称な構造を表すグラフとして扱い、その非対称な構造から、データの背景を考察して、因果関係の仮説を考える使い方になってきます。
データの構造から作った有向グラフは、どうやって作ったのかを知らない人が見ると、因果関係を表す図として見られてしまうことが多いです。
そのため、会社の会議や報告書など、いろいろな人が見る資料に、データの構造から作った有向グラフを出すと、混乱の原因になります。 筆者の場合、報告した相手に、「データ分析は、でたらめだ」と、不信感を抱かせてしまったこともあります。
データの非対称な構造は、分野によって、注目されている構造が違っています。 計量経済学 では、 回帰モデルになるデータの構造 を想定することが多いです。 統計的因果推論 では、 回帰モデルになるデータの構造 と 条件付き独立になるデータの構造 を想定することが多いです。
一方、実務の中、例えば、工場の中で起きた問題に対して、因果関係を調べる場合、構造の種類はケースバイケースですし、 複数が混ざっていることもあります。
筆者の経験した中では、データの非対称な構造は、７種類あるようです。 構造の種類をたくさん知っていれば、問題が解決するというものではないですし、データに非対称性のない因果関係もありますが、たくさん知っているに越したことはないと思います。
「結果は原因の後」というのは常識と思いますが、 因果の時間差 以外では、データの表に時刻が含まれていたり、表の順番が時系列になっていても、その情報は使いません。
その意味で、 因果の時間差 は別格です。 データの扱い方が、かなり違います。
順路
次は
if-thenルールになるデータの構造
Tweet
