比例分散モデルになるデータの構造

比例分散の数理モデルの一番簡単な形は、
Y = E * X
という式です。

その次に簡単な形は、
Y = (a + E) * X
という式です。

この式の意味は、「原因であるXと誤差の積が、Yになっている」というものです。世の中で、相関が高いYとXを散布図にすると、Xが大きければ大きいほど、Y方向のばらつきが大きいことがあります。

この構造がわかれば、有向グラフになるデータの構造のひとつになります。
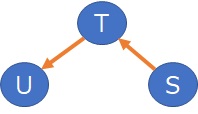
proportional regression

有向比例分散分析を使うと、そのデータにとって、もっともらしい比例分散の関係を見つけられることがあります。