比例分散は、上のグラフのような分布です。 Xが大きければ大きいほど、Y方向のばらつきが大きくなっています。
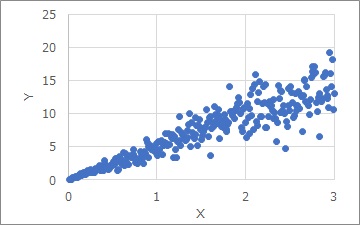
比例分散は、上のグラフのような分布です。
Xが大きければ大きいほど、Y方向のばらつきが大きくなっています。
規模が大きければ大きいほど、ばらつきが大きい場合、このような分布になることがあります。 測定器のデータでも、このような分布になることがあります。
一般的に「比例」と言えば、Xが大きければ大きいほどYが大きくなる関係で、
Y = a * X
という式で表せます。
「比例分散」は、XとYが比例しているだけではなく、Y方向のばらつきもXに比例しています。
なお、「比例分散」というのは、筆者が付けた名前です。 世の中に名前がないようなので、付けたのですが、あればそちらに合わせるつもりです。
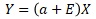
比例分散は、上のような式で表されます。
aが傾き、Eというのは、ばらつきです。
EとXがかけ合わさることで、Xが大きければ、Y方向のばらつきが大きくなることが表現されます。
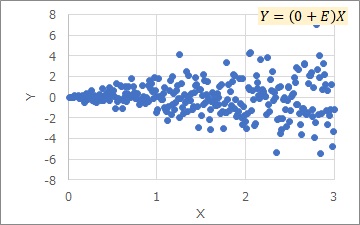
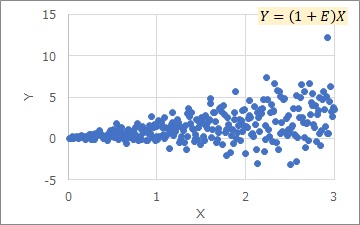
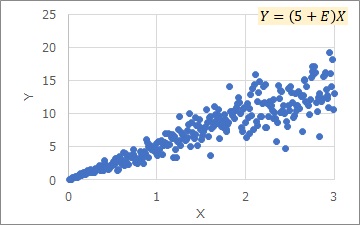
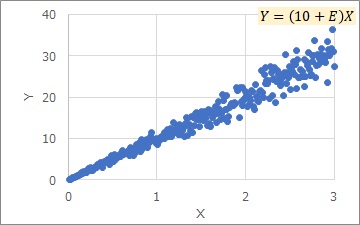
ここでは、Eは一定にしています。aによって、見た目はだいぶ変わります。
比例分散は、比例していることに注目した分類なので、Eの分布に特定の形はありません。 実務で多いのは、正規分布で、次が一様分布かと思います。
「比例分散とは何か？」という点を考察してみました。
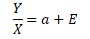
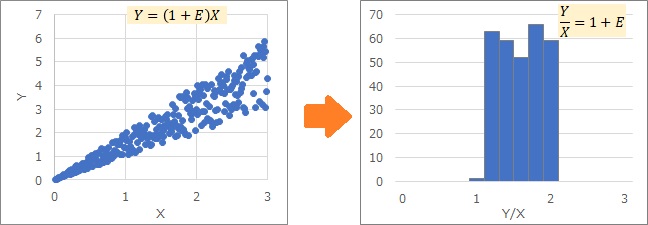
比例分散は、両辺をXで割ると、上記のようになります。
この式の意味は、Y/Xという変数は、中心がaで、ばらつきがEということを表します。
例えば、「Y/Xが正規分布になっている」ということと、この意味は同じです。 統計学で、確率分布と呼ばれているものは、例えば、「Zが正規分布になっている」という見方をしますが、 比例分散の場合は、Zの部分が、Y/Xという２つの変数でできています。
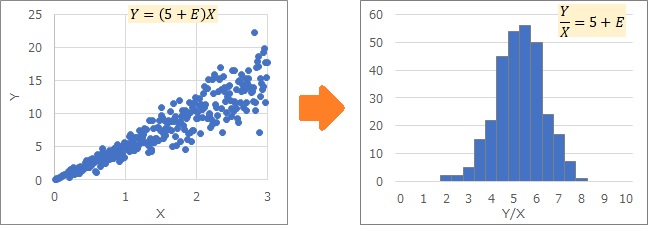
下の２つの例は、いずれも右側がY/Xという変数のヒストグラムです。
比例分散を変形すると、正規分布や一様分布になる様子がわかります。
100m走のコースを作る時には、学校の体力測定のような用途なら、0.3mくらいの誤差ならOKとするのが一般的ではないかと思います。 また、1000m走のコースを作る時には、3mくらいの誤差ならOKとするのが一般的ではないかと思います。
このように、一般的には、基準とする値が大きくなると、許容されるばらつきも大きくなります。 比例分散は、そのような性質を表す数理としても使えるようです。
大きな物を動かすには、大きなエネルギーが必要になります。 大きな物を動かすと、慣性力も大きいので、位置決めがしにくくなります。
このような性質を表す数理としても、比例分散は使えるようです。
実際、 比例分散への品質工学のアプローチ にあるように、品質の分野では比例分散はよく出て来るので、昔から扱い方が研究されています。
比例分散のEは、任意の分布が使えます。
このページのグラフは、EXCELの下記の関数で作っています。
aは傾き、Eは標準偏差です。
a、E、Xのところに値を入れると、Yが求まります。
=NORMINV(RAND(),a * X, E * X)
または
= X * NORMINV(RAND(),a, E)
一様分布の場合、Eはばらつきの範囲（最大値と最小値の差）になります。
= X * (a + E * RAND())
比例分散は、応用がいくつかあります。
順路
次は
質的変数の分布
