比例分散は、上のグラフのような分布です。 Xが大きければ大きいほど、Y方向のばらつきが大きくなっています。
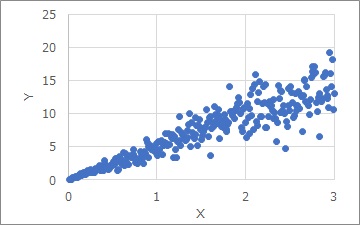
比例分散は、上のグラフのような分布です。
Xが大きければ大きいほど、Y方向のばらつきが大きくなっています。
比例分散の回帰分析は、回帰分析としてはポピュラーではないです。 そのあたりの話は、 非等分散の回帰分析 のページにあります。
以下は、必要に迫られて、筆者が自分で整理した内容になっています。 数学的には、等分散の回帰分析よりも簡単です。 簡単なので、わざわざ説明する人がいないのかもしれませんが、ここでは順を追って説明することにしています。
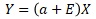
比例分散は、上のような式で表されます。
aが傾き、Eというのは、ばらつきです。
データがある時に、この式の具体的な係数を求める方法が下記になります。
比例分散は、新しい変数を作ると、取り扱いが簡単になります。
下のグラフは、左側がYとXの散布図です。
右側がY/Xと、Ｘの散布図です。
右側のグラフの右上にある式は、左側のグラフの式の両辺をXで割ったものです。
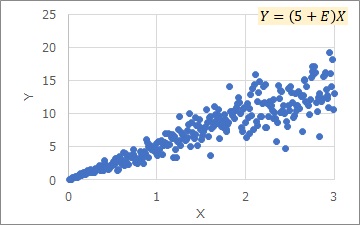
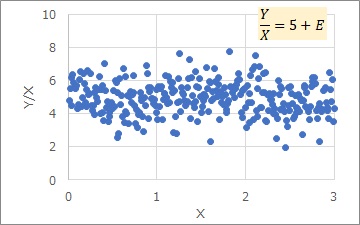
右側は、「Xに関係なく、縦軸のばらつきは一定」ということを表しています。
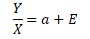
この式の右辺は、「ある値aがあって、そこにばらつきが加わったもの」というです。
正規分布の場合は、分布の平均値がaで、標準偏差がEだと、ちょうどこれに相当します。
つまり、Y/Xという変数は、普通の正規分布で表せるということになります。
「比例分散は、正規分布から作られる分布の一種」とも言えます。
グラフの見た目だけで、aとEの大きさを見積もろうとした場合、変形前のグラフは、aについては「傾きはこのくらいだから・・・」と考えて計算できなくもないのですが、Eの方は、ちょっと大変です。
変形後のグラフの場合、まず、Y方向のばらつきの中心がだいたい5なので、「aは5」と見積もれます。 Eについては、5を中心としたばらつきとして考えると、だいたい1なので、「Eは1」と見積もれます。
比例分散は、一見すると、扱いにくいものですが、ちょっと変形しただけで、普通の正規分布として扱えるようになります。 このシンプルさは、現象の理解にとても強力です。
まず、Eが正規分布の場合です。
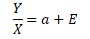
の式により、
a = average(Y/X)
E = stdev(Y/X)
になります。
実際に求める時は、まず、データのYとXを使って、Y/Xという変数を作ります。 この変数の平均値と標準偏差が求めたい係数になります。
Eが一様分布の場合、Eの計算式が違います。
E = max(Y/X) - min(Y/X)
または、
E = sqrt(12)*stdev(Y/X)
です。sqrt(12)というのは、一様分布における、範囲と標準偏差の関係式にある値です。
比例分散をしているデータに対して、普通の 単回帰分析 をする方法としては、以下の２通りが考えられます。 世の中では、この２通りのいずれかで進められていることが、一般的ではないかと思います。
データが少ないと、比例分散であることはわかりにくいので、比例分散に従っているような現象でも、普通の回帰分析で進めて、 特に問題が起きないと思います。
ただ、上記のように、Y/Xを計算して、比例分散として分析すると、残差が正規分布や一様分布になっていることがわかるのに対して、 YとXがそのままの回帰分析では、残差が何かの分布になっていることは、比例の影響でわからなくなっています。
直線の傾きがわかり、そこからのばらつきをグラフで見ているだけなら、このアプローチでも良いですが、ばらつきの評価や分析をしたい場合、 このアプローチは不便です。
下のグラフは、左側が変形前で、右側が両辺とも対数軸（両対数グラフ）にしたものです。対数への変換は、 特徴量エンジニアリング の一種として、よく知られています。
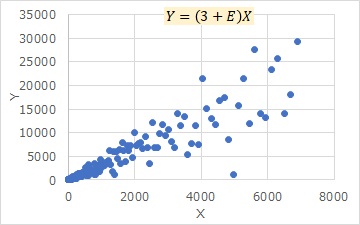
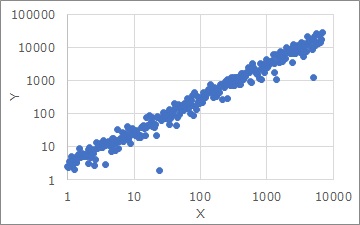
対数にすると、プロットがほぼ一直線に並びますし、Y方向のばらつきも一定のように見えます。
等分散と比例分散 のページに詳しく書いていますが、対数に変換されたデータは、傾きが必ず１になりますし、Y切片も、なぜ、その値になるのかがわかりにくいです。
そのため、このアプローチは、あまり良くないです。
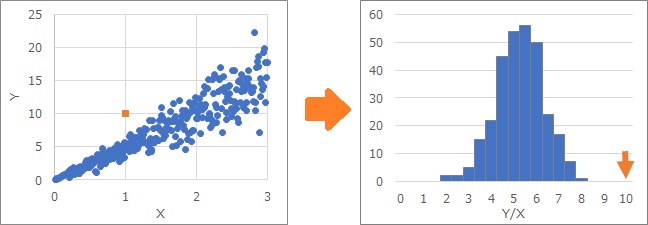
例えば、オレンジ色のようなプロットがあったとします。
Y/Xを計算して、Y/Xのヒストグラムの中で、オレンジのプロットの位置を見ると、外れていることが、シンプルに表現できます。
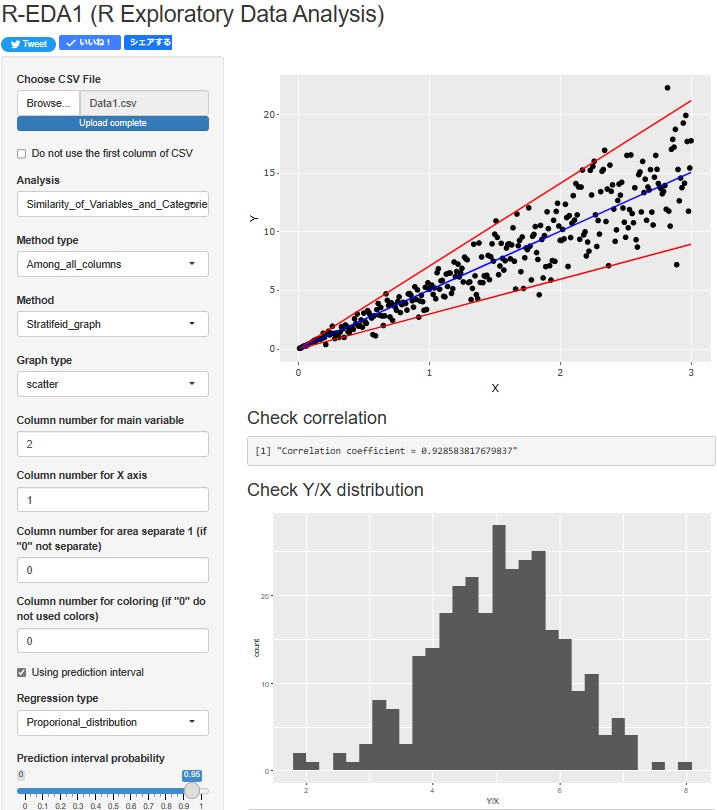
ウェブアプリR-EDA1
でも、比例分散は分析できるようになっています。
順路
次は
非等分散の回帰分析
