トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

比例分散の線形混合モデル

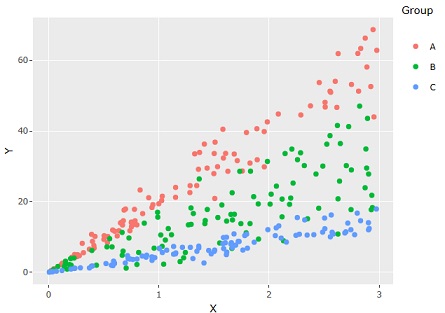
このページは、上のようなデータの話です。 ３つのグループがあって、０から広がっているのは同じですが、広がり方が違っています。

線形混合モデルによる分析

線形混合モデルの見方をすると、「グループで傾きが異なる」という点を考慮して、モデルを作ることができます。

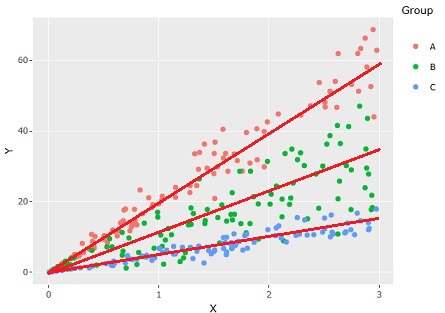
線形混合モデルの場合は、等分散が仮定されているので、 「Xが大きければ大きいほど、Y方向のばらつきが大きい」という特徴には合っていません。 傾きの違いだけに注目したいのなら、線形混合モデルでも良いのですが、ばらつきの分析ができません。

ヒストグラムによる分析

Yだけをヒストグラムにすると、Y方向の広がりが異なることがわかります。

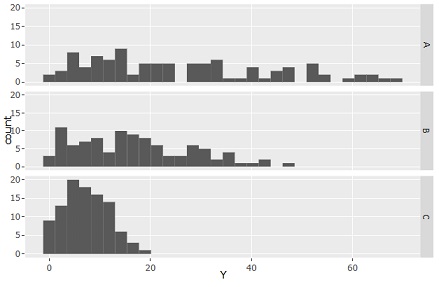
ばらつきの違いの分析はできますが、 「Xが大きければ大きいほど、Y方向のばらつきが大きい」は見えなくなっています。

データの背後に比例分散がある場合、Yのヒストグラムには、 「Xが大きければ大きいほど、Y方向のばらつきが大きい」という性質と、「傾きが大きいと、Y方向のばらつきが大きい」という性質の両方が含まれます。 そのため、傾きが一番大きい、Aのばらつきが一番大きく見えやすくなります。

比例分散として分析

唐突な感じがしますが、Y/Xという変数を作って、これをヒストグラムにします。

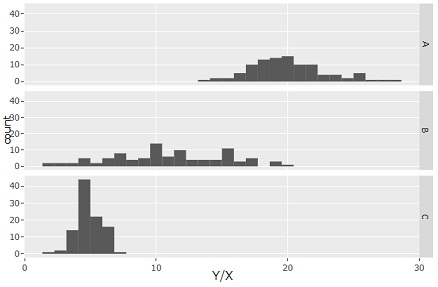
すると、A、B、Cの傾きの違いは、分布の中心の違いで表現できていますし、Bのばらつきが一番大きくて、Cが一番小さい様子も表現できています。 これは、 比例分散の回帰分析 の応用になります。

Y/Xという変数を見るようにすると、傾きの違いと、ばらつきの違いを分離できます。 このため、比例分散のばらつきという観点では、Bのばらつきが一番大きいことがわかります。

グループが多い場合

横軸をY/Xの平均値、縦軸をY/Xの標準偏差にすると、ヒストグラムからわかる情報をシンプルなグラフで表現できます。 この方法は、グループが多い場合に便利です。

比例比例分散モデルの可能性

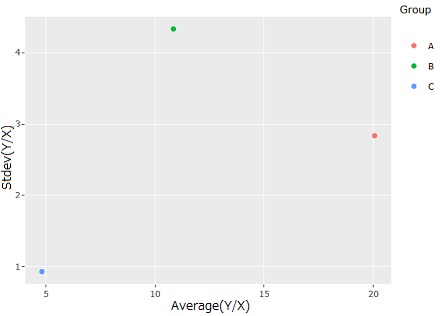
上記の例だと該当しないのですが、Stdev(Y/X)とAverage(Y/X)が一直線に並ぶ場合は、 Stdev(Y/X)がAverage(Y/X)に比例しているということなので、 比例比例分散モデル が当てはまる可能性があります。

順路 次は 比例比例分散モデル