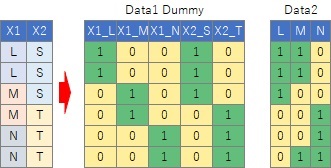
数量化I類は、 数量化理論 の一種です。 オリジナルの数量化Ⅰ類は、 Data1のタイプのデータを説明変数Xとして、 重回帰分析 で分析する方法です。
このページの広義の数量化I類は、
Data2のタイプのデータについても同じように分析することを想定しています。
一番シンプルな例からになります。
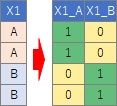
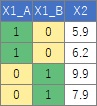
簡単な例として、説明変数がひとつしかなく、「Aさん」、「Bさん」という２つの名前が入った質的データだったとします。
このような場合に、ダミー変換をして、Aさんの時にX=1、Bさんの時にX=0にしたとすると、
数量化I類によって、例えば、
Y = X + 1.3
という式が得られます。
この式は、
Y = 2.3 ・・・Aさんの時
Y = 1.3 ・・・Bさんの時
、という事と意味が同じです。
つまり、質的変数をダミー変数で扱うモデルは、Y切片の分だけずれた場合のモデルです。
言い換えれば、カテゴリ毎に
層別
してY切片を求めています。
説明変数に量的変数と質的変数が混ざっている場合に、質的変数についてはダミー変換をすれば、 重回帰分析をすることができますが、 質的変数が影響するのは、Y切片の部分です。
例えば、AさんとBさんで、Y切片分のずれを考慮するとモデルの当てはまりが良くなる場合には、
この分析は効果的です。
しかし、AさんとBさんの違いによって、式の傾きも変わる場合には、このモデルは良くありません。
傾きが複数あるモデルは、データを加工すると作ることができます。
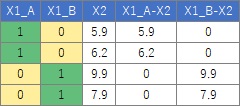
例として、説明変数に、量的変数と質的変数がひとつずつあるとします。
この量的変数と質的変数のダミー変数の積を作り、第３の変数にします。
ちなみに、この変数は「交互作用項」「係数ダミー」と呼ばれています。
上記のようにY切片をずらす時に使うダミー変数は、「定数項ダミー」と呼ばれています。
そして、量的変数、質的変数のダミー変数、第３の変数で、重回帰分析をします。 これが、傾きが複数あるモデルになります。
第３の変数が有意にモデルに影響している場合は、AさんとBさんで傾きが異なることを
検定
したことになります。
また、ダミー変数が有意にモデルに影響している場合は、AさんとBさんでY切片が異なることを検定したことになります。
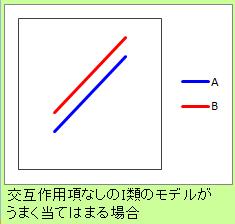
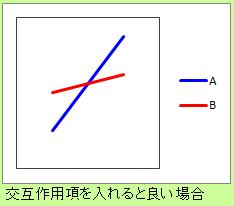
なお、ダミー変数によって、カテゴリ毎に切片や傾きを変えるモデルは、 線形混合モデル と呼ばれています。
「数量化Ⅰ類」という項目が入っているソフトはあまりありませんが、 数量化Ⅰ類は、説明変数を工夫することで実現できるので、回帰分析が入っているソフトがあればできます。
R-EDA1 には、 線形混合モデル の項目があるので、この機能を使って、数量化Ⅰ類ができます。
「データ分析をマスターする12のレッスン」 畑農鋭矢・水落正明 著 有斐閣 2017
計量経済学の分野での
仮説の検証（実証分析）
のためのデータ分析を扱った本です。
ダミー変数を使った
重回帰分析
の話で、ひとつの章になっています。
「図解でわかる回帰分析」 涌井良幸・涌井貞美 著 日本実業出版社 2002
回帰分析を図解でわかりやすく説明しています。
モデルはシンプルな方が良いので、ダミー変数を入れても、決定係数が変わらない場合は、入れない方を採用すべき、としています。
順路
次は
広義の数量化Ⅱ類
