 僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
 僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
僩僢僾儁乕僕 |
傂偲偮忋偺儁乕僕 |
栚師儁乕僕 |
偙偺僒僀僩偵偮偄偰 | ENGLISH
悢検壔嘦椶偼丄 悢検壔棟榑 偺堦庬偱偡丅 僆儕僕僫儖偺悢検壔嘦椶偼丄 Data1偺僞僀僾偺僨乕僞傪愢柧曄悢X偲偟偰丄 敾暿暘愅 偱暘愅偡傞曽朄偱偡丅
偙偺儁乕僕偺峀媊偺悢検壔I椶偼丄
Data2偺僞僀僾偺僨乕僞偵偮偄偰傕摨偠傛偆偵暘愅偡傞偙偲傪憐掕偟偰偄傑偡丅
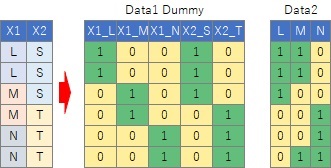
椺偊偽丄壓偺僨乕僞偺応崌丄 僟儈乕曄姺 偡傞偲俁偮偺曄悢偑偱偒傑偡丅 Y傪柧妋偵暘偗傞偙偲偑偱偒傞偺偼乽XS乿側偺偱丄悢検壔嘦椶偼丄偙偆偄偆僇僥僑儕傪尒偮偗傞偙偲偑偱偒傞暘愅曽朄偲尵偊傑偡丅
傾僜僔僄乕僔儑儞暘愅
傗
儔僼廤崌暘愅
偲堘偭偰丄乽X偑S偱偼側偄乿偲偄偆偙偲偲丄Y偑B偱偁傞偙偲偵憡娭偑偁傞偙偲偑尒偮偗傜傟傞偺偑摿挜偲巚偄傑偡丅
偨偩偟丄乽X偑S偱偼側偄乿偲偄偭偨忦審偼丄幚柋偱偺巊偄偙側偟偑擄偟偄傛偆偵巚偭偰偄傑偡丅
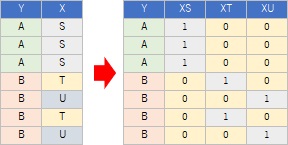
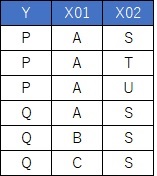
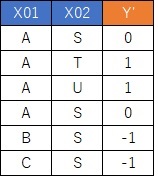
忋偺傛偆側僨乕僞偑偁偭偨偲偟傑偡丅
栚揑曄悢偑Y偱丄愢柧曄悢偑X01偲X02偱偡丅
幙揑曄悢傪曄姺偟傑偡丅
Y偼-1偲1偺2抣偵偟偰丄愢柧曄悢偼僟儈乕曄姺傪偟傑偡丅
X01C偲X02U偑側偄偺偼丄
懡廳嫟慄惈
傪旔偗傞偨傔偱偡丅
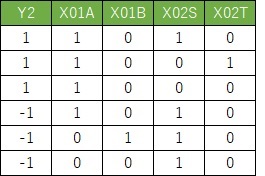
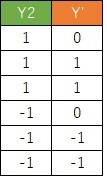
偡傞偲丄梊應抣Y'偑媮傑傝傑偡丅
侽傛傝傕戝偒偗傟偽P偱丄彫偝偗傟偽Q偑懳墳偟傑偡偺偱丄偩偄偨偄崌偭偰偄傑偡丅
侽偪傚偆偳偵側傞僒儞僾儖偼丄偳偪傜偲傕敾抐偱偒傑偣傫丅
侽偪傚偆偳偵側傞僒儞僾儖偲偄偆偺偼丄A偲S偺慻崌偣偺帪偱偡丅
尦偺僨乕僞偱偼丄A偲S偺慻傒崌傢偣偺帪偼丄P偲Q偺椉曽偺応崌偑偁傞偙偲傪丄侽偲偟偰昞尰偟偰偄傞偙偲偑傢偐傝傑偡丅
悢検壔嘦椶偺巊偄摴偲偟偰丄栚揑曄悢傪婎弨偲偟偰丄幙揑曄悢偵側偭偰偄傞愢柧曄悢傪検揑曄悢偵偡傞偙偲偑偱偒傑偡丅
偦偺応崌偼丄
Y'傪乽梊應抣乿偲峫偊傞偺偱偼側偔丄乽栚揑曄悢傪嶲徠偟偰丄愢柧曄悢偺僌儖乕僾傪侾偮偺楢懕曄悢偵曄姺偟偨曄悢乿偲峫偊傑偡丅
弴楬


 師偼
峀媊偺悢検壔嘨椶
師偼
峀媊偺悢検壔嘨椶

