数量化Ⅲ類は、 数量化理論 の一種です。 例として使われるデータの形が異なりますが、 コレスポンデンス分析 と数学的には同じであることが知られています。 コレスポンデンス分析 のページにありますが、 コレスポンデンス分析と 主成分分析 がとても似ているので、数量化Ⅲ類も主成分分析も、とても似ている手法です。
元データが左のような行列データだったとします。
数量化Ⅲ類は、「1」のある部分が対角線上にできるだけ並ぶように、行列を並べ替えます。
すると、XとYの順位データ同士の相関係数が最大化されます。
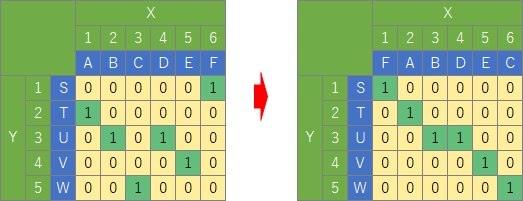
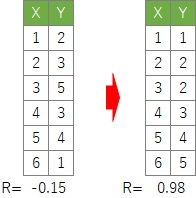
この状態を作った時の、順位データの値が、各カテゴリに何らかの意味のある順番として解釈します。
オリジナルの数量化Ⅲ類では、行と列の並び替えを数学的な手続きで実行します。
なお、上記の説明は、イメージ作りを優先して、正確な表現になっていないです。 上記の例のようなデータだと、並び替えの仕方は様々なパターンがあり、決まらないです。 「1」がもっとたくさん入って来ると、一意に決まってくるようになります。
まず、XとYのそれぞれのカテゴリについて、何らかの意味のある順番がわかるようになります。 この意味で、カテゴリが「数量化」されています。
次に、XとYのそれぞれのカテゴリについての相関の仕方もわかるようになります。
このサイトでは「広義の数量化Ⅲ類」というものを考えてみました。
対象とするデータは、 数量化理論 のページの分け方のData1、2、4になります。
また、
「目的変数なし。カテゴリの座標データを求める分析方法」
と考えています。
オリジナルの数量化Ⅲ類だけではなく、
主成分分析
や
コレスポンデンス分析
も含めたものとしています。
広義の数量化Ⅲ類は、 主成分分析 が中心に書いています。 広義の数量化Ⅲ類となって来ると、質的変数と量的変数の混ざったデータも扱いますが、 コレスポンデンス分析 は、こうしたデータを扱う理論になっていません。
主成分分析は、 変数の類似度の分析 と サンプルの類似度の分析 に使えるものです。
一方で、広義の数量化Ⅲ類は、 カテゴリの類似度の分析 と サンプルの類似度の分析 に使えるものになっています。
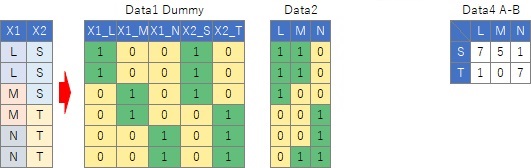
広義の数量化Ⅲ類に主成分分析を使う時に、入力データを作る部分以外は、主成分分析そのものです。 ところが、ダミー変換をしたデータを作ることによって、元々の質的変数について、 変数の類似度の分析 ではなく、 カテゴリの類似度の分析 をするものになっています。
アソシエーション分析 のページでは、質的変数と量的変数の混ざったデータについて、量的変数を質的変数に変換して行った事例を書いています。 量的変数と質的変数が混ざったデータについては、この方法を使ったり 多重対応分析 を使ったりして、「データの構造を見る」というアプローチがベストと、筆者は考えています。
質的変数を ダミー変換 して主成分分析をすることはできるのですが、ダミー変換で作った変数と、量的変数は、相関係数が非常に低くなりがちです。 もともと量的変数だった変数同士の関係と、もともと量的変数だった変数とダミー変換で作った量的変数の関係と、 ダミー変換で作った量的変数同士の３種類の組み合わせについて、別の扱いをしなければいけないのですが、 いったんダミー変換をしてしまうと、別の扱いというのはできないので、変数の関係がうまく評価できなくなります。
そのため、質的変数と量的変数が混ざったデータについては、質的変数の分析手法に持ち込むのがベストと思います。
なお、量的変数がひとつなら、それを目的変数にして、 広義の数量化Ⅰ類 や 回帰木 を使って、データの構造を見る方法もあります。
Data1と4をスタートにする場合は、面白い性質があります。
下の２つのグラフは、同じデータがスタートになっていて、分析方法が違います。
左はデータを分割表にしてから主成分分析をして、主成分得点と因子負荷量を合成したグラフです。
右はデータを
ダミー変換
してから主成分分析をした時の、因子負荷量のグラフです。
左右対称の違いはありますが、ほぼ同じグラフが作られています。
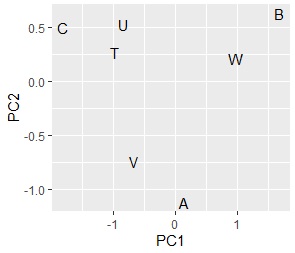
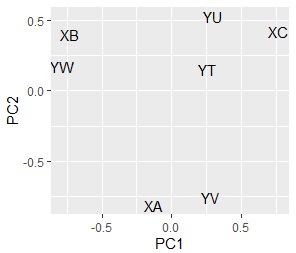
分割表を作るための元データがなくても、元データを分析した時とほぼ同じ結果が出せることから、 元データがなくても、元データがある時と同じような分析ができることがわかります。
分割表を使う方法は、二元分割表を対象にするので、元の質的変数が３個（３列）以上ある時はできません。 ダミー変換を使う方法は、元の質的変数が何個あってもできます。
また、上のグラフでダミー変換を使う方法では、主成分得点の結果は入っていません。 主成分得点の情報から、 サンプルの類似度の分析 もできます。
分割表を使ったり、ダミー変換を使ってから、主成分分析をする方法のRによる実施例は、 Rによる質的変数の主成分分析 のページにあります。
「多変量する解析がわかる」 涌井良幸、涌井貞美 著 技術評論社 2011
0と1だけのデータをスタートにする時の数量化Ⅲ類と、
分割表
のデータをスタートにする
コレスポンデンス分析
は、行列の対角付近の数値が高くなるように行列を変換する点が同じそうです。
「グラフィカルモデリング」 宮川雅巳 著 朝倉書店 1997
「数量化Ⅲ類では、３変数以上の絡みがわからない」として、それがわかる方法として、
グラフィカル対数線形モデル（対数線形分析。生起確率の対数をYにした、交互作用項を含む線形モデル）を紹介しています。
この本は、量的変数のグラフィカルモデリングと、質的変数のグラフィカルモデリングで大半のページを使っていますが、
量的変数と質的変数が混ざったデータのグラフィカルモデリングについても考察があります。
とても難しいテーマで、ひとつの方法は、量的変数は、質的変数に変換して質的変数の方法を使うこととしています。
順路
次は
テキストマイニング
