分割表は、度数を分類して
A-B型
の表にしたものです。
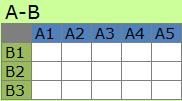
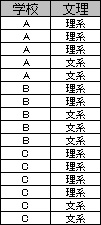
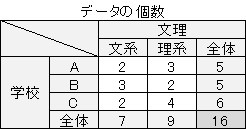
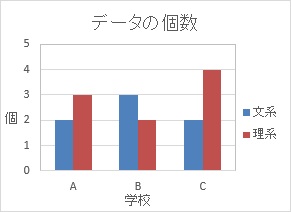
上のデータは、各生徒の学校と文理の分類のデータです。 学校別、文理別でデータの数を数えて集計すると、分割表が作れます。
分割表は、質的データの分析方法として、古くからあります。 分割表を 検定 する方法として、 独立性の検定 というものもあります。
質的変数だけのデータを クロス集計 することで作ることもできます。
上の分割表は、学校と文理という２つの次元で集計しています。 「２元分割表」や「２元表」とも呼ばれます。
少しわかりにくいのですが、２元より多い分割表もあります。
下は３元分割表の例です。
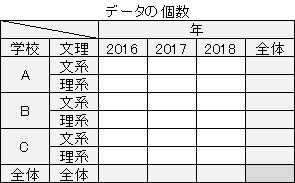
上記のように、質的変数が複数ある場合と、分割表は、見た目が違いますが、同じものと考えることもできます。
対数線形分析 や コレスポンデンス分析 は、どちらの形式からでもスタートできます。
分割表のそれぞれのマスの値には、過去の値や、理想の値、他の地域の値など、比較したい値があることがあります。
こうした値と近いかどうかを判断する 検定 の方法は、「適合度の検定」と言います。
分割表は、 クロス表 の一種です。 ただ、分割表はちょっと特殊で、集計の外側にある数字は、行方向や列方向の合計値です。 クロス表の場合は、必ずしも合計値ではありません。
分割表のこの特徴は、 独立性の検定 の計算の中でも使われます。
２×２の最小サイズの分割表は、 混同行列 として使われ、いろいろな分析方法があります。
Rで分割表を作る時の例は、 Rによるクロス集計 のページにあります。
順路
次は
対応ありの分割表と、対応なしの分割表
