コレスポンデンス分析（対応分析）

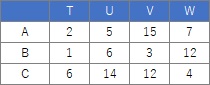
コレスポンデンス分析は、分割表の分析方法として説明されていることが多いですが、質的変数の分析方法としても使えます。
Data Data

ところで、コレスポンデンス分析は数量化Ⅲ類と数学的に同じものであることが知られていますが、数量化Ⅲ類が、分割表の分析方法として説明されることはないです。

また、コレスポンデンス分析は、質的データや計数データを扱う手法として知られていますが、入力データが同じなら、量的変数を扱う手法として知られている主成分分析と、非常に似た結果になります。

コレスポンデンス分析でわかること

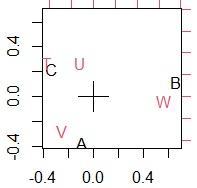
分割表をスタートにする場合は、例えば、「AとVや、CとUは頻度が多いので、関係が強い」ということを、グラフで視覚的に調べる方法になります。

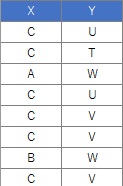
質的変数をスタートにする場合は、カテゴリの類似度の分析になります。わかることは、基本的に分割表の場合と同じですが、質的変数で３変数以上にすると、分割表よりも複雑な関係が調べられます。

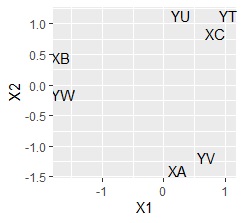
上記の例で、分割表の元データになっているデータは、質的変数が２つ（２列）のデータになります。

分割表の結果と比べる場合は、質的変数が２つのデータと比べることになりますが、コレスポンデンス分析では、質的変数が３つ以上でもできます。この場合は、「多重対応分析」と呼ばれています。

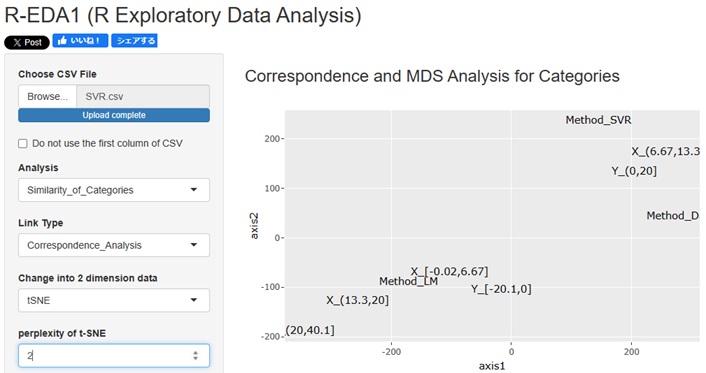
R-EDA1でもできます。
Correspondence analysis

世の中のコレスポンデンス分析の解説は、入力と出力の話が中心で、実際にどのような計算が解説されていないものが、とても多いのですが、以下の文献には書かれていました。

「コレポンは何をやっているのか①数理の概要」　2018
ネット上の数少ない情報源です。
https://yanbow221.hatenablog.com/entry/2018/07/18/212604

「多変量解析がわかる」涌井良幸・涌井貞美　著　技術評論社　2011
一番基本的な計算について、具体的な手順が書かれています。

「多変量データ解析法　理論と応用」柳井晴夫著　朝倉書店　1994
数式を使った説明が詳しいです。
コレスポンデンス分析と正準相関分析の関係についても書かれています。

コレスポンデンス分析の幾何学的意味と導出　北九州市立大学経済学部　齋藤朗宏　著　2017
カイ二乗距離を使う理由が詳しいです。 https://www.kitakyu-u.ac.jp/economy/uploads/2017_04.pdf

「Rによる多変量解析入門 　データ分析の実践と理論」　川端一光・岩間徳兼・鈴木雅之　著　オーム社　2018
「質的変数間の連関を視覚化したい」のツールとして、コレスポンデンス分析が紹介されています。

「すぐわかる　統計処理の選び方」　石村貞夫・石村光資郎著　東京図書　2010
質的変数が３つ以上ある時のコレスポンデンス分析が、「多重対応分析」として紹介されています。

同志社大学　金明哲先生のページ
Rと対応分析 https://www1.doshisha.ac.jp/~mjin/R/Chap_26/26.html