カテゴリの類似度の分析

教師なし学習の手法の使い方に、データの類似度の分析があります。変数の類似度の分析や、サンプルの類似度の分析がよく知られています。

その順番で考えると、カテゴリの類似度の分析は、第３の類似度の分析になります。

カテゴリの類似度の分析とは

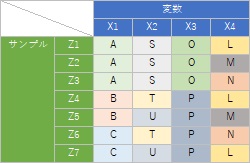
例えば、上のようなデータがあった時に、 X1、X2、等の関係を見るのが、変数の類似度の分析です。 Z1、Z2、等の関係を見るのが、サンプルの類似度の分析です。

カテゴリの類似度の分析では、「AとSとOの組合せには、関係がありそう」といった見方をします。

質的変数だと、このような分析ができます。

変数の類似度の分析は、量的変数の関係を調べるものが多いです。代表的なものが、相関係数による分析です。

質的変数は、ダミー変換で、量的変数に変換できます。

ダミー変換によって作られたデータについて、変数の類似度の分析の方法を使うと、これは、カテゴリの類似度の分析になります。

個々のカテゴリの相関分析は、そのようにして作られたカテゴリの類似度の分析の方法です。

ラベル分類の方法を使って、「OKとNGの違いは何か？」という分析をすることがありますが、この時にカテゴリの類似度の分析が役に立ちます。

筆者の場合は、決定木と相補的な使い方として、アソシエーション分析を使っていました。

アソシエーション分析は、網羅的にカテゴリの組合せを調べる方法です。

コレスポンデンス分析は、カテゴリを高次元の座標データに変換して、近さを調べる方法です。

上記の方法だと、同じ特徴のあるカテゴリがある時に、「同じらしい」や「似ている」ということはわかるのですが、それは人が見て判断することになっています。

カテゴリの分解分析では、カテゴリを要約しますが、計算によって、グループ分けもします。

カテゴリの類似度の分析では、個々のカテゴリの組合せの数を調べます。

このような組合せについて、テキストマイニングでは、「共起（きょうき）」と呼ばれます。