決定木

決定木（Decision Tree：デシジョンツリー：けっていぎ）は、データの中から注目したい領域を見つける方法です。

決定木は、顧客の分類の分析をするのにぴったりなため、参考書を探すとマーケティング向けのものが多く見つかります。しかし、物事の多様性を整理するのに便利な方法なので、マーケティングに限らず、いろいろな分野で重宝します。

Yのデータが質的データの場合を「決定木」や「分類木」、量的データの場合を「回帰木」と言って区別する場合もあります。このサイトでは、特に区別する必要のある場合以外は、「決定木」にしてあります。

一口に「決定木」と言っても、木の作り方がいろいろあります。例えば、情報量を使うものでは、情報量によって、最良の枝分かれを決めます。

決定木のイメージ

決定木は、何をしているのかがわかりにくい方法だと思います。そのため、何の役に立つのかもわかりにくいです。イメージ作りのためにまとめると、下記のような感じになります。

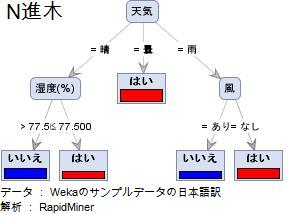
決定木のグラフは、最初は見方がわからないかもしれません。右の図の場合で説明します。

まず、この解析のYは、「はい」と「いいえ」の２値データです。「外出しますか？」についての、「はい」と「いいえ」の違いが、天候の何で決まるのかを調べようとしています。

解析の結果、第１に、「天気」が一番Yの違いに影響していることがわかりました。そして、「晴」の場合は、「湿度」が77.5%を境にして、Yが違っています。また、「雨」場合は、「湿度」ではなく、「風」がYに影響しています。

このデータには、Xとして「温度」というのもあるのですが、「温度」はYに関係ないことがわかりました。

このように、カテゴリによって、有力な因子が異なることを解析できてしまうのが、決定木のすごさです。また、有望なカテゴリを自動的に抽出してくれるのも、決定木のすごさです。多変量解析と呼ばれる手法で、同じ様な解析結果を出そうとするなら、かなり丁寧に層別をする必要があります。

データの仲間分け（分類）の方法として、クラスター分析や、自己組織化マップ（SOM）（以下、分類手法と呼びます。）があります。これらの手法の欠点として、「ソフトが出した結論は正しいのかもしれないが、ソフトがその結論を導いた理由がわからない。」、というものがあります。

決定木には、この欠点を補う使い方があります。

やり方ですが、分類手法の作ったカテゴリーをYにして、分類手法を使った時のXを、決定木で解析します。すると、カテゴリーとXの関係が推測できることがあります。詳しくは、クラスタリングの原因分析にまとめています。

決定木では、枝分かれを必要な程度まで成長させて、枝先の内容を見ます。そのため、どこまで枝分かれさせるかが解析のポイントになります。

枝分かれでは、最初の枝分かれが先の方まで影響します。相関関係の探索で決定木を使う場合は、どこまで枝分かれさせるかだけでなく、最初の枝分かれをどう扱うかも大事なポイントになります。因果関係の分析では、大きな要因から順に枝分かれするのが理想的です。

しかし、分析対象のデータによっては、大きな要因から枝分かれしないです。また、２つの要因で優劣がほとんど変わらない場合は、枝分かれの出発点は、両方を見てみたいのですが、できあがった木を見ても、そのような優劣の状況はわかりません。これらが決定木の弱点です。

弱点の対策の簡単な方法としては、まず、すべての説明変数で木を作ってみて、第一に枝分かれした変数を外して、もう一度、木を作る方法があります。

ランダムフォレストは、決定木の一種です。一般的な決定木も含め、多変量解析やデータマイニングの手法は、一般的に解析対象のデータを一度に処理しますが、ランダムフォレストは、一部のサンプル（一部の行）と、一部の変数（一部の列）のデータの組を、ランダムに複数作り、それらの組を、それぞれ処理します。

複数できた木を見て、総合的に考えます。アンサンブル学習の一種です。

カテゴリの類似度の分析を使うと、決定木で見つける事が難しいような、局所的な変数の関係性を見つけられることがあります。

意思決定論の文献で、「デシジョンツリー」という手法が紹介されていることがあります。このデシジョンツリーは、このページのデシジョンツリーとは別物です。枝分かれしている図になっている点は似ているのですが、どちらかと言えば、 FTA に近いです。

「SPSSクレメンタインによるデータマイニング」　牛田一雄・高井勉・木暮大輔　著　東京図書　2003
ニューラルネットワークは、結果が出ても、そうなる理由がわからない手法なので、ニューラルネットワークの結果を決定木で検討する話があります。

「データマイニング入門　：Rで学ぶ最新データ解析」豊田秀樹　編著　東京図書　2008
自己組織化マップの結果を決定木で検討する話があります。

「知識工学」　小川均　著　共立出版 2005
情報理論を使った木の作り方や、決定木からルールを作成する方法について

「多変量解析法入門」永田靖・棟近雅彦共著サイエンス社 2001
「多段層別分析」というタイトルで、決定木のひとつであるCARTが解説されています。 CARTは二進木です。