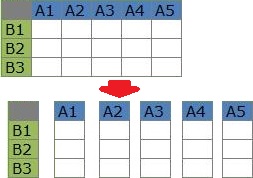
変数の類似度の分析では、データの表を縦に短冊状に切って、短冊同士の近さを見ます。
変数の類似度の分析は、 「変数がたくさんあるけど、分類できないか？」といった感じで、 データマイニング の最初の段階でします。
また、 多変量解析 で、 多重共線性 を考えながら、 変数の選択 をするための分析としても使われます。
量的・質的の違いと、直接的・間接的の違いの２×２の４種類に分けています。
量的・質的の違いというのは、量的変数用か、質的変数用かという違いです。
直接的・間接的の違いというのは、２つの変数の組合せを直接評価して、近いもの同士でグルーピングするのか、 新しく作った変数への近さでグルーピングするかの違いです。
間接的の中には、さらに、 要約分析と分解分析の違い があります。
| 名前 | 量的 | 質的 |
| 直接的 |
多変量データの相関分析 グラフィカルラッソ LiNGAM |
独立性の検定 対数線形分析 連関係数 ベイジアンネットワーク |
| 間接的 |
主成分分析 因子分析 独立成分分析 正準相関分析 行列の分解 |
項目反応理論 連関係数を使った主成分分析 |
量的変数の相関性では、２つの変数で散布図を描いた時に、データが一本の直線に近くなるかどうかで、相関の高さがわかります。 このため、線形の評価になります。
この考え方を、質的変数の相関性で考えると、質的変数の相関性の解析では、非線形を扱っています。
量的変数を １次元クラスタリング で質的変数に変換して、質的な変数の類似度の分析をする方法は、非線形分析の目的でも役に立ちます。
Natto のサイトには、ソフトのダウンロードや、理論の解説があります。
順路
次は
多変量データの相関分析
