トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

独立性の検定

２元分割表はシンプルな 分割表 です。

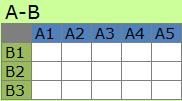
この２元に、「関係（相関）があるのか？」という分析は、「独立性の検定」と呼ばれています。

関係がない場合、表の中の値は、ほぼ均等になるはずです。 独立性の検定では、何らかの関係があると、値が偏って来ると考えます。

独立性の検定が対称とする２元の 分割表 は、２つの質的変数のデータから作られることを考えると、独立性の検定は、２つの質的変数についての類似度（相関）を見る方法と言えます。

２つの変数の組の関係を網羅的に調べるのなら、 変数の類似度の分析 としても使えます。 この使い方は、たくさんの量的変数の関係を見るために、 多変量データの相関分析 をするのと、同じ考え方をしています。

質的なデータの相関性を見る手法だが、応用として量的なデータにも使える

独立性の検定は、２つの質的変数についての類似度（相関）を見る方法です。

ただ、量的なデータに使えない訳ではなく、「0未満、0以上10未満、10以上20未満、20以上30未満、30以上」といった区間データにしてしまえば、 使うこともできます。

この方法のさらなる応用として、「0以上10未満、100以上200未満、1000以上2000未満」 といった感じで、区間に隙間があるデータでも、特に問題なく使えます。

２×２の分割表の場合

２元分割表の中でも、一番シンプルなのが、２×２の分割表です。

２×２の分割表では、

のようにデータが並んでいる場合、Φ（ファイ）（点相関係数）やカイ二乗が、独立性の指標になります。 カイ二乗は、カイ二乗検定で 検定 もできます。

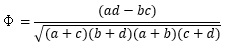
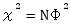
ｍ×ｎの分割表の場合は、カイ二乗の計算は、もう少し複雑になります。 煩雑な計算ですし、ネット上にも、たくさん紹介されていますので、このページでは省略します。

○×の正誤表

○×の正誤表は、 パターン認識 の精度の評価にも使われます。

分割表 のページにあるような例だと、２元の相関を考えることは、あまり重要ではありませんが、 正誤表のような分割表だと、相関は重要です。 相関がないということは、答えがデタラメということになります。

計算例

２×３の分割表の場合　その１

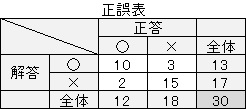
２×３の分割表で試してみます。

まず、左側の表の６個のデータは、あまりばらついていません。 この場合がp値がほぼ１です。

右側の表は、１個のデータだけが特に大きいです。 この場合がp値がかなり小さくなっています。

２×３の分割表の場合　その２

違うタイプの２×３の分割表で試してみます。

左右の表は、一番右の列の数字が逆になっているだけですが、右側の表の方がp値がかなり小さいです。 行方向と列方向の項目の何かの相関があると、p値が小さいことがわかります。

９×７の分割表の場合　その１

表のサイズを大きくしてみます。 右の表に行くほど、データのばらつきを大きくしてみます。

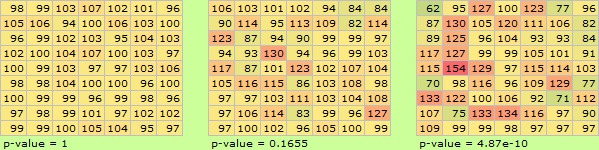
データのばらつきが大きくなると、それに伴ってp値も小さくなっています。 p値の大きさは、ばらつきで変わっていることがわかります。

ばらつきの大きいことがポイントになる場合に、ばらつきを測る方法として良いかもしれません。

行方向と列方向の項目が、２、３個しかなく表のサイズが小さい場合は、相関性を見る方法として独立性の検定は使えますが、 表のサイズが大きいと、この方法で値の規則性を見つけるのは難しいです。

９×７の分割表の場合　その２

表のサイズは９×７で同じなのですが、極端に値の高い場所がある場合です。

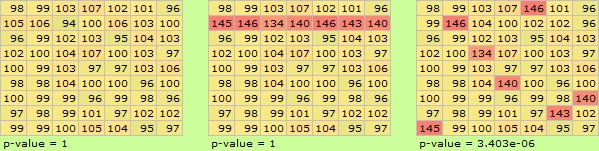
左側の表は、あまりばらついていません。 この場合がp値はちょうど１です。 中央の表は、ひとつの行だけ値が高めです。 この場合もp値はちょうど１です。 右側の表は、中央の表の数字を入れ替えてみたものです。 p値は、かなり０に近い値になっています。

その１で、「ばらつきの尺度」と書きましたが、特定の行だけが値が高くてばらつきが大きい場合は、この尺度では測れない事がわかります。

ソフト

R

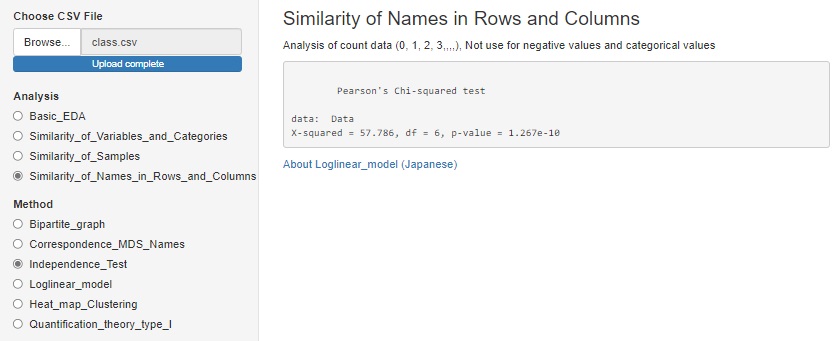
Rの実施例は、 Rによる違いの有無の分析 にあります。 上記の計算例も、このページのコードを使っています。

R-EDA1

棒グラフとセットにした分析

R-EDA1 では「Stratifeid_graph（層別のグラフ）」を選んで、「bar（棒グラフ）」を選ぶと、 グラフを描くために選んだ変数を使って、独立性の検定ができます。 ２つの質的変数で分割表を作って、検定をするまでの手順が自動になっています。

分割表の分析する

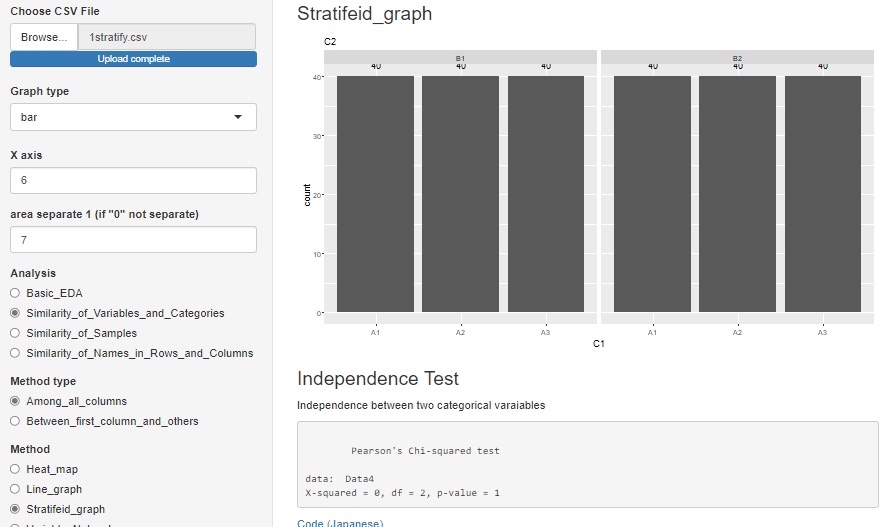
分割表にすでになっているデータを分析する場合は、上記とは違う場所になっています。

参考文献

「統計解析ハンドブック」　武藤真介　著　朝倉書店　1995
ユールの連関係数　Q = (ad - bc) / (ad + bc)
Φ係数（四分点相関係数・点相関係数）、ピアソンの連関係数　クラメールの連関係数

「独習統計学24講　すべての医療系学生・研究者に贈る 応用編」　鶴田陽和　著　朝倉書店　2016
独立性の検定として、尤度比検定、Fisherの正確検定、カイ二乗検定を説明し、それらの使い分けの話もあります。 使い分けについては、人によって解釈の違うところもあるそうです。

「カテゴリカルデータ解析　Rで学ぶデータサイエンス」　藤井良宜　著　共立出版　2014
指標は、ピアソンの一致性係数、クラメールのV統計量。
一般化マンテル検定、クラスカルワリス検定、マクマネー検定、オッズ比の均一性の検定など。

「調査法講義」　豊田秀樹　著　朝倉書店　1998
連関指標として、
比率の差d = a/(a+c)-b(b+d)
、ユール、四分点相関係数を紹介。
共通原因がある場合、第３の変数で層別してから、相関を確認すると良い。

「多変量データ解析法　理論と応用」　柳井晴夫　著　朝倉書店　1994
φは-1から1となり、ファイ相関係数や、点相関係数と呼ばれる。

「品質工学の数理」　田口玄一　著　日本規格協会　1999
Φの２乗と同じ計算式になっている指標を独立性の評価に使っています。
ｍ×ｎの分割表の場合は、「１つのカテゴリ　対　多のカテゴリ」の分割表と考え、あるカテゴリ以外は合計してしまいます。 こうすることで、２×２の分割表の計算が使えるようにします。 カテゴリに順序がある場合、カイ二乗よりもこの計算の方が、人の感覚に近い評価ができるそうです。

多元表の分析

「グラフィカルモデリング」　宮川雅巳　著　朝倉書店　1997
独立性の検定は、２元分割表の相関分析ですが、この本では３元以上の相関分析の方法も紹介されています。 対数線形モデル（生起確率の対数をYにした、交互作用項を含む線形モデル）にして、 多変量データの相関分析 に持ち込んでいます。

「分割表の統計解析　二元表から多元表まで」　宮川雅巳・青木敏　著　朝倉書店　2018
同著者の上記の本から、さらに多元分割表からの相関分析の方法を研究した内容になっています。

すべての質的データの組み合わせ

量的データについては、すべての変数の組み合わせの相関係数を計算して、行列の形にした「相関行列」がよく知られています。 これと同じように質的データについてはも、すべての変数の組み合わせを計算して、連関係数の行列を作るアイディアがあります。 相関行列とは違って、いったんすべての組み合わせについて、 分割表 の形にデータを変換してから連関係数を計算します。 この実施例については、下記のサイトにありました。

「R　大量のカテゴリ変数から変数間の連関度を表すクラメールV指標を計算し、有意で連関があるペアのみ抽出する」　武田祐子　氏　2016
https://qiita.com/ytakeda/items/058e83ebdd721f87ceb4

順路 次は 対数線形分析