パターン認識
では、真の値は〇で計算値も〇、真の値は×で計算値は×なら、完璧ですが、実際には、〇を×と予測することや、×を〇と予測することもあります。
これをまとめた表は、「混同行列」（confusion matrix）と呼ばれます。
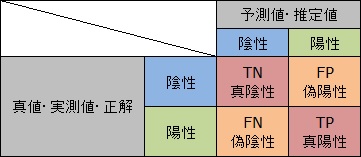
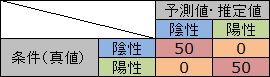
完璧な認識ができる場合、左上と右下だけに数字が入ります。
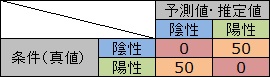
必ず間違える認識になっている場合、左下と右上だけに数字が入ります。
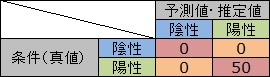
左上だけや、右下だけに数字が入っている場合、真値が片方の場合は完璧な認識ができているので、 「完璧だ」と思いたくなります。 しかし、もう片方の時についてはデータがないので、何とも言えません。
現実の世界では、真値が片方しかない場合がありますので、注意が必要です。
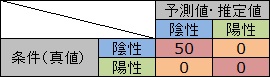
パターン認識では、必ず正しい判定の出る仕組みを作れることは、ふつうはありません。 どんなに工夫しても、ある程度は判定を間違えてしまいます。 そうすると、混同行列の右上や左下にも０以外の数字が入って来ます。
こうなって来ると、正解と不正解の比率を計算して評価することになって来ます。
一番簡単な指標が精度です。
精度 = (TP + TN) / (TP + TN + FP + FN)
となっていて、当たったもの比率になります。
精度では、間違いの種類がよくわからないため、もう少し細かい指標があるのですが、 分野によって注目したいものが異なるため、 混同行列から計算する指標は変わって来ます。
リスク
に注目する分野では、
偽陽性率 = FP / (TN + FP) 本当は陰性の人を、「陽性」と判定してしまう割合
偽陰性率 = FN / (TP + FN) 本当は陽性の人を、「陰性」と判定してしまう割合
の、２つの指標を２種類のリスクと考えて、注目します。
ちなみに、偽陽性率、偽陰性率は、 統計学 の 検定 で、「 第１種と第２種の誤り 」と呼ばれているものと考え方は同じです。
検定 の理論では、分布を仮定して、分布の面積を求めることでこの確率を求めますが、 パターン認識 では、分割表のデータから求めることが一般的になっています。
偽陽性率 = FP / (TN + FP) 本当は陰性の人を、「陽性」と判定してしまう割合
真陽性率 = TP / (TP + FN) 本当は陽性の人を、「陽性」と判定する割合
という、２つの指標に注目する分野もあります。
「スクリーニング」と言われますが、精密な方法で調査をする前に、大雑把な方法で、精密な方法が必要かどうかを確認する時に使われる考え方です。
スクリーニングでは、本当は陽性の人は100%「陽性」と判定したいです。 次に、本当は陰性の人を「陽性」と判定してしまって、精密な調査を受けることはできるだけ避けたいです。 つまり、「まず、真陽性率はできるだけ大きくしたい。しかし、偽陽性率はできるだけ小さくしたい」と考えます。
この２つの指標が閾値によって変わる場合ことも考えて、パターン認識の精度を評価する方法が ROC曲線とAUC です。 機械学習 の解説では、よく出て来ます。
上記のように、偽陽性率は、検定の理論の第１種の誤りに相当します。 真陽性率は、 検出力 に相当します。
何かの測定器で測った数字や、何かの計算式で計算した数字が下図だったとします。
陽性と陰性の条件を変えた時の結果が、数字になっています。
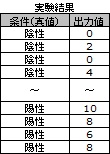
このデータを整理すると、下図のようなグラフになります。
条件が陽性の時の方が値が高めですが、陽性と陰性で同じ値になる時もあることがわかります。
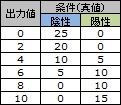
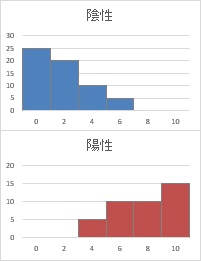
例えば、判定値を3にして、3以下の時に「陰性」と判定することにします。 条件が「陰性」で3より低い時は、出力値が0の時の「25」と、出力値が2の時の「20」になりますので、 混同行列の左上のマスは、45 (= 25 +20）になります。
このようにして混同行列を作ると下図になります。
判定値が3の時は、本当は陽性の人が陰性と判定される状況が起きていません。
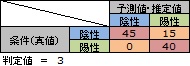
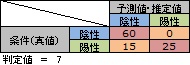
判定値を7にすると、混同行列は下図になります。
混同行列は判定値で変わることがわかります。
判定値が7になると、本当は陽性の人が陰性と判定される状況が起きています。
混同行列があった場合、「どういう判定方法で、この行列を作ったのだろう？」、という風に考えると、 深い分析ができることがあります。
「1/2」と、「10/20」は、どちらも0.5ですが、「10/20」から計算された0.5の方が、統計的には信頼できる数字です。 信頼性が低い場合は、リスク的に安全な数値の方が望ましいことがあります。
推定 の理論では、データの数による信頼性を計算に含まれています。 また、比率の計算について、 比率の差の検定 のように、「1/2」と「10/20」の違いを考えている理論もあります。
ところが、筆者の知る限りでは、 パターン認識 の文献では、一般的に「1/2」と「10/20」の違いは考えません。
抜き取り検査 のページに予測歩留の計算方法がありますが、これは、リスクも評価してこうした確率を計算する方法です。
この計算をする場合は、混同行列に集計する前の、出力値のデータを使います。
「Pythonではじめる機械学習 scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎」 Andreas C.Muller, Sarah Guido 著 オライリー・ジャパン 2017
混合行列から２つの指標を計算して使う方法として、上記の２種類以外では、この本では、
適合率 = TP / (TP + FP)
再現率 = TP / (TP + FN) (＝真陽性率）
として、適合率・再現率カーブを評価する方法も紹介されています。
F値は
F = 2 * (適合率 * 再現率) / (適合率 + 再現率)
で、総合的な指標としては、精度よりも良いそうです。
データに偏りがある場合の例があります。
多値の場合も、精度、適合率、再現率を見る。
「フリーソフトではじめる機械学習入門」 荒木雅弘 著 森北出版 2014
同じ指標について、上記の本よりも、コンパクトに解説
順路
次は
ROC曲線とAUC
Tweet
