パス解析

データ解析では、ひとつの Y に対して X が複数あり、さらに、X であるものが、別の X の Y になる場合があります。 X と Y がネットワークの構造を持っています。パス解析は、このようなデータを解析する方法です。

パス解析は、重回帰分析の集合を扱う手法です。

パス解析の進め方

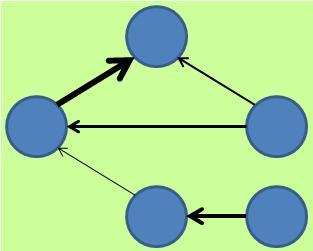
パス解析では、まず、自分の経験則や仮説に基づいて、各変数についての目的変数と説明変数の関係（因果関係）を考え、パス図を作ります。図にパス図のイメージを書きましたが、矢印の元が説明変数で、先が目的変数を表します。

次に、各パス間で重回帰分析を行い、パス間のつながりの強さを、標準偏回帰係数で評価します。

パス解析の中に、潜在変数（データはないけれども、持っているデータに関係していると考えている変数）を入れるのが、共分散構造分析です。パス解析の発展型と言えますし、因子分析の発展型とも言えます。

パス解析は自分でパス図を作るところから始まる方法です。「パス図は、こうなっている」という仮説を元にして、仮説の検証（実証分析）をするための方法として開発されています。

仮説作りは、扱っている事象の原理原則に基づくのが基本的ですが、データから仮説を探索的に見つける方法が下記になります。

LiNGAM は、パス図を自動で作ってしまう方法になります。さらに、パス解析で重回帰分析をする部分も、一緒にやってしまう方法になっています。

つまり、データセットを与えると、パス図の仮説を作るところから、重回帰分析のモデルの係数を求めるところまでやってくれる方法です。

ただ、 LiNGAMの限界にあるように、うまく求められない事がけっこうあります。

正規化による有向相関分析やハイブリッド有向相関分析をすると、パス図（有向グラフ）が自動で求まります。

これさえできれば、従来のパス解析（重回帰分析のモデルの係数を求める）ができるようになります。

LiNGAMよりも手間は多いですが、前提とする仮説の確からしさは、こちらのアプローチの方が良いです。