Rによるデータ分析

Rによるクロス集計表の散布図分析

A-B型の分析 として、 クロス集計 の分析方法です。

分割表の特徴をグラフで直接見る方法になります。

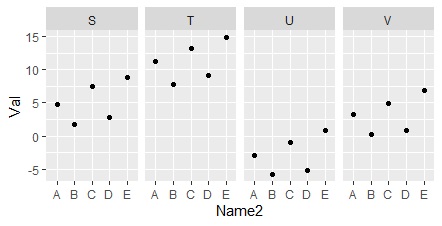
層別の１次元散布図

層別 の １次元散布図 を使って、体系的なグラフにする方法です。

library(tidyr) # ライブラリの読み込み
library(ggplot2) # ライブラリの読み込み#
setwd("C:/Rtest") # 作業用ディレクトリを変更
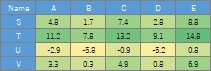
Data <- read.csv("Data.csv", header=T) # データを読み込み
Data1 <- tidyr::gather(Data, key="Name2", value = Val, -Name) # 縦型に変換（Nameの列以外を積み上げる）
ggplot(Data1, aes(x=Name, y=Val)) + geom_point() +facet_grid(.~Name2) # 層別の１次元散布図

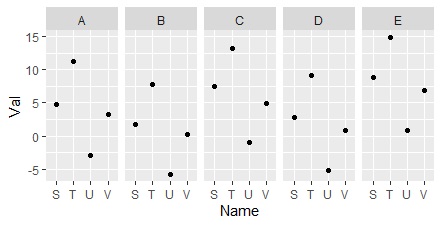
NameとName2を入れ替えると、グラフの分け方が入れ替わります。
ggplot(Data1, aes(x=Name2, y=Val)) + geom_point() +facet_grid(.~Name) # 層別の１次元散布図

Rによるデータ分析