トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
複雑な動きをしている折れ線が10種類あります。
ヒストグラム
を見ると、平均値の位置も、ばらつきの仕方もかなり違います。
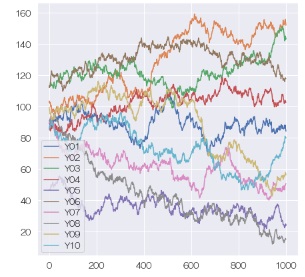
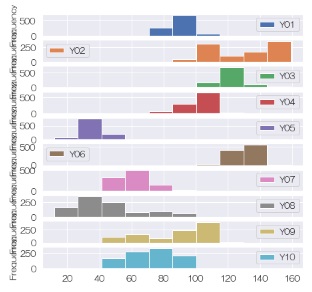
それぞれの変数について、ひとつ後の値との差を計算して、 差分データ を作ります。
すると、複雑に見えていたデータですが、差分データにすると、同じ現象らしいことがわかります。
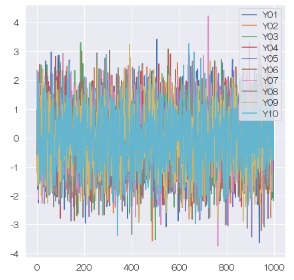
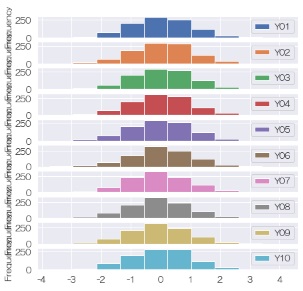
差分データは
ノイズ
に見えますので、差分データのモデルは
差分（＝X(t+1) - X(t)） ＝ 平均が０で標準偏差が１くらいになっている正規分布の乱数
になっているらしいことがわかります。
よって、元のデータは、
X(t+1) ＝ X(t) ＋ 平均が０で標準偏差が１くらいになっている正規分布の乱数
であることがわかります。
実際、このモデル式で、このデータを作っていますので、この推測の仕方は正解です。
このモデルでは、次の位置が、元の位置を基準にしたランダムな位置になります。 「ランダムウォーク」、「酔歩」、「千鳥足」と呼ばれます。 なお、ここでは、次の値がプラス側にもマイナス側にもランダムに決まり、移動量がランダムな正規分布になっているモデルで、 ウィーナー過程と呼ばれています。 ランダムウォークモデルと呼ばれているものには、移動量は一定で、向きだけがランダムなものもあります。
ランダムウォークモデルは、 時系列 の ばらつきモデル の中では、とてもシンプルなものです。 ランダムウォークモデルで作られるデータは 正規分布 ではありませんが、 正規分布から作られる分布 の一種になります。
ランダムウォークモデルは、とてもシンプルです。 使い方がいくつかあります。
ランダムウォークモデルは、株価のモデルとして知られています。 株価のモデルになる理由は、いくつかあるようです。
ただし、株価とは似ていないところもあります。
まず、株価のデータは、1秒ごとや1日ごとの単位時間のデータなので、その単位時間の間で起きていることはわかりません。 私たちが見ているのは、単位時間ごとの間が欠損したデータです。
そのため、実際のデータに、ランダムウォークモデルを適用している時は、欠損値を削除した分析をしていることになります。
ランダムウォークモデルになっていれば、 自己相関 も高くなって来ます。
自己相関が高いと、 現在のデータを次のデータの予測値にする方法が使えるようになります。
さらにランダムウォークモデルと言っても良い状態なら、 次のデータの予測値は、中心値が現在のデータになることだけでなく、そこからどのくらいばらつくのかもわかります。
ばらつきが予測できるので、次の値が実際に取れた時に 外れ値かどうかの判定 ができます。
SARIMAXモデル などの中にある「I」というのは、 Iモデル のことです。
元のデータを見ると、「どうしようか・・・」となるような現象でも、差分が、何らかの分布になっている場合は、 見通しの良い分析ができるようになります。
UとVという独立した変数があるとします。
独立の定義は、
P(UV) = P(U)P(V)
です。
独立していると、共分散は0になります。
共分散が0ということは、相関係数は分子が共分散なので、相関係数も0になります。
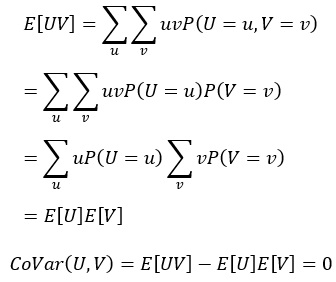
話は変わりますが、UとVから作られるXとYという2つのランダムウォークがあったとします。
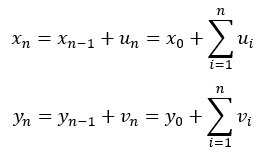
以下からわかるように、XとYにも独立の関係があります。
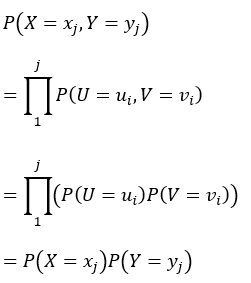
そのため、XとYの相関係数は0になるはずですが、実際はそうなりません。 「XとYが独立、かつ、サンプル数は十分多い」となっていたとしても、相関係数は0にはならず、-1から1まで幅広い値になります。 この現象は、「見せかけの回帰」と呼ばれています。
順路
次は
母数変動型ランダムウォークモデル
