トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
ARモデルとMAモデルは、それぞれが違う観点で、 重み付き移動平均モデル の応用になっています。
ARMAモデルは、 ARモデル と MAモデル を合体したモデルです。
式は、以下のようになります。
ARモデルとMAモデルを、足し合わせた形です。
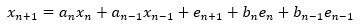
結論からですが、「ARMAモデルは、実務向きではない」というのが筆者の認識です。
まず、 ARモデル と MAモデル のそれぞれのページに説明していますが、ARとMAの単体が、実用性に乏しいモデルになっています。
ARMAモデルは、数学的にはARとMAが相反する特徴を持っているので、両者を合わせることで、両者の長所が使えることを狙っているようなのですが、それはあくまで数学的な側面についてで、実用性に改善は見られないです。
「計量経済学」 西山慶彦 他 著 有斐閣 2019
自己相関や、モデルのサイズの決め方。
「経済の時系列分析 」 山本拓 著 創文社 1988
AR、MAの平均、分散、自己共分散。ラグ・オペレーターによる表現。係数の推定。Box-Jenkinsによるモデルの作り方。
ARMAモデルによる予測は、データの範囲よりも離れると、データ全体の平均に収束するので、時系列の予測として意味があるのは短期的な予測だけなことが書かれています。
「実証のための計量時系列分析」 ウォルター・エンダース 著 有斐閣 2019
定常性や自己相関について説明した後で、Box-Jenkinsによるモデルの作り方と予測。
「時系列解析」 柴田 里程 著 共立出版 2017
「弱定常時系列」という観点で、表現方法や性質を説明
「将来予測と意思決定のための 時系列分析入門 様々な時系列モデルによる予測方法からその評価方法まで」 長倉大輔 著 ソシム 2025
「自己回帰移動平均モデル」と言う名前で、ARMAモデルが解説されています。
13章まである内の、10章まではARMAモデルを頂点として、そこまでの道のりを丁寧に解説しています。
残りの章で、
ボラティリティ推定モデル
や
カルマンフィルタ
を補足のようにして解説しています。
「現代時系列分析」 田中勝人 著 岩波書店 2006
ARMAの自己相関や、スペクトル解析について。
順路
次は
ARモデル
