移動平均モデル

移動平均は、時系列近傍法の基礎モデルとしてではなく、ノイズを除去する方法としての方が、よく知られているようです。このページは前者の使い方についてですが、後者の使い方は、移動分析のページで説明しています。

移動平均モデルによる予測

ホワイトノイズモデルは、過去のデータの全部を使って平均値を計算して、予測値にします。ランダムウォークモデルは、直前のデータだけを使って、予測値にします。

移動平均モデルは、これらの中間で、例えば、３ステップ前までの値の平均値を計算して、予測値にします。

下のデータは、最高気温のデータです。7日までのデータがあり、8日の最高気温を予測する問題を考えます。気温の場合は、天気にも左右されるので、前日だけではなく、直近の数日のことを考えた方が良さそうですが、このような考え方は、移動平均モデルの考え方です。

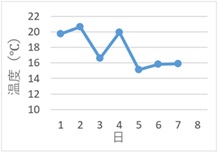
ベースになる値がゆっくりと変化していて、観測しているのがベースの値に誤差が加わったものの場合、直前の１つの観測値だけを見るよりも、直近の複数の観測値の平均値を見た方が、ベースの値を精確に推定できます。移動平均モデルは、このような場合に適しています。

ちなみに、ホワイトノイズモデルは、ベースになる値は変化していないことを前提としたモデルです。ランダムウォークモデルは、ベースになる値が頻繁に変化していることを前提としたモデルです。

直近の3個のデータで計算するのなら、n番目の移動平均は、以下になります。
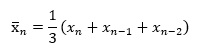
移動平均モデル

予測モデルの式は、以下のようになります。
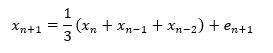
移動平均モデル

３個のデータの移動平均は、３個のデータの合計を、３で割ります。その式を変形すると、下記のようにもなります。「それぞれのデータに、1/3をかける」という式になっています。 1/3が３個あるので、合計は１です。
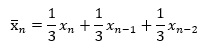
移動平均モデル

この変形を一般化すると、下記になります。
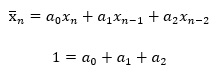
移動平均モデル

この変形をすると、例えば、「a0 = 0.4、a1 = 0.3、a2 = 0.2にして、直近のデータを重視する」といったモデルになります。このようなモデルを、「重み付き移動平均」と言います。

指数平滑法、ARモデル、MAモデルは、重み付き移動平均を、さらに発展させた方法になっています。

指数平滑法は、「直近ほど重視」と「多くのデータを使う」ということを実現する方法です。「合計が１」という制約は使います。

ARモデルは、「合計が１」という制約も外して、係数を自由に設定できるようにしたモデルです。

MAモデルは、観測しているデータ重み付き移動平均ではなく、観測していないデータ（誤差）についての、重み付き移動平均を想定するモデルです。