トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

ばらつきモデル

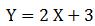
という式なら、Ｘの値が変わったら、Ｙがどのような値になるのかを シミュレーション するのは、簡単です。

この式のＸに、0から2までを0.1刻みで代入すると、下図のような結果になります。

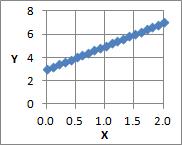
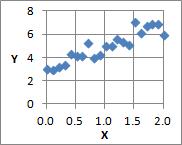
しかし、現実のデータは、下図のようになっている事が多いです。 だいたいこの式になっていても、 誤差があるので、Ｙは多少ばらつきます。

統計学 は、このばらつきを扱うのに優れていて、ばらつきの部分を表現するのに、

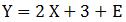
のようにして、「Ｅ」という部分を足します。 「Ｅ」は、Error（エラー：誤差）のことです。 構造方程式 では、Ｅを意識して扱います。

では、「Ｅのある式は、どうやってシミュレーションするのか？」、というのが、このページのお話になります。

統計モデル風の数理モデル

統計モデル では、数式の中にＥが書かれていることがありますが、象徴的です。 実際に計算して求めるのは、Ｅの入っていない式です。

予測のためのソフトの使い方 がありますが、Ｅを加味した計算結果は出ません。 そのため、例えば、「入力値がある値で一定の場合に、標準偏差がどのくらいになるのか？」といった予測はできません。

そこで、Ｅを加味した計算をするには、Ｅの部分を考慮した 数理モデル としてシミュレーションします。

Ｅの作り方

Ｅは「誤差」なので、平均値が０の正規分布になっていると仮定する方法が手軽です。 ばらつくデータの作り方 を使って、平均値が０の正規分布になるデータをたくさん作り、それぞれをＥに代入して、Ｙがどのような分布になるのかを見ます。

正規分布になるデータは、平均値を０と仮定するのは良いとしても、標準偏差をどうするのかが考えどころになります。 測定器の測定誤差等、実際に起きているばらつきを考慮して標準偏差は決めます。

計算のサンプル

このシミュレーションは、説明だけ読んでも、イメージがわきにくいと思いますので、 サンプルファイル も作りました。 このファイルを使うと、冒頭の２つの図のデータも作れます。

サンプルでは、Ｘは均等の刻みにしてあります。 実際のデータに近くするには、Ｘも乱数で作った方が良い事もあります。 つまり、ＸとＥの両方が乱数で作られ、様々Ｘ（入力のばらつき）とＥ（出力のばらつき）の組み合わせから生み出されるＹを調べることになります。 こうすると、入力のばらつきと、出力のばらつきの両方の影響を調べることができます。

ばらつきモデルの使い道

ばらつきモデルのシミュレーションは、式が複雑な時に、特に役に立ちます。

予測区間のシミュレーション

Ｙが複雑な計算式でできているものだと、 予測区間 も複雑になりますが、シミュレーションで計算した数字をグラフにすると、予測区間がどのような分布なのかを把握できます。

誤差のシミュレーション

誤差解析 では、Ｙの標準偏差はわかっていて、要因の標準偏差がどの程度なのかを推定したい事があります。

例えば、Ｘが２つある場合は、 それぞれのＸについて、標準偏差を３通りずつ仮定してみて、 その標準偏差の組み合わせのそれぞれについて、Ｙの標準偏差をシミュレーションで求めてみます。 そうすれば、シミュレーションで求めたＹの標準偏差と、実際の標準偏差の差が一番小さい値になる、Ｘの標準偏差の組み合わせではないかと、 推定できます。

順路 次は ばらつくデータの作り方