トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

予測とシミュレーション

モデル式
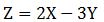
という数式が、何かの現象を表しているとします。

すると、この数式は
「Xが3で、Yが1になる時は、Zは3になりそう」、といった予測に使えます。 また、XやYにいろいろな値が入った時のZの値を見ることで、シミュレーションにも使えます。

モデリング

データサイエンス では、現象を何らかの数式やルールで表現したものを「モデル」と呼び、 モデルを作ることを「モデリング」と呼びます。

モデリングには、大きく分けて 統計モデリング と 数理モデリング があります。 統計モデリングは、 誤差 があるデータでも、だいたい当てはまるように作るモデルです。 数理モデリングは、「現象の数式は、こういう形かもしれない」、と仮説を立てて、 検証していくことで作るモデルです。

統計モデリングと数理モデリングは、完全に別のアプローチではなく、 汎用性の高い数理を取り込んだ統計モデルがありますし、 数理モデルの特定に統計的な方法が使われることもあります。 両者の間に入るものとしては、 データフィジクス（データ物理学） が重要です。

シミュレーション

シミュレーションは、コンピュータを使って実験をする方法です。 （Simulation なので、片仮名で書くと、「シミュレーション」です。 「シュミレーション」ではありません。念のため。。。）

、等々、魅力がいろいろあります。

数値的解析

シミュレーションによる解析は、「数値的に解く」という言い方もします。

ちなみに、紙の上で方程式の変形のようなことをする計算は、 「解析的に解く」と言います。 優先順位としては、解析的に解く方が先で、ダメなら数値的に解析するのが基本です。 「法則」のようなものは、解析的に解いた方がすっきりしたものを見つけられます。

シミュレーションは、解析的に解けない難解な式の性質を調べるための方法でもあります。

「シミュレーション」いろいろ

コンピュータを使って、現象の時間的な変化を調べるシミュレーションは、 「コンピュータシミュレーション」と呼ばれることもあります。

科学の世界では、 原子・分子の世界 や カオス など、様々な分野で使われています。

ところで、ビジネスの世界では、 机上での「試算」や「見積り」を「シミュレーション」と呼ぶことがあります。 どちらの「シミュレーション」なのかに気を付けていないと、 誤解したり、されたりします。

また、 統計学 関係の文献やソフトの中では、 モンテカルロ法 によるシミュレーションのことを、「シミュレーション」と呼んでいることもあります。

CAE

「CAE」は、「Computer Aided Engineering」の略です。 日本語に訳すと、「コンピューターの支援による工学」ですが、一般に日本では「CAE」と呼ばれています。

CAEは、伝熱、流体、応力、等をシミュレーションする分野です。 このサイトで言うと、 流体力学 、 物質のエネルギー 、 物質の変形（連続体力学） にあるような学問の中にある方程式が相当します。

有限要素法

有限要素法は、偏微分方程式の解法として使われます。 使い道は、構造力学、熱伝導、流体力学、等、かなり広いです。

空間を扱う数値計算の分野では、 計算したい領域を細かな領域に分けて解いていきますが、有限要素法もこの点は同じです。 有限要素法は、単純に微分方程式を差分方程式にして、離散空間を計算するのではなく、 変分法を使った式を作ってから離散化していきます。

ランダム実験

統計学 の文献では、統計データがおかしい時の理由として、 データの集め方に偏り（バイアス）がある事を指摘することがあります。 因果推論 の文献では、 この対策として、「データはランダムに集めて実験するのが理想」 、と言われています。

実際にランダムに大量のデータを集めるのは、大変ですが、 ばらつきモデル のページあるように乱数を使って、たくさんのケースを計算してみる事で、シミュレーションしてみる事ができます。



参考文献

「新Excelコンピュータシミュレーション　数学モデルを作って楽しく学ぼう」　三井和男　著　森北出版　2010
物理学や生物学のいろいろなものを扱っています。 Excelだけ、しかも、マクロはできるだけ使わないで、試せるようになっています。
微分方程式ベースと、ルールベースに大きく分かれています。 微分方程式は、差分方程式の形で式を作って、シミュレーションができるようにしています。


「計算物理学　コンピュータ支援による物理学の新しい展開」　日本物理学会　編　培風館　1991
分子動力学法 ・ カオス ・ モンテカルロ法 ・ 素粒子・原子核・宇宙（星）・流体・結晶・神経回路網・形態形成・ 界面・ガラス・水、等々のシミュレーションを、コンパクトにまとめた本です。


「工学シミュレーションの品質保証とV&V」　白鳥正樹　他　著　丸善出版　2013
V&Vは、VERIFICATION（検証）と、VALIDATION（妥当性確認）です。 工学シミュレーションの品質保証について、最新の動向などについてまとめています。 ISO9001に沿った考え方も紹介しています。
（シミュレーションはあくまでシミュレーションなので、 シミュレーションを現実の世界でどのように使うのかについては、 品質保証の分野で新しい考え方が必要になっています。 筆者は、こうした品質保証の必要性について、この本を読むまで気にしていませんでした。）

有限要素法

「非構造分野における有限要素法の基礎」 原武久 著 昭晃堂　1981
一、二、三次元と、段階を追って丁寧に解説しています。補間関数が詳しいです。
・有限要素法では、微分方程式の汎関数を求め、汎関数の極値を取る。
・汎関数を求められない時は、ガラーキン法
・Yを補間関数の和で近似する。


「図解入門よくわかる 最新 有限要素法の基本と仕組み」　岸正彦　著　秀和システム　2010
有限要素法とは何かと言った、数学的な話がないです。 シミュレーションをする時の実際的な話が中心になっています。




順路 次は 統計モデルによる予測

データサイエンス教室