-->
高次元を２次元に圧縮して可視化する方法を使うと、 サンプルの類似度の分析 ができます。
２次元にすることによって、データの様子を見ることが簡単になり、データの特徴をつかみ易くなります。
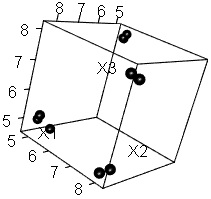
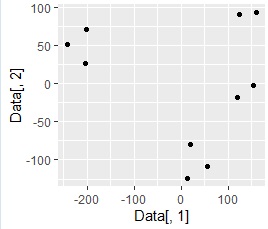
下の例は、３次元データを２次元に変換した例です。
４つのグループにサンプルが分かれていることが、
２次元散布図
で簡単にわかるようになっています。
なお、変換前のデータはもっと高次元でもできます。
-->
たくさんの列（説明変数）があるデータを ２次元散布図 を使って調べる時には、 一般的には、２列ずつの組み合わせを順に散布図にします。
高次元を２次元に圧縮して可視化する方法でも散布図を作るのですが、この散布図には、２列ではなく、すべての列の情報が入っています。
「高次元データを２次元データにする」という説明では、ピンと来ないかもしれませんが、 本来であれば２列しか表現できないはずの散布図に、たくさんの列の情報を描いてしまうのが、すごいです。
ブレーンストーミングの後に、 出てきた意見を似ているものでグループに分けてみたり、 何かのコレクションを、似ているもので近くに置いてみたりする事がありますが、 この２次元マップは、その発想に近いです。 つまり、近い場所にあるかどうかは意味があるのですが、マップ上のどこにあるのかには、あまり意味がありません。
A-B型の分析 の 行列の分解 や コレスポンデンス分析 では、AとBの項目について、共通の尺度で測れるようにしますが、この尺度が多次元です。
このデータを散布図で見るための方法が 多次元同時付置図 になります。
このページは、高次元を２次元に圧縮して可視化する方法としてまとめたものですが、 このページの手法は、「次元削減」や「多様体学習」の手法として紹介される方が一般的です。
次元削減の手法として使う時は、必ずしも２次元まで圧縮する必要はなく、 中間層 として使って、モデルの計算負荷を減らしたり、モデルをわかりやすくするために使います。 この目的で使う時は、 「多少無理があってでも、高次元データを２次元データに圧縮する方法」よりも、 主成分分析 の方が、使いやすいです。
「高次元を２次元に圧縮して可視化する方法」としては、 主成分分析 よりも、「多少無理があってでも、高次元データを２次元データに圧縮する方法」の方が良いので、優劣が逆転しています。
多様体学習の手法としては、スイスロールのようなデータを２次元で表現するために使っています。
筆者は、製造業や工場の中のデータを扱うことが多いです。 スイスロールのようになっているデータはあるにはありますが、 多様体学習のような使い方はしないので、多様体学習の手法としては使い道が思いつかないでいます。
高次元を２次元に圧縮する方法 は、パラメータを変更すれば、３次元や１次元にも圧縮できるようになっていることもあります。 特に指定しなくても使える方法は、デフォルトが「２」になっています。
３次元に圧縮する場合は、次元圧縮としての使い道はあるかもしれませんが、「マップで見る」という使い方には不向きです。
１次元に圧縮する場合は、「グループに順番を付ける」という使い道ができそうですが、 なんの指標もなく、高次元を１次元に圧縮したデータは、１次元の値に意味がないので、順番を付ける使い方ができません。 それもあり、１次元への圧縮も積極的に使う用途がないように思っています。
なお、上記は、１次元の量的データに圧縮する時の話です。 高次元の量的データを、１次元の質的データに変換する方法としては、 クラスター分析 があります。 １次元にするのなら、質的データの方が使い道があります。
順路
次は
高次元を２次元に圧縮する方法
