トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
変数の選択 のページは、変数が多い場合の進め方です。
実務的な 重回帰分析 では、重要な説明変数は１個のことが一番多く、次が２個の場合です。 ３個以上が問題になるようなことは、あまりありません。 あったとしても、考察が難しかったり、データの質と量が不十分なので、分析できないことが多いです。
そうすると、「重要な説明変数は１個か？２個か？」、「２個だとすれば、それらと目的変数は、どういう関係なのか？」といったところが、注目するポイントになります。
このページは、説明変数が２個の場合について、モデルの推定の仕方を説明します。
符号反転の事例集
のページでは、説明変数が２個の重回帰分析について、パターンを12通りに分けています。
下の表は、それらのパターンのどれになるのかを、データから推定するためのガイドです。
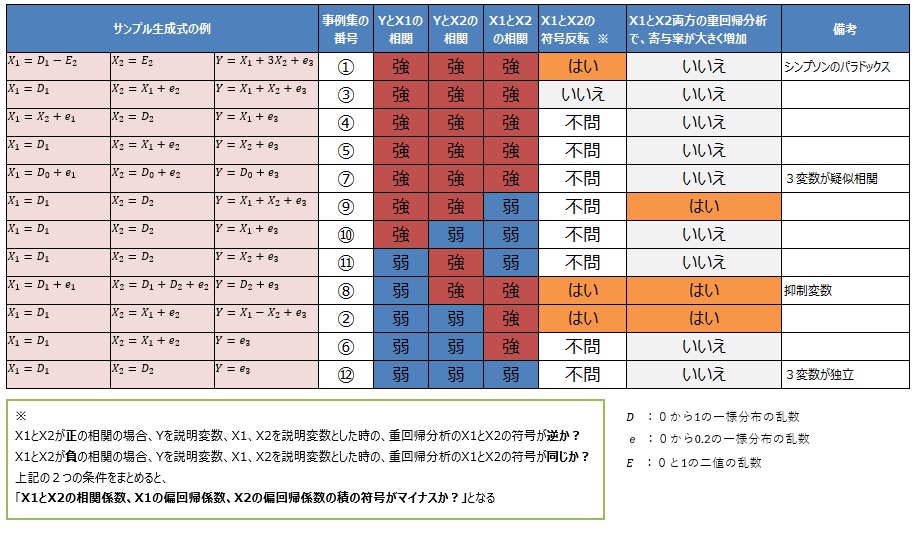
相関を「強・弱」という表現をしています。 目安としては、0.7で良いですが、絶対的な条件ではないです。 実際のデータの様子をグラフで確認して、総合的に判断する必要があります。
以下は、実際のデータに対して、上記のガイドに従って、モデルを推定した例です。
データを作ってから、それに対してガイドを当てはめる手順です。
なお、この例は、誤差eが小さめなので、ガイドの通りに進むと、正解に行き着けます。 現実のデータでは、誤差がもっと大きいことがありますが、その場合は、単純にガイドの通りにはならないです。
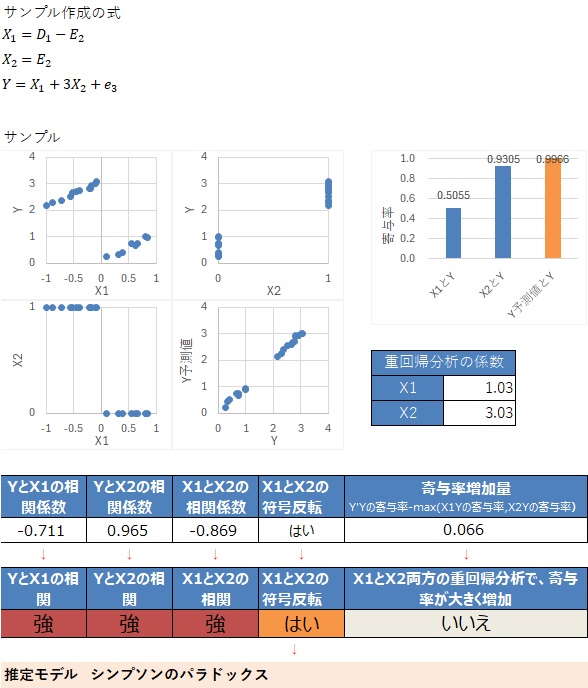
シンプソンのパラドックスに当てはまるデータの場合は、ガイドというより、グラフを見ると判断できます。
③、④、⑤、⑦は、３変数間の相関がすべて強く、シンプソンのパラドックスでもない点が共通しています。
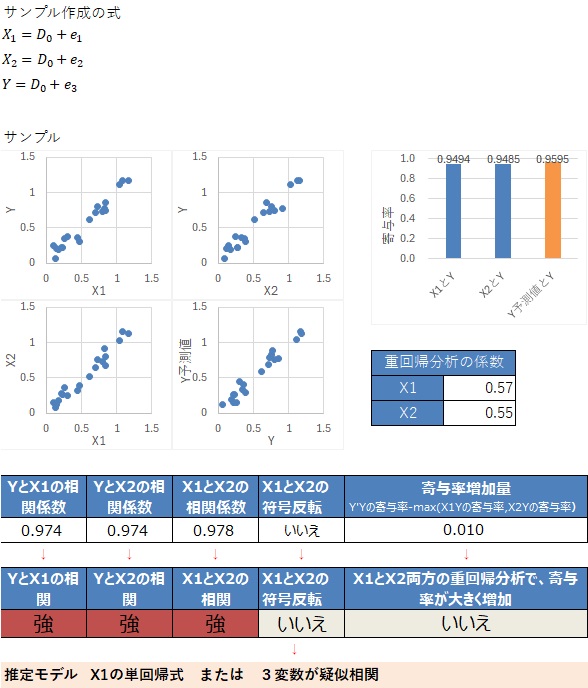
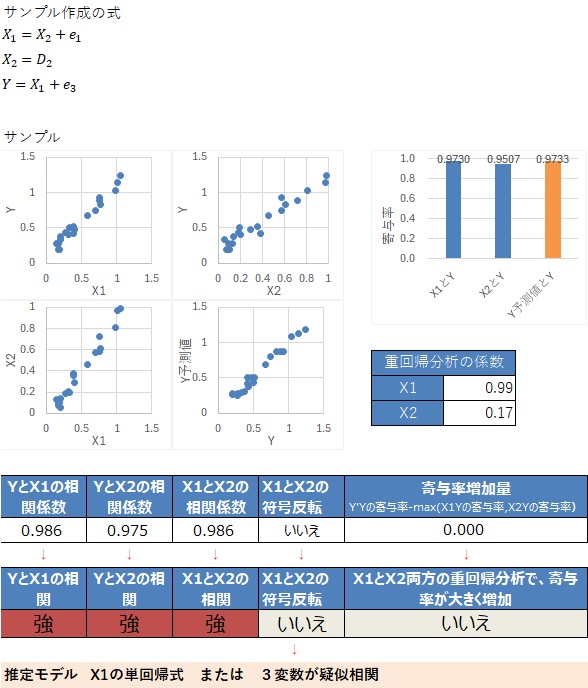
相関係数の大きさから、「X1とYに関係があり、X1とX2は疑似相関なのだろう」といった推測はできますが、データだけから、これらの４つのパターンを区別することはできないです。
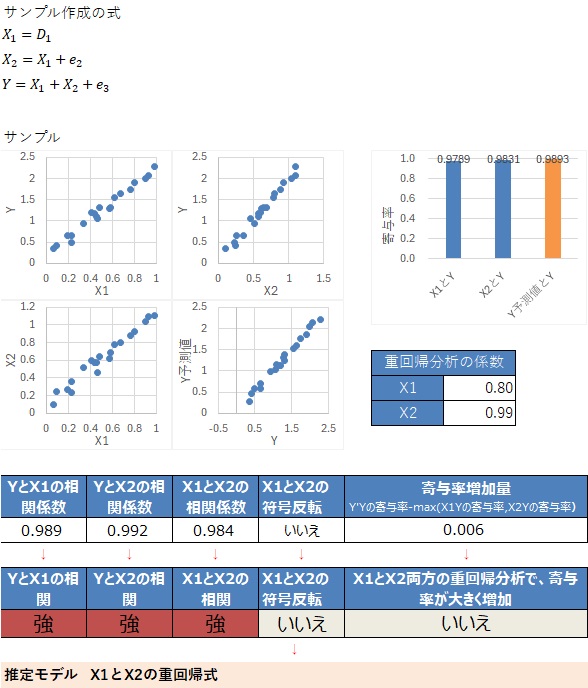
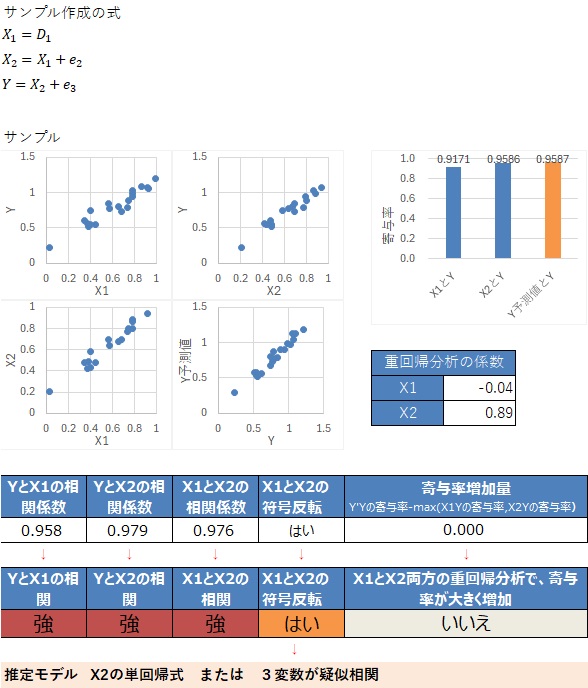
筆者の経験の範囲では、３変数の相関がすべて強い場合は、３変数が疑似相関の関係になっていることが多いです。
この例では、２つの変数を両方入れると、寄与率が大幅に増加します。
単回帰分析では、相関があるように見えにくいです。
単回帰式が正解になる例です。
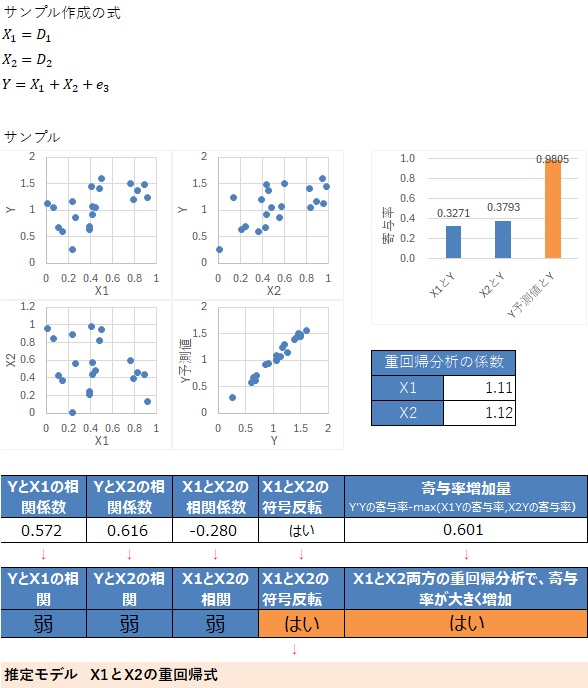
２つの変数の両方を使った方が、寄与率は高いですが、 この程度の違いでは、「１つだけの方が正解」と考えるのがポイントです。
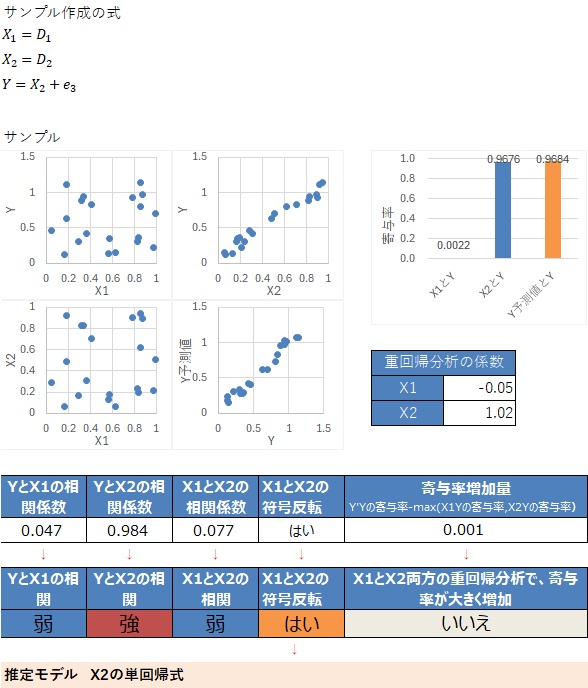
抑制変数の例です。
X1とX2の相関係数、X1の偏回帰係数、X2の偏回帰係数の３つについて、それらの積の符号の確認がポイントです。
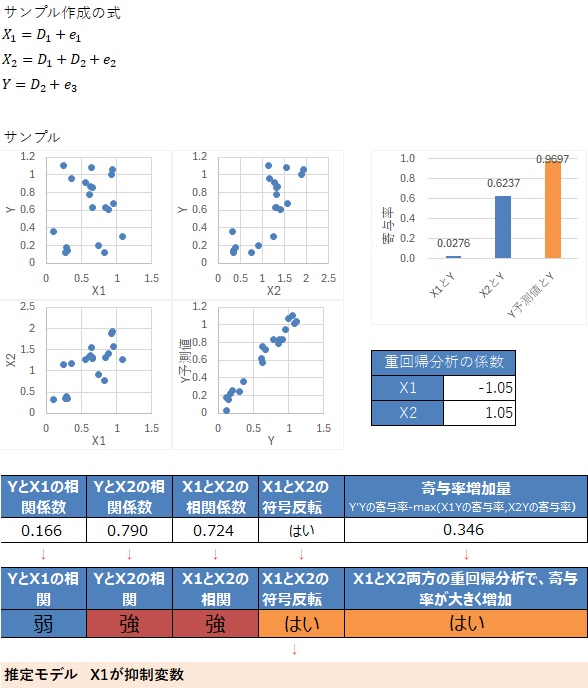
⑧と、この次の⑪では、このガイドだけでは、区別ができないことがあります。 実際のデータの背景も、考察に加える必要があります。
説明変数の差分が、重要な意味を持っている場合です。
X1とX2の相関係数、X1の偏回帰係数、X2の偏回帰係数の３つについて、それらの積の符号の確認がポイントです。
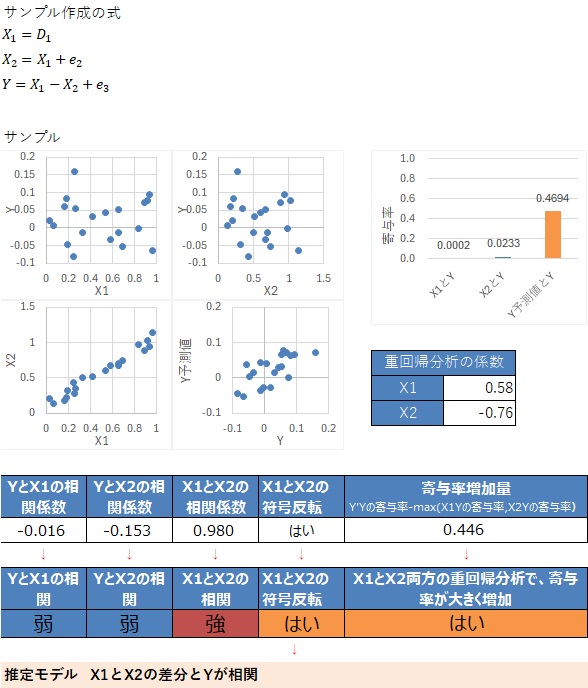
モデルの推定で誤解しやすいのは、決定係数と、検定、符号反転の使い方です。
寄与率 （決定係数）は、モデルの当てはまりの良さを表します。
寄与率には、目的変数にまったく関係のない変数だとしても、モデルに加えると、少し増加する性質があります。 そのため、少し増加する程度では、「この変数を入れた方が良い」となりません。 「少し」というのは、「0.05(5%)以下」が目安です。
上の表では「寄与率が大きく増加するか？」としています。 「大きく」というのは、「0.2（20%）以上」が目安です。
寄与率の増加量の目安については、 無関係な変数による寄与率の増加量 で詳しく説明しています。
検定 は、２つのグループの比較が有名ですが、重回帰分析の係数向けのものもあります。 重回帰分析ができるソフトウェアでは、各変数について、p値が出力されるようになっていることが多いです。
「p値が○○以下だから、この変数はモデルに入れた方が良い」という判断をしている文献が、今も多いですが、この進め方は間違いです。 p値にはサンプル数が多いだけで小さくなる性質があるため、p値の結果だけでは、確認が不足しています。
符号反転 のページがそうですが、一般的に「符号反転」と言えば、同じ変数について、単回帰分析と重回帰分析で、符号が反対になっていることを指します。 何か特別な性質のある変数のように解釈されることがあります。
しかし、 符号反転とサンプル数 のページにあるように、符号反転は、変数の選び方によっては、確率が0.5で起きるような現象です。 そのため、「符号反転」という事実に軸足を置いて、考察を進めても、実利のある考察に進まないです。
上の表の中に、同じ変数についての符号反転が入っていないのは、 符号反転とサンプル数 の結果を受けています。
上の表で、「X1とX2の符号反転」と書いているところは、具体的な確認事項は、「X1とX2の相関係数、X1の偏回帰係数、X2の偏回帰係数の積の符号がマイナスか？」です。 ①、③、⑧、②の時は、符号が決まって来るので、確認のポイントとして使えます。
上記の実施例は、Excelで作っています。 そのファイルは、リンク先にあります。
順路
次は
スパースモデリング
