トップページ | ひとつ上のページ | 目次ページ | このサイトについて | ENGLISH

符号反転

同じ変数について、 重回帰分析 と 単回帰分析 をした時で、係数の符号が反転することがあります。 単回帰分析の結果と同じ時と違う時 のページがありますが、符号反転は、その典型例です。

下の例は、符号反転の例です。 変数は、Y、X1、X2の３つです。 グラフは、YとX1、YとX2の組合せです。 X1に付いている係数ですが、YとX1だけで単回帰分析をした時が-8.1で、負（マイナス）の数です。 Y、X1、X2で重回帰分析をした時が0.23で、正（プラス）の数です。 このようにして、符号反転が起きています。

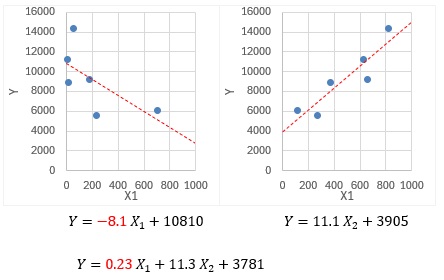
単回帰分析の結果を見ると、「X1が低い時に、Yが高い」となります。 一方、重回帰分析の結果を見ると、「X1が高い時に、Yが高い」となります。 この性質があるので、符号反転は、 統計学が生む逆説 のひとつです。

符号反転の条件式

ネットなどで見かける解説では、符号反転の原因を、「多重共線性」、「説明変数間の相関」、「抑制変数」、「シンプソンのパラドックス」などで説明することが一般的のようですが、筆者が調べたところ、符号反転が起きることと、それらの条件は無関係です。

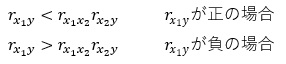
このページの結論になるのですが、符号反転は、この条件式が成り立っているデータの時に起きます。 この式の導出の仕方は、 符号反転の条件式 のページで説明しています。

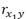
は、X1とYの相関係数です。符号反転は、X1、X2、Yの３つの変数で作られる、３つの相関係数の数値的な関係で決まります。

符号反転の条件式　その２

上の式は、もう少し踏み込むと、以下の条件も成り立っています。

この条件の時に、必ず符号反転が起きる訳ではないです。一方、符号反転が起きている時は、この条件が成り立っています。 符号反転の事例集 のページにある10のパターンでも、この条件が成り立っています。

符号反転との、向き合い方

因果関係を検証するために重回帰分析を使い、 符号反転が起きると、「因果の向きが逆になった」となって、結果の考察で混乱します。

まず、符号を根拠にして、現象を考察するのは、良くないです。 また、データの背景について、何も調べずに、単回帰分析と重回帰分析の結果だけから、因果関係を検証しようとする進め方も良くないです。

詳しくは、 符号反転とサンプル数 のページで説明していますが、「符号反転は、サンプリングによって起きる確率的な現象なので、符号反転だけを、ひとつの現象として考える必要がない」というのが、とても重要なポイントです。

順路 次は 符号反転の条件式

杉原データサイエンス事務所によるコンサルティングとセミナー