データサイエンスの道具（G7・W7・M7）

QC７つ道具・新QC７つ道具（Q7・N7）のページに、これらの道具の使いにくさ、わかりにくさも書いてあります。

それもあり、G7・W7・M7は、データサイエンスの基本的な道具として、筆者がまとめてみたものです。 G7・W7・M7のもともとのアイディアは、Q7・N7から来ています。

G7・W7はデータサイエンスの初級向け、 M7は中級向けのつもりです。
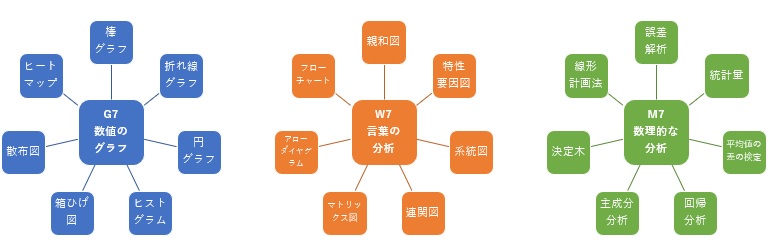
データサイエンスの道具（G7・W7・M7）

G7

G7の「G」は、「Graphs of Numbers：数値のグラフ」から取りました。 G7は、 Q7 に近いです。

G7でも、データを有効に分析するための方法として、層別はポイントです。

「層別のヒストグラムと、箱ひげ図のどちらを使うか？」、「散布図とヒートマップのどちらを使うか？」、等は、文章で説明するとなると、小難しいことになります。実際のデータに使ってみて、解析の目的や、見やすさ等で、その時その時で使い分ければ良いと思います。

W7の「W」は、「Analisis of Words：言葉の分析」から取りました。定性分析（概念分析）が多いです。概念だけの分析と、数値データも多少含む分析があります。

親和図　：　アイディアを分類する方法。ブレーンストーミングをまとめる方法。
特性要因図　：　親子関係をまとめる方法。手書きでのデータ収集の方法。
系統図（ロジックツリー）　：　系統的に分類して、具体的な内容に結びつける方法。 FMEA に似ています。特性要因図の次の段階にも使えます。
連関図　：　関係を矢印を使った図で表す。システム思考で中心的存在
マトリックス図　：　関係の度合や、優劣を、表形式にしてまとめる方法。関係の度合いは、○×の場合もあれば、点数で表現することもあります。「星取り表」とも呼ばれています。 QFD（品質機能展開）では、「二元表」と呼ばれています。
アローダイヤグラム　：　日程計画の方法
フローチャート　：　N7では「PDPC」と呼ばれます。判断を伴う計画に使われることもありますし、作業のプロセスを目に見える形にする事に使われる事もあります。

なぜなぜ分析は、いろいろな概念分析の基本になっています。

W7では、物事の階層構造（木構造）やネットワーク構造を考えます。表に出ることは少ないですが、システムの２大構造（木構造とネットワーク構造）は、G7やM7でも使います。

M7の「M」は、「Mathematical Analisis：数理的な分析」から取りました。