データサイエンス の分野で「推論」と言えば、「統計学を使った推論（統計的推論）」や「 機械学習 を使った推論（予測・推定・判定）」を指すことの方が多いので、このページのタイトルは「論理的推論」としていますが、 論理的推論が書かれている文献では、単に「推論」と書かれているのが普通です。
学問としては、統計的推論と論理的推論は別ですが、現実の場面の推論では、現実と理論の合わないところへの対策として、 両方の理論を組み合わせていくことが多いです。
現実的な推論では、「〇〇ならば××」といった論理の構造自体だけでなく、「〇〇」や「××」自体をどのように裏付けるのかも、重要になっています。 ポイントは、明確な線が引けない中で、どのように判断するのかというあたりのようです。
論理的推論の分け方には、いろいろあるようですが、ここでは演繹・帰納・アブダクション・類推にしています。
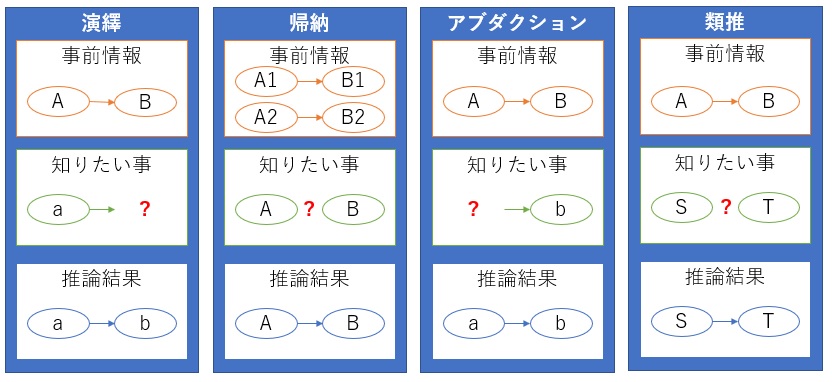
帰納法について、「演繹法ではないものが帰納法」、「前提となる根拠に含まれないものが、結論に含まれる方法」と説明している文献もあります。
このように考えると、アブダクション法や、類推法は、帰納法の一種と考えることができます。
演繹法は、前提とする法則がわからないと使えない方法です。
日常生活や社会生活の中で起きることについては、「法則」のようなものがわからないことが普通と思いますので、 そう考えると、日常生活や社会生活で起きることについて、演繹法で推論する機会は滅多にないようにも思えて来ますが、 実際は、日常的にも使われています。
私たちは、日常生活の中で無意識にたくさんの法則を使って生きています。
例えば、「雨が降ると、道路で転びやすいから、ゆっくり歩こう」といった感じの判断で使っています。
こうした法則は、自分の周辺の社会や会社でよく言われていることの場合があります。 また、こうした法則は、自分で経験的に導かれたもののことがあります。なお、この場合は、帰納法の一種でもあります。
演繹法のこのような使われ方は、時には、間違った行動にもつながります。 そうした観点で、 行動経済学 や 認知心理学 で研究がされています。 また、こうした法則の調べ方には、 応用行動分析学（ABA） があります。
演繹法は、「 記号論理学 が扱えるものが演繹法」や「数学的に厳密な扱いができる方法」と説明している文献もあります。
「定義」として、前提とする法則の正しさを宣言すれば、 記号論理学 の豊かな理論を活用することができるようになります。
これは論理的に正しい説明の方法として、数学や哲学で使われています。
数理モデリング による シミュレーション は、数理モデルの活用方法としての演繹法の使い道になります。
特に、物理学などで研究されて来た自然法則は、幅広く使える数理モデルです。 工場の中でのものづくりの理論として応用されていますので、工場の現象の推論には、 数理モデリング による シミュレーション が役に立ちます。 つまり、演繹法が役に立ちます。
論理的推論は、 定性的な仮説の探索 の方法として、使うことができます。 統計的推論は、 定量的な仮説の探索 の方法になって来ています。 推論をする時に、統計学を使う場合は、過去に何度も起きているということが前提にあります。
統計的推論を、事実の積み重ねから一般的な法則を出す使い方をする時には、帰納法の一種として使います。 アソシエーション分析 は、このような法則を見つける方法の代表的なものです。
事実の積み重ねから法則を導いて、その法則を前提にして推論して行くこともできます。 この場合は、演繹法を実施する準備のための方法として使います。
裁判の世界では、対象とする現象は１回しかありません。 その１回の情報だけで、法律にどのように当てはめるのかを決めるのは困難なため、過去の判例なども引き合いに出すようです。
現実の推論では、統計的推論と論理的推論に加えて、その中間にあるような領域の情報も使います。 条件が異なるので、「繰り返し」とは言えないものの、一部でも良いので類似点がある状況の情報や、周辺の情報も駆使して、推論します。 扱っている言葉が意味している範囲のばらつきも考慮します。 筆者の知っている分野では、 異常状態の工程解析 では、そのようになってきます。
類似の扱い方については、もう少し理論的・体系的にまとめられる良いのですが、このサイトでは、まだまとめられていません。 世の中でも、今のところ、良い資料はないようです。
「問題解決力を高める「推論」の技術 ビジネスの未来を読み解くための3つのシンプル思考」 羽田康祐 著 フォレスト出版 2020
タイトルにある「３つ」というのは、「帰納法」、「演繹法」、「アブダクション」です。
この本では、この３つについて、考え方やトレーニングの仕方を解説しています。
帰納法：共通点から結論を導く。優れた洞察を生み出す方法
演繹法：前提となるルールから結論を導く。予測と検証を可能にする方法
アブダクション：物事の表面だけでなくその背後にある法則を考え、法則から仮説を生み出す。
「ソーシャル・ビッグデータサイエンス入門 基本概念からマイニング技術,応用まで」 石川博 著 コロナ社 2014
仮説を用いないデータ解析もあるが、仮説を立てて、それを検証するアプローチがビッグデータ時代も必要としています。
仮説を立てるための推論の方法として、帰納、演繹、等の分類があります。
もっともらしい推論：演繹法と似ているが、A→Bが成り立っていて、Bが正しいことが分かった時に、Aも正しいと推論する方法。
Bが起こりにくいことであれば、あるほど、Aのもっともらしさが高くなり、その定量的な評価はベイズの定理で計算できる。
アブダクション：もっともらしい推論の考え方を使った推論法。
相関関係 ：同時に起きること（共起）として推論する方法になる
因果関係：A→B、B→Cが成り立っていても、A→Cとは必ずしも言えないことに注意が必要。
類推：ある分野で正しいことがわかっている命題を一般化して、他の分野にも適用
推移率：A→BかつB→Cの時に、A→Cを仮説とする。
「数学的推論が世界を変える 金融・ゲーム・コンピューター」 小島寛之 著 NHK出版 2012
金融や賭け事の世界で、ルールや道具を綿密に調べることによって、必ず優勢になる方法を見つけ、
それを実行することで大儲けをした数学者の例が紹介されています。
例えば、統計学の教科書では、「宝くじは、期待値を計算すると、損するようにできている。だから、宝くじを買うのは間違った行動なのだ。」、
という説明が一般的ですが、この本の例だと、期待値を計算すると得をするようになっている状況を見つけ、その状況に対して大金を投じて設ける方法が紹介されています。一見すると、ランダムや、等確率になるように作られているルールや道具について、そうではない場合を見つけるのがポイントのようです。
このような必勝法を見つけるのに数学的推論が使われているそうです。
数学的推論というのは、演繹的推論と、その応用になっている
ゲーム理論
でした。
この本は、数学的推論が役に立つことを紹介しつつ、
論理学
の入門書にもなっています。
「知覚・認知モデル論」 渡辺利夫 著 ナカニシヤ出版 2009
推論は、帰納的推論と演繹的推論、三段論法は、仮言的三段論法と定言的三段論法を、それぞれ挙げています。
「いちばんやさしい機械学習プロジェクトの教本 人気講師が教える仕事にAIを導入する方法」 韮原祐介 著 インプレス 2018
通常（従来）のシステムは演繹的。機械学習のシステムは帰納的であり、データから推論して結論を出す。
機械学習のシステムを作るには、質の良いデータが大量に必要。そのため、実際のデータを使ったテストが大事。
「信頼性の高い推論 帰納と統計的学習理論」 ギルバート・ハーマン、サンジェーヴ・クルカルニ 著 勁草書房 2009
理論には、帰納と演繹があるが、推論に使えるのは帰納。
演繹は、真実を表す表現にはなる。
帰納をする時には、「推論の信頼性」を考える必要があり、これを考える時に統計的学習理論の仕組みが参考になる。
統計的学習理論では、ばらつきを持ったデータに対して、適切なモデルを作ることで、推定ということができるようにしている。
なお、この本の内容は、言語による推論と、統計的な推論を扱っているのですが、参照しながら並走している感じです。
もしも、言語自体にあいまいさがあり、それを統計的に扱うのなら、この本の内容は、
現象学
や
認知言語学
につながるようなものになりそうですが、そこまでの話は意図していないようでした。
「なぜこれまでからこれからがわかるのか デイヴィッド・ヒュームと哲学する」 成田正人 著 青土社 2022
帰納、推論、印象、経験、未来といったキーワードについて、ヒュームの説を参照しながら、それらの意味や関係を考察している感じの本でした。
「新・論理考究 論理がはじめてわかる」 本橋信義 著 幻冬舎メディアコンサルティング 2016
この本では、「日常論理」というものが紹介されています。
ややこしいのですが、概ね以下のようなことが著者の説明のようです。
メタ推論 ： 抽象的や一般的なことを根拠として、具体的な事実の推論（例：A → B）に使われる推論。
ここで使われる抽象的・一般的なことは、その人の共同体では共通の知識として使えるもの。
メタ推論の根拠は、無意識なことが使われることもある。
演繹的推論 ： メタ推論の一種。一般法則から個別事実を導く方法
日常論理（メタ論理） ： メタ推論を含んでいる論理
数理論理 ： メタ推論を含まない論理。一般的な数学の証明は、数理論理でできている。数学の証明は、一般法則から個別法則を導いているだけではないので、演繹的推論ではない。
「ならば」という言葉には、３つの使い方があるが、混同されている。
「考えることの科学 推論の認知心理学への招待」 市川伸一 著 中央公論社 1997
論理的な推論や統計的な推論は規範的な推論としています。
日常的な推論は、記述的な推論で、
スキーマ
を使って行われていることを説明しています。
「知識と推論」 森下真一 著 共立出版 1994
論理の記号が多用されていて、難解な本です。
自動で証明するためのソフトを作ろうとして、数理論理学をコンピュータ上に実装するのは単純な作業ではなく、
計算の効率化の理論が新たに必要になるそうです。
また、論理的な部分（How）はソフトがやってくれて、人間は何（What）だけに注力することができるプログラミング言語として、
Prologを紹介しています。
「AI時代の法学入門 学際的アプローチ」 太田勝造 編著 弘文堂 2020
裁判では、法に当てはまるかどうかを判断して、当てはまれば、法が定めることを進める。
法に当てはまるかどうかの判断は簡単ではなく、ベイズ論による確率を使って判断が必要なこともある。
判断に使うのは、頻度論的な確率ではなく、ベイズ論的な確率。
帰納的論証では、飛躍がある。
飛躍とは、根拠と主張の間にあるつながりの距離。
飛躍がまったくない論証は、論証することに利点がない。
一方、飛躍があり過ぎると、誰にも信じてもらえない。
帰納的論証で有名なのが、トウールミンの論証モデル。
科学では、原因から結果を探るアプローチができるが、法の世界では実験はできないので、結果から原因を探る方法になる。
PROLOGは、論理型のプログラミングができるので法律のエキスパートシステムに向いている。
法律の専門家に扱いやすいものではないので、PROLEGが開発されているが、PROLEGでは論理式で入力する必要があるため、
著者は自然言語からシステムを作る方法を開発中。
「要件事実・事実認定入門 裁判官の判断の仕方を考える」 伊藤滋夫 著 有斐閣 2005
同じ裁判でも、民事と刑事では考え方が違うそうで、この本は民事を扱っています。
副題にもありますが、裁判官はどのように考えるのか、という視点でまとめられています。
「法律人工知能 法的知識の解明と法的推論の実現」 吉野一 編者 創成社 2000
国連売買条約を例にして、法律のエキスパートシステムの作り方を説明しています。
法律の中にある論理構造を人が全部読み取って、プログラミング言語に翻訳する作業があります。
順路
次は
「ならば」や「だから」の多義性
