論理学的には、「Aは、Bに含まれる」と「Bは、Cに含まれる」と言う内容があれば、「Aは、Cに含まれる」となります。
論理的な説明や、合理的な判断でないことに対しての批判は、会議の中や、ニュースの中などでよく見聞きします。
しかし、 行動経済学 では、一見、合理的な判断が、実は間違っていることの例が研究されています。 また、 リスクコミュニケーション は、"その人にとっては"合理的な事実のぶつかり合いを、どのようにしてまとめるのかがポイントになります。
論理学の歴史は古く、その知識は、議論や論述で重要です。 データサイエンス の分野では、 因果推論 や プログラミング を正しく行うための理論になりますし、 人工知能 の理論にもなります。
論理学では、理屈が正しいかを重視しますので、現実に正しいかどうかとは無関係に理屈が進むことがあります。 それが、パラドックスや論争の種になると同時に、"正しい理屈"の研究を発展させて来たようです。
言語による論理を扱うのが形式論理学です。 アリストテレスなど、かなり昔の人からの歴史があります。
記号論理学では、形式論理学が記号で表せます。 「記号を使う」という発明により、論理学はシンプル、かつ、体系的にまとめられるようになりました。 ただし、記号だけの話は抽象的なので、一般人にはとてもわかりにくい世界です。
古典論理学は、「〇ならば×」、というように、はっきりとした２つの物の関係を表すようになっています。
現代では、あいまいなものや、複雑なものを扱う話も出て来ています。
論理学の解説では、言葉や記号の操作だけで、議論が進みます。 この操作は、疑う余地がないのですが、この操作を現実に起こっていることの考察や議論で使おうとすると、うまく行かないです。
論理学的に完璧な思考を絶対視して、そうではない思考をレベルが低いような言われ方がすることもありますが、 論理学的に完璧な論理的推論というのは、理想でしかないように筆者は考えています。
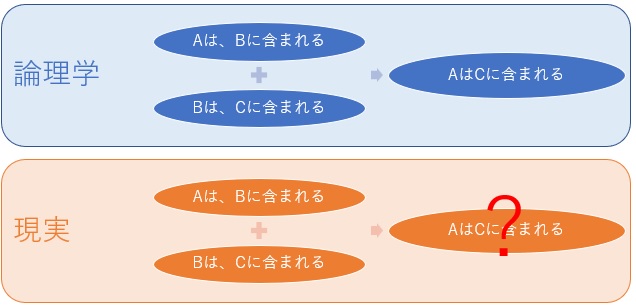
論理学的には、「Aは、Bに含まれる」と「Bは、Cに含まれる」と言う内容があれば、「Aは、Cに含まれる」となります。
ところが、現実的な場面では、 「Aは、Bに含まれる」と「Bは、Cに含まれる」だとしても、「Aは、Cに含まれない」ということが起きます。 こういうことが起きる原因としては、例えば、「B」が同じものではない場合があります。 また、「含まれる」の意味が違う場合も考えられます。
論理学では、「B」と書けば「B」なのですが、現実的には「B」と呼ばれる何かがあり、その「何か」と「B」は同じではありません。 こういう話は、 記号学 や 認知言語学 の中であります。
「論理学超入門」 グレアム・プリースト 著 岩波書店 2019
妥当性、真理関数、名前と量化表現、記述と存在、自己言及、必然性と可能性、条件文、未来と過去、同一性と変化、曖昧さ、確率、逆確率、意思決定理論、
チューリングとアルゴリズム、ゲーデルの不完全性定理、という構成で、論理学を俯瞰しています。
論理学の歴史の解説もあります。
確率を計算して、確率の高い方を選択する話や、期待値が高いものを合理的判断とする
統計的な意思決定
の話もあり、一般的な論理学の解説にはない内容が入っています。
「論理学 考える技術の初歩」 エティエンヌ・ボノ・ド・コンディヤック 著 山口裕之 訳 講談社 2016
1780年にポーランドで初版が発行された本の、訳本です。
かなり古い本です。
最近の分類だと、「論理学」と言うよりも、「科学哲学」の方が良いかもしれません。
人間は自然から、その理（ことわり）を学ぶ存在である。
学び方は、分析。
分析は、分解と再構成。
分析を表す方法が言語なので、言語の使い道が大事。
この本を読むと、最近の分類で論理学と言われる学問は、
言語の中にある理について、初歩的なものから始まり、高度なものを究めてきた学問のように思えて来ました。
「論理学をつくる」 戸田山和久 著 名古屋大学出版会 2000
古典論理では、真と偽の２値を扱う。
これでは未来のことも、すでに決まっているような話しかできない。
非古典論理は、この限界を超えるもの。
多値論理・ファジー論理：真理値が３つ以上ある。排中律を捨てることができる。
直感主義論理：数学では直感主義でも証明が行われるので、その直感主義の論理を取り出したもの。
排中律の無制限な適用を制限する。
様相論理：古典論理に、可能性と必然性の演算子を加えたもの。
「論理学講義 真に思惟することへの手引き」 村上恭一 著 成文堂 1986
形式論理学の歴史の本です。
カントやヘーゲルの弁証法が最後に来ます。
「例解・論理学入門」 弓削隆一・佐々木昭則 著 ミネルヴァ書房 2009
「議論」にも役立つ、論理学の本を目指して作られています。学生向けに、論文や採用面接での論理の作り方も解説しています。
命題論理：接続詞で作られる論理
述語論理：「すべて」と「ある」で作られる論理
演繹的な推論は絶対確実。しかし、前提が間違っていれば、推論も間違ったものになる。
日常の議論では、前提が省略されるのが普通。
前提を詳細に書き出すのは時間の無駄になるし、注目すべきところがわかりにくくなるので、省略は悪いことではない。
議論は、主張と根拠でできている。
議論の正しさを確認するには、根拠の正しさと、主張への反例の確認をする。
反論をただ受け入れたら、議論にならない。
反論と再反論を重ねることで、議論は厚みを増す。
主張の内容だけだと、相手はイメージできないので、「例えば」で始めて具体的なエピソードで補足する。
「本当にわかる論理学」 三浦俊彦 著 日本実業出版社 2010
「権威を一緒に見せることで、主張が正しいように見せたり、誹謗を一緒に見せることで、主張が間違いのように見せる論法がある。」、
といったように、論理的な思考にまつわる様々な事に触れています。
「計算の順番を工夫すると、計算が劇的に簡単になる」といったことが、数学ではありますが、
そのようにして、どうしてそのような発想をしたのかはわからないけれども、アイディアとしては素晴らしいものを、「直観」や「ヒューリスティクス」と呼んでいます。
「発想のための論理思考術」 野内良三 著 日本放送出版協会 2010
・説得は詭弁。しかし、生産的な議論が、論理的であることは少ない。
・三段論法は、論証に使うこともできる。
新しい発想に結び付けるための方法に使うこともできる。ただし、結論をどのようにでもできてしまう使い方ができる点は問題。
・論理の正しさの確認には、ベン図や、有向グラフも使う。
「知識と推論」 新田克己 著 サイエンス社 2002
さまざまな推論法が、コンパクトかつ体系的にまとまっています。
「真（しん）」と「偽（ぎ）」の２値の論理の議論の中では、
真偽が場合や状況によって変わる論理を扱うための、「様相論理」というのが、興味深いものでした。
人工知能
との関係がよく書かれています。
応用例として、法律の分野での推論が解説されています。
「図解雑学 論理学」 平尾始 著 ナツメ社 2005
記号論理学の記号の意味や使い道を解説しています。
見開き2ページで話題が完結するようにして、しかもそれぞれの話題はクイズ形式になっていて、読者に考えさせるようになっています。
・記号論理学は、0と1だけでできている。あいまいさはない。0と1だけで数学の計算もできるようになる。
・二重否定は、日常用語としては、否定前の文と異なる意味を持つが、論理学では、否定前と同じになる。
「思考の回路 論理学ABC」 平野耿 編 富士書店 1995
形式論理学、記号論理学、弁証法、と続きます。
言語の構造の本のような印象です。
「逆説論理学」 野崎昭弘 著 中央公論社 1980
論理の中でも、逆説を扱っています。
いろいろな逆説が出て来ます。
「「論理」を分析する」 八木沢敬 著 岩波書店 2018
論理を中心において、心理など、論理の周辺にあるものと比べながら、論理を説明しています。
「数学的推論が世界を変える 金融・ゲーム・コンピューター」 小島寛之 著 NHK出版 2012
記号論理学の入門書としての側面もあるのですが、自分が有利になるために記号論理学を使うという話を絡めた内容になっています。
ゲーデルの不完全性定理も丁寧に解説されています。
「まったくゼロからの論理学」 野矢茂樹 著 岩波書店 2020
前半は、言葉で論理学を説明し、後半は、それを記号を使って説明しています。
「文系のための記号論理入門 命題論理から不完全性定理まで」 金子裕介 著 朝倉書店 2021
記号論理を体系的に説明しています。
「現代数理論理学序説」 古森雄一・小野寛晰 著 日本評論社 2010
数学の本のように、定義と定理を順に説明するきちんと説明する形で書かれています。
命題論理、述語論理、いろいろな論理（非標準論理）の順になっています。
「現代論理学」 安井邦夫 著 世界思想社 1991
記号を中心とした書き方で、命題論理学と述語倫理学、不完全性理論と進みます。
数学の記述のための論理学が意識されていて、応用していく数学の理論としては自然数論が紹介されています。
「情報科学における論理」 小野寛晰 著 日本評論社 1994
記号を中心とした書き方で、命題論理、述語論理、様相論理、直感主義論理、自然演繹、と続きます。
「機械学習」 Peter Flash 著 竹村彰通 監訳 朝倉書店 2017
論理モデル：
決定木
を使って、データの重複を避けて、現象の論理的な構造を見つけるものを概念学習。
アソシエーション分析
を使って、データの重複を許して、現象の論理的な構造を見つけるものがルールモデル。
「認識論と論理学 問答法から帰納法へ」 高崎直道 監修 春秋社 2012
論理学はこの本の中のひとつの章で、他の章は、存在論、認識論、真理論、輪廻、といった仏教の話題です。
論理学の章の中では、３段論法も出て来るのですが、「因果関係はあるのか？ないのか？」、という問いに対しての、仏教での考え方を示しているようでした。
「インド人の論理学 問答法から帰納法へ」 桂紹隆 著 中央公論社 1998
インド人には、帰納法を使って論理的に考える習慣が昔からあるそうです。
インド人の論理学だけでなく、近代の政治や文化の話題もたくさん取り上げられています。
順路
次は
品質学
