次は
質的比較分析（QCA）
ラフ集合分析は、物事をラフに理解するための方法です。 「特徴を見つける方法」とも言えます。
データ全体を眺めるための方法ではなく、部分を抜き出す方法なので、 データマイニング の一種です。
「ラフ集合」という集合の話と、ラフ集合を見つけるための計算方法は、一対一の関係ではないです。 ラフ集合を見つけるための計算方法は、 デザイン や企画のための手法として、 感性工学 の分野で精力的に研究されています。 このページでは、感性工学の分野で使われている計算方法を、「ラフ集合分析」と呼んで、まとめることにしています。
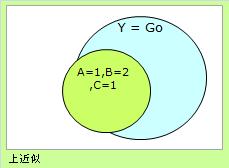
ラフ集合のYは、「合格」「不合格」のような、質的データです。 ここでは、Xを質的データとして説明しますが、応用として量的データも使えます。
例えば、Xの変数として、A、B、C、D、E、Fの5つがあって、それぞれに「1」と「2」という、 2つのカテゴリーがあるとします。
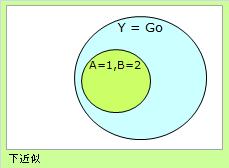
Yが「合格」の中に、「A=1、B=2」が、必ず含まれているのなら、 「合格」の下近似は、「A=1、B=2」になります。
「合格」の中に、「A=1、B=2、C=1」が、必ずではないけれども、含まれていることが多いのでしたら、 「合格」の上近似は、「A=1、B=2、C=1」になります。
下近似や上近似になるXの水準の組合せは、ひとつとは限りません。 複数見つかるので、「複数の成功パターンを見つける」、といったことに使えます。
上記で、「Xは量的データでも使える」、と書きましたが、ラフ集合分析では、 「あり」と「なし」や、「暑い」と「寒い」のように、両極端の概念を、0から1の間の連続量で表しているデータを対象にしています。 このようなデータとして、 SD法 のデータがあります。 ラフ集合分析は、 アンケート の分析に適しています。
下近似は、「データから、確実に言えること」なので、使われることが多いようです。 以下は、下近似の見つけ方ですが、上近似の場合も大きくは変わりません。
ラフ集合分析の面白いところは、それぞれのYに対して、下近似が独立して求まるところです。 例えば、Yが合格の下近似が「A=1、B=2」の時に、 不合格の下近似が「A=2、B=1」と言う風に、逆が求まるとは限りません。
Xが量的データの場合、2.の段階の「異なっている」というのは、差の大きさで判断します。
ラフ集合分析と アソシエーション分析 には、密接な関係があります。
上記の下近似は、アソシエーション分析でいうなら、
P( "Y = GO" | "A = 1 and B = 2") = 1
として、確信度で表せます。
上近似も、
1 > P( "Y = GO" | "A = 1 and B = 2") > 0
として、確信度で表せます。
アソシエーション分析 にあるRの実行例では、3つ以上の質的変数の組み合わせを探さないために、「maxlen = 2」としていますが、 これを３以上にすると、上記のように "A = 1 and B = 2"といったものも見つけられるようになります。
「人の考え方に最も近いデータ解析法 ラフ集合が意思決定を支援する」 森典彦・森田小百合 著 海文堂 2013
私たちは、「要するにこういうこと」、という風に物事を理解することがあります。
そのように理解するためのプロセスが、ラフ集合で説明できるため、「人の考え方に最も近いデータ解析法」というタイトルになっています。
扱っている事例は、車のデザインのような感性工学関係のものだけでなく、成績が伸びない子供の分析や、
市街地の活性化（
まちづくり
）の話題もあります。
デザインの指針としては、分析によって特徴を見つけ、特徴に合わせたデザインをしたとしても、
結局は誰の好みにも合わないものになりかねない。
あいまいな部分に新規性を探る余地があるそうです。
データのサンプルが多い場合の前処理として、
クラスター分析
や
数量化Ⅲ類
による、サンプルのグループ化を紹介しています。
属性値は、グループの平均値を使います。
連鎖構造についての、コメントが示唆に富んでいました。
・抽出したルールの和集合は、連鎖構造を持つ。
・人の好みは、連鎖構造を持つから、
アンケート
で、ひとつの好みを選ばせるのは、無理を強いている評価になる。
・ひとつの言葉には、多様な意味がある。
意味は、その言葉の使われ方で決まる。
つまり、言葉も連鎖構造を持っている。
・グループ全体に共通した概念がなくても、個々の具体的な意味が連鎖的につながっていれば、
全体としてまとまった意味を持つ。
このような形で会社の
デザイン
のイメージを作っているなら、高度なデザイン管理をしていると言える。
・
判別分析
や
数量化Ⅱ類
はラフ集合による分析と扱うデータの形が同じだが、平均的な特徴を見ている点が、ラフ集合による分析と異なる。
「ソフトコンピューティングのロジック 「人間の立場」で情報を扱う情報処理技術」 赤間世紀・宮本定明 著 工学社 2008
論理を扱う手法を紹介している本です。
（記号論理学の書き方なので、筆者には難解でした。）
古典的な２値の論理から始まって、あいまいな情報を記述するためのロジックとして、
ファジィ理論、
荒い情報を記述するためのロジックとして、ラフ集合が紹介されています。
「「ラフ集合理論」入門 “粗い情報”の理論と推論への応用」 赤間世紀 著 工学社 2019
２冊に分かれています。
この本も
記号論理学
の書き方です。
「ラフ集合と感性 データからの知識獲得と推論」 森典彦・田中英夫・井上勝雄 編 海文堂 2004
ラフ集合は、ラフに記述して特徴をつかむための方法、としています。
計算が詳しい本です。
「数理的感性工学の基礎：感性商品開発へのアプローチ」 長沢伸也 ・神田太樹 編 海文堂 2010
感性を分析する方法のひとつとして、ラフ集合が簡単に紹介されています。
ラフ集合は、縮約によって、行列形式の水準データの特徴を得る。
「商品開発と感性」 長町三生 編 海文堂 2005
9章がラフ集合で、感性のあいまい性と、非線形性を扱う手法とされていました。
「ラフ集合の感性工学への応用」 井上勝雄 編 海文堂 2009
デザインの企画、システム開発等への、応用の事例集です。
順路
次は
質的比較分析（QCA）
