システムズエンジニアリング の中では、システムを設計したり、システムを評価したりする時に、様々な数理モデルや論理モデルが役に立ちます。 その中でも特に重要なのが、システムを表現したり、システムの機能の一部になるモデルです。
簡単な例では、「XとYには関係があるシステム」、「XをYに変換するシステム」と表現していたものが、数理モデルを使うと、
Y = 2 X + 3
と表現できます。
システムの構造モデル を考えた後に、多少、高度なシステムの振る舞いを表そうとすると、数理モデルや論理モデルが必要になります。
システムの数理モデルや論理モデルは、いくつかの分け方があります。
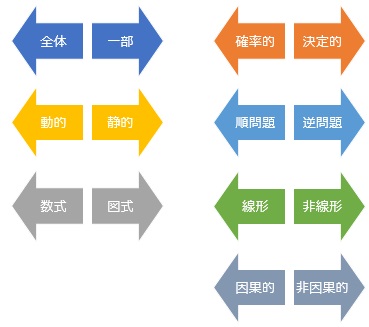
システム全体を表しているモデルと、システムの一部を表しているモデルがあります。
全体を表すものとしては、例えば、自然科学や社会科学で、〇〇の方程式のようなものがあります。
一部を表すものとしては、上記の、
Y = 2 X + 3
のように、単純な数式で表せるものは、身近なところにいろいろあります。
システムの機能の数理モデルには、数式で表せるものと、図で表せるものがあります。
数式で表せるモデルでは、〇〇方程式というような数学で表現できるものです。
図で表せるモデルは、図の一部について、確率（比率）、行列といった数学や、 論理学の表現を使います。
静的というのは、系が時間によって変化しないことを言います。 定常的とも言います。
「ダイナミックモデル」というのがありますが、これは動的モデルのことです。 よくある動的モデルは、時間に関する常微分方程式や差分方程式になっています。 時間変化を、微分や差分で表現します。
動的システムは、制御系のシステムの理論としての歴史があり、 制御工学 として発展しています。 制御工学では、動的線形システムが中心です。
動的非線形システムは、 カオス の分野のテーマでもあります。
静的システムの学問は、 回帰分析 が代表的です。
品質工学 で 「機能性」 という言葉を使って評価しようとしているのは、静的線形システムです。
確率論モデルと決定論モデル という違いもあります。
いずれも数式を使うモデルですが、確率論モデルは、図式で表しているモデルが、「必ずこうなる」という訳ではないことを表現するのにも使えます。
順問題と逆問題 というのは、システムのモデルの使い方の違いになります。 どちらの問題と考えているのかで、モデルのタイプが違って来ます。
順問題のアプローチに使われることが多いのは、 自然科学や社会科学の分野で発見されて来たモデルです。 逆問題のアプローチに使われることが多いのが 統計モデル です。
「線形 か非線形か」というのは、システムが数式で表される時の区別の方法です。
Y = a * X
という式があったとします。
因果的モデルでは、Xを入力、Yを出力とします。
非因果的モデルでは、XとYは、この式を介して同時に成立している値として解釈します。
データサイエンス は、元々、 統計学 を専門にしている方々から生まれて来た分野なので、2022年の時点でも、統計学を中心とした体系で語られるのが一般的です。
しかし、統計学は万能ではなく、例えば、 現実と統計モデルとのギャップ があります。 これが原因で、 AIプロジェクト、機械学習プロジェクト、データ分析プロジェクトといった プロジェクト が、挫折したりもします。
こういったプロジェクトでは、システムを作ろうとします。 システムを作るのなら、その核になる数理モデルは、上記のような視点で、幅広く考えると良いです。 従来、 データサイエンス や 人工知能（AI） と言われていた手法は、この中の一部という位置付けになります。 （たいていは、自分にとって専門外の分野の知識が必要になるので、筆者自身もうまく進められている訳ではないですのですが。。。）
プロセスシステム工学は、化学系の工場を研究の対象にすることが多いようですが、 どんな工場でも使えそうな内容もあります。 工場という大きなシステムに対して、いろんなデータサイエンスを持ち込みます。
下記は、システムそのものや、システムの一部の機能を表現する数理モデルの解説が詳しい本です。 システムズエンジニアリング のページにも「システム工学」がタイトルになっている参考文献がありますが、それらの本の中にも同じような内容が含まれていることがあります。
「システム理論 I」 大橋弘忠・鳥海不二夫・白山晋 著 丸善出版 2015
システムの概論の後に、動力学系モデル。
「システム理論 II」 大橋弘忠・鳥海不二夫・白山晋 著 丸善出版 2016
離散モデル（オートマトン）、ネットワーク、確率モデル（確率過程）で構成。
「現代システム科学概論 システム思考を支える知の基盤」 木村英紀 著 東京大学出版会 2021
システム科学の歴史の説明の後に、各論になります。
各論は、最適化、モデリング（回帰、状態空間、等）、学習（ニューラルネットワーク、強化学習、等）、状態推定と予測（カルマンフィルタ、粒子フィルタ）、制御。
「経営のためのシステム工学」 西川智登・清水静江 著 朝倉書店 1990
いろいろなシステムの概観・回帰分析・状態方程式・数理計画法
「次世代の化学プラント プロセスシステム工学入門」 梅田富雄 編著 培風館 1995
「コンピュータを使って、最適な生産ができて、安全や環境に配慮している化学プラントを作りましょう。」、
という主旨の、啓蒙的なことが書いてある本です。
「プロセスシステム工学」 松山久義 他 著 オーム社 1992
数値計算、
数理計画法
（生産管理や、プロセス設計の方法として）、
モデル予測制御（
古典的制御工学
のPID制御より高度なもの）、
パターン認識
(異常の解析として）が解説されています。
「知的プロセスシステム」 化学工学会 編 槙書店 1993
事例集や、論文集という感じです。
内容は制御系を中心に、多岐にわたっています。
エキスパートシステム
によるプロセスの設計や制御、
ファジィ理論
による制御、
ニューラルネットワーク
による制御、
ペトリネット、
遺伝的アルゴリズム
によるスケジューリング問題、
感性情報処理、
ブラウン動力学（粒子系のシミュレーション）
順路
次は
制御工学
