高次元を２次元に圧縮して可視化 と クラスター分析 の２つは サンプルの類似度の分析 の代表的なものです。
このページの次元削減クラスタリング分析というのは、両方の合わせ技です。
ベクトル量子化は、 ベクトル量子化平均法 、 ベクトル量子化回帰分析 、 ベクトル量子化ロジスティック回帰分析 に応用できるのですが、「作ったクラスターが、どのようなものかがわからない。」、という説明可能性の面での弱点があります。
これらの方法の前に、次元削減クラスタリング分析をすると、説明可能性が改善します。 また、「クラスターの数は何個が良いのか？」ということを調べる方法にもなります。
手順は、下記の３段階です。
まず、
高次元を２次元に圧縮して可視化
です。
２次元データにしてしまいます。
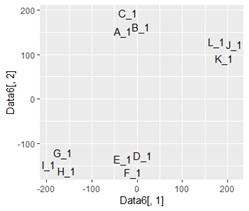
「サンプルA、B、Cは同じグループ」といった分析は、これでできます。
グループに分かれることはわかるのですが、「グループのそれぞれの特徴は？」ということは２次元データを見てもわかりません。
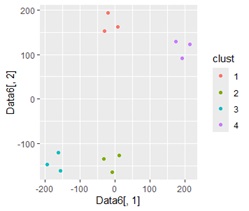
次が、 ２次元散布図を使ったクラスター分析 です。 ２次元散布図で確認できるので、クラスタリングの出来栄えや、どのような形のクラスターなのかが分析できます。
この段階では、「グループに分かれる」という目で見て分かることを、色付けすることまでができます。
クラスタリングの原因分析 ラベル分類 の手法なら、決定木以外でも使えなくはないのですが、決定木には、 「目的変数が質的変数で、しかも、多クラスでも良い」、「分析結果の説明性がある」という特徴があるので、このアプローチには便利です。
クラスター分析の結果（クラスターの番号等）を目的変数にして、 クラスター分析で使ったデータを説明変数にして、 決定木 を実行します。
すると、クラスターがどのように分けられているのかが、決定木の結果からわかります。
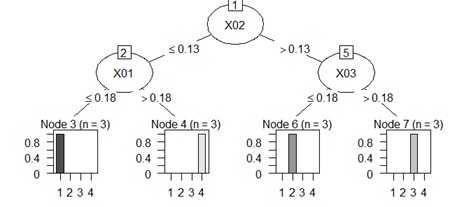
Rによる実施例は、 Rによる次元削減クラスタリング分析 のページにあります。
R-EDA1
では、次元圧縮を選んでから、クラスタリングにチェックを入れると、決定木分析まで出て来ます。
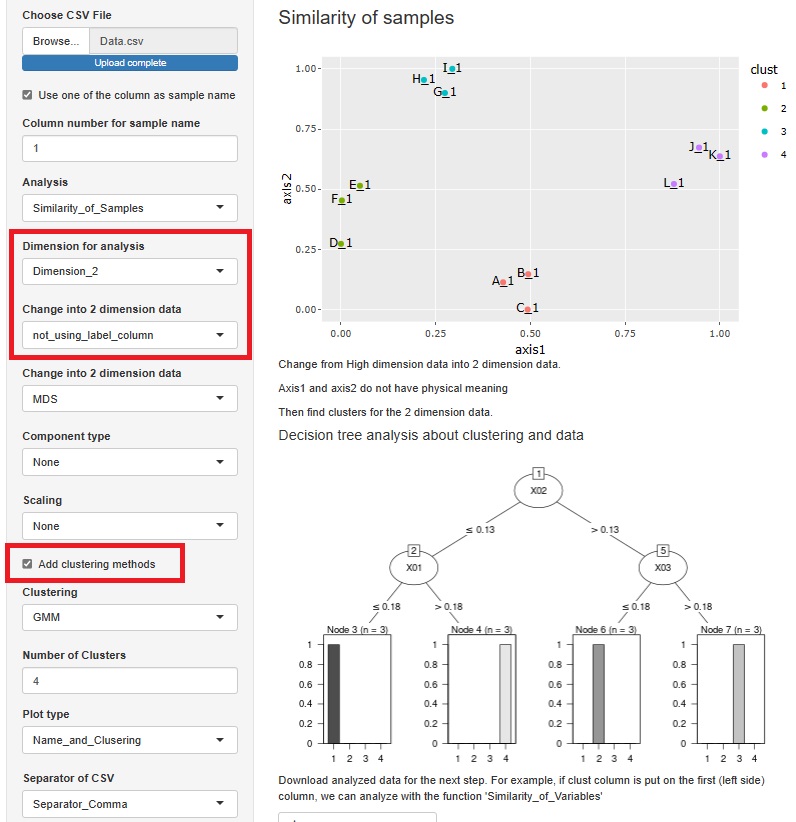
順路
次は
クラスター分析による外れ値の検出
