 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
 トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
トップページ |
ひとつ上のページ |
目次ページ |
このサイトについて | ENGLISH
尤度の比は、 尤度の活用 のひとつです。
このページでは、尤度の比を対象とするデータ分析(尤度比分析)を説明します。 、 尤度比検定 や ベイズファクター は、このページの内容の応用です。
なお、このページは、 尤度比検定 や ベイズファクター とは、どういうものなのかについて、筆者が改めて整理する中でまとめたものです。 尤度比検定 や ベイズファクター を理解しやすく、また、現実の具体的な問題に活用しやすいようにまとめてみました。
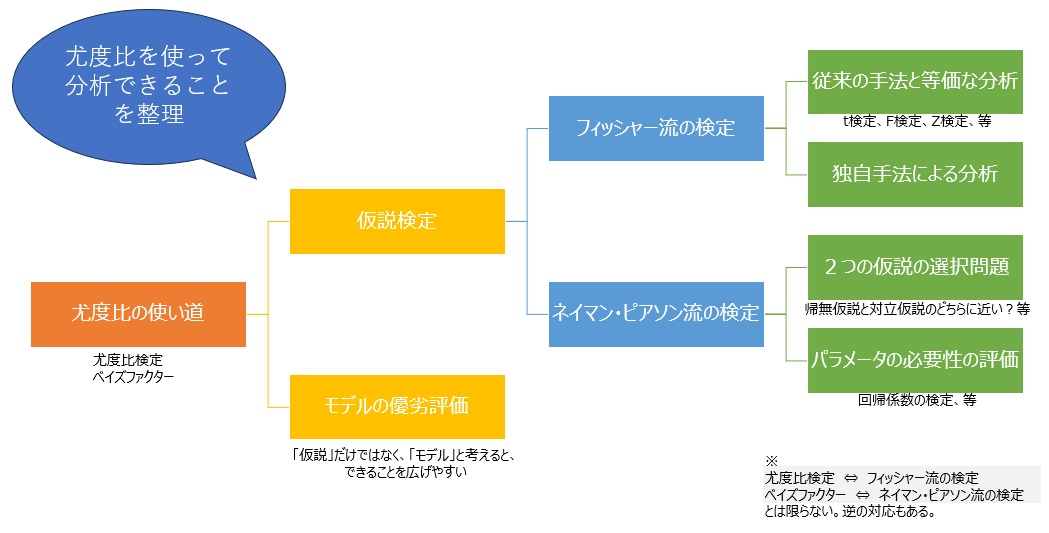
2種類の対立仮説 のページにあるように、対立仮説の考え方で大きく分けると、フィッシャー流とネイマン・ピアソン流の2種類があります。
尤度比はどちらの検定でも使えますが、使い方が違います。
フィッシャー流の仮説検定に尤度を使う場合は、尤度比検定では、帰無仮説が分子です。
1よりも小さければ、「帰無仮説ではない確率の方が高い」という意味になります。 ほぼ1の場合、「帰無仮説と、データには違いがない」という意味になります。
帰無仮説と対立仮説の検定 のページにあるように、 ネイマン・ピアソン流の検定 を厳密にやろうとすると、帰無仮説と対立仮説の両方について、確認の作業が必要になります。
「どちらの仮説でもない」という可能性がない場合、別の言い方をすれば、「帰無仮説に近い・対立仮説に近い・帰無仮説と対立仮説に違いがない」の三択の場合、尤度比の値を見れば、この評価ができます。2つの仮説に対して、それぞれ確認作業をする必要がないです。
尤度比が1よりも十分に大きければ、分子の方の仮説に近いです。 1よりも十分に小さければ(ただし、0よりは大きい)、分母の方の仮説に近いです。 尤度比が、ほぼ1の場合、「両方の仮説の中間」ということになりますが、これはつまり、「仮説に違いがない」という意味になります。
分子に帰無仮説、分母に対立仮説を置く尤度比検定の使い方は、 ネイマン・ピアソンの定理により、 最強力検定 になることが知られています。
上記よりも具体的に、尤度比の計算方法を説明します。
例えば、平均値の検定で、帰無仮説が「母平均が0.5」の場合、母平均を0.5とした場合の尤度が分子になります。 母平均を、データの平均値(最尤推定値)とした場合の尤度が分母になります。
例えば、平均値の検定で、帰無仮説が「母平均が0.5」の場合、母平均を0.5とした場合の尤度が分子になります。 対立仮説が「母平均が0.7」の場合、母平均を0.7とした場合の尤度が分子になります。
上記では、「母平均が0.5」や、「母平均が0.7」という固定値(パラメータ)の場合の尤度の計算方法を例にしました。
例えば、対立仮説が「母平均は0.5ではない」という場合に、「母平均は、0から1の範囲の一様分布」と置いて、尤度を計算するする方法があります。
このように「母数は変数」とする考え方は、ベイズ統計でよく行われますが、ベイズファクターに限定されるものではないです。
ネイマン・ピアソン流の検定の使い方として、 例えば、帰無仮説が「傾きの係数なし」、対立仮説が「傾きの係数あり」とすることができます。 尤度比が1に近いということは、「傾きの係数をいれても意味がない」ということになります。
この使い方は、例えば、回帰係数の検定になります。
ところで、「帰無仮説・対立仮説」と考えるよりも、「傾きなしのモデル・傾きありのモデル」と考えると、モデルの優劣を評価する方法として、さらに応用が広がります。
例えば、「一様分布モデル・正規分布モデル」という2つのモデルについて、どちらの方がデータに合うのかを調べる方法として、尤度比分析ができます。
シンプルな尤度関数 のページの結果を使うと、正規分布を尤度関数にする場合は、以下のようにまとめられます。 結論から書くと、尤度比は分母と分子のモデルの違いだけでなく、サンプル数にも依存します。
nはサンプル数、x-barは平均値、σ-barは標本分散の平方根です。
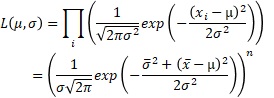
これを使うと、尤度比は以下のようになります。
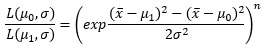
x-barが、μ0とμ1のちょうど平均値の場合は、
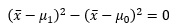
になります。つまり、尤度比は1になります。
x-barが、μ0よりもμ1に近い場合は、
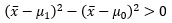
になります。これをn乗したのが尤度比なので、nが大きいと、尤度比は非常に大きな数になります。
逆に、x-barが、μ0よりもμ0に近い場合は、
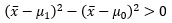
になります。これをn乗したのが尤度比なので、nが大きいと、尤度比は限りなく0に近くなります。
順路


 次は
尤度比検定
次は
尤度比検定

