例えば、サンプル数が３の時の、上の積の式は、下のようにまとめられます。x-barは、平均値です。σ-barは、標本分散の平方根です。
ベイズ統計 や 最尤推定 で「尤度」と言えば、サンプル数が１の尤度関数の積を想定することが普通のようです。
この積の式は、冗長な式になりますが、シンプルな式にまとめられることもあります。
シンプルにまとまっていると、関数の特徴がイメージしやすくなります。
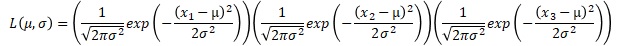
例えば、サンプル数が３の時の、上の積の式は、下のようにまとめられます。x-barは、平均値です。σ-barは、標本分散の平方根です。
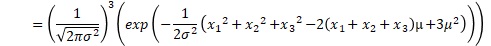
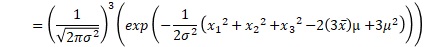
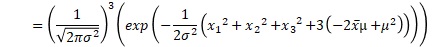
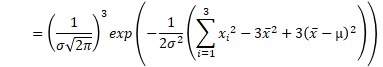
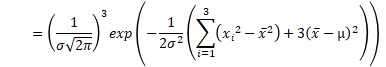
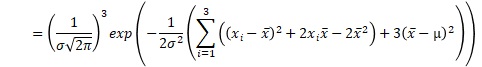
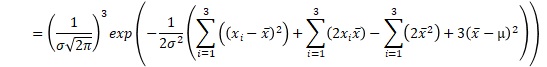
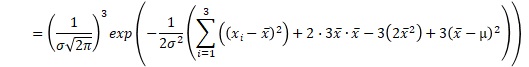
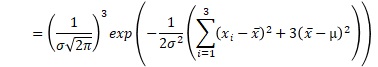
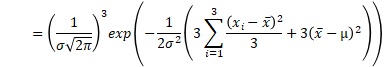
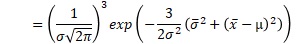
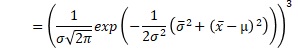
これを一般化すると、正規分布が尤度の時は、以下のようにまとめられます。nは、サンプル数です。
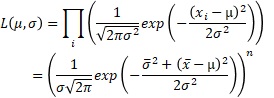
ここまで整理できていると、データセットがあった時に、サンプル数、平均、標本分散を計算すれば、任意のμとσの時の尤度が、簡単に求まります。
なお、このシンプルな式は、サンプル数が２個以上の時に使えます。 サンプル数が１の尤度関数 は、標本分散が計算できないので、当てはまらないです。
対数尤度にすると、もっと見通しが良くなるようです。
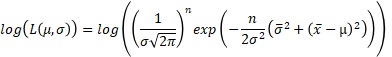
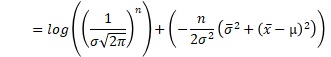
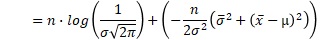
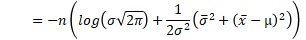
ところで、 サンプル数が１の尤度関数 のページで、「サンプル数が複数の式は、サンプル数が１の式の積にならない場合」として分類した分布は、シンプルな式しか持っていないです。
シンプルな方の式も「尤度」として積極的に使う方法は、「サンプル数が複数の式は、サンプル数が１の式の積にならない場合」として、分類される分布の使い道になり、役に立ちそうです。
このページは、シンプルな尤度の式を理解を深めるために作ったものです。
「冗長」という表現では、あまり良い印象がないですが、サンプル１つずつの尤度関数の積のままでないと、できないこともあります。 それが、階層ベイズやベイズ更新です。
ベイズ統計 には、 階層ベイズ というアイディアがあります。
サンプル１つずつに対して、関数を作れていると、「母数はサンプル毎に異なり、母数も分布を持っている」というアイディアが使えるようになります。 ちなみに、このアイディアは、事前分布の有無とは関係がないので、ベイズ統計でなくても使えるようです。
ベイズ統計 には、ベイズ更新と呼ばれる 逐次学習 の方法があります。
新しいデータが得られた時に、 事後分布として求めたものを、新しい事前分布として使う方法です。
「In All Likelihood Statistical Modelling And Inference Using Likelihood」 Yudi Pawitan 著 Oxford University Press 2013
N=1の場合の、尤度関数の説明があります。
また、様々な分布の尤度関数が紹介されています。
順路
次は
ゼロ尤度関数
